 Die Überschriften a) bis d) verweisen auf die
vorhergehenden Seiten, f) bis h) auf nachfolgende Seiten:
Die Überschriften a) bis d) verweisen auf die
vorhergehenden Seiten, f) bis h) auf nachfolgende Seiten:| www.r-krell.de |
| Webangebot für Schule und Unterricht, Software, Fotovoltaik und mehr |
Willkommen/Übersicht > Informatik > Informatik mit Java, Seite e)
Teil e): Lineare Abstrakte Datentypen (Keller, Schlangen, Listen)
und einige Anwendungen (z.B. Tiefen- und Breitensuche)
 Die Überschriften a) bis d) verweisen auf die
vorhergehenden Seiten, f) bis h) auf nachfolgende Seiten:
Die Überschriften a) bis d) verweisen auf die
vorhergehenden Seiten, f) bis h) auf nachfolgende Seiten:
a) Grundlegendes zu Java, benötigte Software (inkl. Downloadadressen) und Installation
b) Erste Java-Programme (u.a. Autorennen u. Aufzug) sowie Verweise (Links) auf fremde Java-Seiten
c) Sortieren und Suchen in Java sowie grafische Oberflächen mit der Java-AWT
d) Adressbuch- und Fuhrpark-Verwaltung sowie Datei-Operationen mit Java
e) Lineare Abstrakte Datentypen (Keller, Schlangen, Listen) und einige Anwendungen (z.B. Tiefen- und Breitensuche)
f) Abstrakter Datentyp Baum ([binärer] Sortierbaum, Rechenbaum, Spielbaum)
g) Abstrakter Datentyp Graph (Adjazenzmatrix u. -listen, typische Fragestellungen, Tiefen- u. Breitensuche)
h) Bau eines Compilers Java -> 1_AMOR (Syntaxdiagramm, Scanner, Parser, Variablentabelle, Codeerzeuger)
Eine vollständige Übersicht aller Java-Seiten gibt's auf der Informatik-Hauptseite!
zum Seitenanfang / zum Seitenende
Die Adressbuch- und Fuhrparkverwaltung (siehe meine Java-Seite d)) oder ähnliche Beispiele machen deutlich, dass viele Computer-Anwendungen Daten ablegen und bei Bedarf wieder holen müssen. Es lohnt sich daher, grundsätzlich über geschickte Datenspeicherung nachzudenken.
Der Umgang mit Dateien hat gezeigt, dass es für die Programmiererin oder den Programmierer einer Anwendung keineswegs nötig ist, die technischen Einzelheiten der Datenspeicherung zu kennen: Wer Daten aus einer Hochsprache in eine Datei ablegt, muss sich nicht mit FAT- oder NTFS-Dateisystemen herumschlagen, Clustergrößen oder Besonderheiten von Disketten, Festplatten (HDD oder SSD), oder USB-Flash-Speichern kennen: Sie oder er schreibt einfach mit writeObject in einen FileOutputStream und liest bei Bedarf aus dem FileInputStream. Das heißt, es reicht eine abstrakte Vorstellung, wie in etwa eine Datei funktioniert (nämlich ähnlich wie eine Audiokassette, wo die Datensätze gleich Musik-Titeln irgendwie in einer Reihe hintereinander stehen und dass z.B. nach dem Lesen eines Datensatzes das Band, der Lesekopf oder der Dateizeiger oder was auch immer automatisch zum nächsten Datensatz weiter rückt, sodass beim nächsten Aufruf von readObject der nachfolgende Datensatz gelesen wird -- so wie beim Abspielen einer Kassette nach dem Hören eines Titels der nächste kommt). Dann braucht man nur noch ein paar Methoden (wie eben writeObject, readObject oder close), um mit dem Datenspeicher zu arbeiten.
Dabei haben Dateien gegenüber den bisher als Datenspeicher benutzten statischen Reihungen (Arrays) den Vorteil, dass sie dynamisch sind: Beim Anlegen muss man nicht angeben, wie groß die Datei wird. Sie belegt auf der Festplatte nur den Platz, den die tatsächlich abgelegten Datensätze benötigen. Andererseits ist der Dateizugriff relativ langsam und es nervt besonders, dass man aufwändig alle (anderen) Datensätze in eine neue Datei kopieren muss, wenn man nur einen Datensatz ändern will.
Ein besserer Datenspeicher wäre also vorzugsweise dynamisch und sollte das Hinzufügen oder Entfernen eines Datensatzes mit möglichst wenig Aufwand ermöglichen (am liebsten in jeweils nur einem Schritt und nicht abhängig von der Anzahl der bereits gespeicherten Daten).
Natürlich soll ein Datenspeicher anfangs leer sein, wenn er gerade neu erzeugt wurde. Weiterhin muss es möglich sein, Datensätze in den Speicher rein zu tun oder raus zu holen - wobei das Rausholen natürlich nur funktionieren kann, wenn (noch) Datensätze im Speicher sind und dieser nicht etwa leer ist. Und für viele Zwecke wäre es noch schön, wenn man sich auch mal einen Datensatz ansehen kann, ohne den Speicher zu verändern, also ohne den Datensatz ganz heraus holen und damit aus dem Speicher entfernen zu müssen. Mit diesen Forderungen haben wir den Datenspeicher schon soweit beschrieben, dass wir Methoden für die Bedienung des Speichers angeben können (oder - in objektorientierter Sprechweise - dass wir die Fähigkeiten des Speichers durch Methoden angeben können), die am einfachsten in einem Java-Interface vor- bzw. festgeschrieben werden [das vorangestellte E_ deutet auf die Zugehörigkeit zu dieser Java-Seite e) hin]:
|
public interface E_Speicher // legt nur fest, welche Methoden jeder Datenspeicher haben muss - Krell, 29.5.2004 - www.r-krell.de { public void rein (Object element); // packt das übergebene Element in den Speicher public boolean istLeer(); // sagt, ob der Speicher leer ist public Object zeige1(); // zeigt ein Element ohne Ändern des Speichers public Object raus(); // zeigt ein Element und löscht es aus dem
Speicher |
Dabei wird als Typ für einen Datensatz (hier Element genannt) vorstehend der allgemeinste Objekttyp Object benutzt, um das Speichern von Daten beliebiger Sorte zu ermöglichen. Im Jahr 2004, als das obige Interface E_Speicher geschrieben wurde, war das Stand der Technik - und ist auch heute noch in vielen Lehrplänen und Abituranforderungen so verankert. Deshalb habe ich die alte Beschreibung auch hier auf der Webseite gelassen (immer mit hellgrauem Untergrund).
Andererseits ist Java eigentlich eine typ-sichere Sprache. Man muss beim Programmieren den Typ jeder Variable, jeder Reihung und jeden Objekts
festlegen, damit der Compiler eine strenge Typprüfung vornehmen kann und Probleme zur Laufzeit vermieden werden. Natürlich soll trotzdem
die Bedienung des Datenspeichers z.B. mit rein undraus gleich erfolgen, egal was gespeichert wird. Seit der Java-Version 1.5
(auch Java 5 genannt) gibt es deshalb die Möglichkeit so genannter generischer Datentypen bzw. parametrisierter Datentypen, d.h. Klassen und
Interfaces, die eine Variable für den Typ der zu speichernden Daten enthalten. Die Variable wird erst später bei der Verwendung des
Interfaces oder beim Erzeugen eines Objekts durch einem konkreten Typ ersetzt. Damit ist sicher gestellt, dass im Speicher immer nur Elemente des
gleichen Typs gespeichert werden - wenn auch bei der Konstruktion des Speichers noch nicht bekannt sein muss, welcher das sein wird. Das Interface
erhält damit folgende bessere Gestalt (der Präfix P_ soll auf die Parametrisierung hinweisen; die generischen Quelltexte sind
immer weiß unterlegt):
|
public interface P_Speicher <Elementtyp> // hält fest, welche Methoden jeder Datenspeicher für Elemente vom (später festzulegenden) Elementtyp haben muss // Krell, 21.4.2015 - www.r-krell.de { public void rein (Elementtyp element); // packt das übergebene Element in den Speicher public boolean istLeer(); // sagt, ob der Speicher leer ist public Elementtyp zeige1(); // zeigt ein Element ohne Ändern des Speichers public Elementtyp raus(); //
zeigt ein Element und löscht es aus dem Speicher |
Sicherlich kann auch der E_Speicher von einem verantwortungsvollen Programmierer bzw. von einer aufmerksamen Programmiererin so verwendet werden, dass immer nur gleichartige Elemente in einen bestimmten Speicher gespeichert werden. Es könnten aber auch Elemente verschiedener Typen gespeichert werden - Java merkt das oben nicht und überlässt die Verantwortung dem Verwender, statt ihm - wie im Fall des P_Speichers - zu helfen.
Zum Schluss sei betont, dass zeige1 ein gespeichertes Element als Ergebniswert an die aufrufende Stelle zurück gibt und nichts wirklich auf dem Bildschirm anzeigt - dafür muss, sofern das überhaupt gewünscht ist, das Programm bzw. Objekt sorgen, das zeige1 oder raus benutzt.
Um die Entwurfs-Überlegungen und -Entscheidungen für solche Datenspeicher deutlich zu machen, erfolgt hier die eigene Entwicklung ohne Rückgriff auf ähnliche, in Java vordefinierte Modelle.
zum Seitenanfang / zum Seitenende
1. linearer abstrakter Datentyp: Keller
Oben wurde noch nicht festgelegt, welches Element gezeigt oder heraus geholt wird, wenn der Datenspeicher viele Elemente enthält und zeige1 oder raus aufgerufen werden. Eine einfache Organisation der Daten orientiert sich an käuflichen Speicherelementen für Parkmünzen, Pfefferminz-Tabletten oder an Warmhalte-Maschinen für Teller in einem Restaurant: Die Elemente sind in einer (oft vertikalen) Reihe linear angeordnet und jeweils die Münze, der Teller bzw. der Datensatz oder das Element, der/die/das als Letztes mit rein gespeichert wurde, ist oben zu sehen (d.h. würde von zeige1 genannt) und wird beim nächsten raus als Erstes wieder entfernt. Man spricht von einem LIFO-Speicher (LIFO = last in - first out), einem Stack, Stapel oder eben von einem Keller.
Die Funktionalität des Kellers - Zugriff nur an einem Ende; wie viele Teller und welche Teller in der Maschine stecken bzw. was außer dem obersten Element vielleicht sonst im Speicher ist, ist nicht zu sehen - kann durch so genannte Axiome bzw. durch die Forderung „keller.rein (x) => x = keller.raus();" (wobei das ausgekellerte Element oder Objekt x eben genau das vorher eingekellerte x sein soll) beschrieben werden.
Daraus lässt sich aber noch nicht ableiten, wie der Keller nun tatsächlich programmiert werden muss. Dafür gibt es nach wie vor verschiedene Möglichkeiten, die auch vor dem Anwender des Kellers versteckt gehalten werden sollen - schließlich soll der Benutzer des Kellers nur über die im Interface festgelegten Methoden auf den Keller zugreifen und sich ebensowenig Gedanken über dessen tatsächliche Realisierung machen müssen, wie oben der Benutzerin einer Datei FAT und Cluster egal waren. Auch dem Benutzer einer Küche ist das technische Innenleben z.B. eines Kühlschranks zu Recht egal: Hauptsache, dass Gerät kühlt, passt in das entsprechende Schrankelement der Einbauküche und lässt sich durch die Tür füllen oder leeren. Das Kühlaggregat ist irgendwo hinten versteckt und für den Kühlschrankbenutzer nicht erreichbar und braucht von ihm auch nicht verstanden werden. Wird der Kühlschrank einmal durch ein besseres, energiesparenderes Modell, das vielleicht auch weniger brummt, ersetzt, so soll der neue Kühlschrank in das selbe Loch der Einbauküche passen. Für den Benutzer darf sich nichts ändern: Er wird nach wie vor einfach die Tür aufmachen, um an gekühlte Lebensmittel zu kommen. Der Kühlschrank-Hersteller kann die gleiche Funktionalität aber auf unterschiedliche Weise einbauen - und in die Rolle eines Keller-Herstellers schlüpfen wir jetzt:
zum Seitenanfang / zum Seitenende
Keller - 1. Versuch: mit Reihung
Zunächst soll die vertraute Reihung zum Einsatz kommen - auch wenn deren Größe leider festgelegt werden muss, was eine
Obergrenze für die Anzahl der speicherbaren Elemente bedeutet. Man könnte das neueste Element immer in die Komponente mit dem Index 0 in
der Reihung schreiben (dann wäre zeige1 ganz einfach: man zeigt immer den Inhalt aus reihe[0]). Dieses Vorgehen hat aber den
Nachteil, dass man bei Einfügen eines weiteren Elements alle anderen Elemente jeweils um eine Position verschieben muss - das dauert und hat
nicht den oben erhofften 1-Schritt-Aufwand. Deshalb ist es besser, die Reihe von links nach rechts zu füllen und sich jeweils zu merken, wie
voll sie ist. Eine solche Möglichkeit wird jetzt gezeigt:
| public class E_Keller implements E_Speicher // 1. Versuch
2004: mit Reihung { // Alle Datenfelder leider nicht privat, damit später auch von der (vom // Keller abgeleiteten) Schlange aus der Zugriff möglich ist! final int MAX = 1000; // Maximale Elementzahl (statisch!) Object[] reihe; // Reihung als eigentliches Speicherelement int nr; // nr ist immer der Index das zuletzt eingefügten Elements, das // beim Keller auch das ist, das zuerst raus muss public E_Keller() { reihe = new Object[MAX]; // neue Reihung wird angelegt nr = -1; // Index -1 bedeutet leer! } public void rein (Object element) { nr = (nr + 1)%MAX; // modulo Max wegen später zu entwickelnder Schlange, reihe[nr] = element; //.. für den Keller reicht noch nr++ } public boolean istLeer() { return (nr == -1); // genau dann true, wenn nr == -1 ist. } public Object zeige1() { return (reihe[nr]); } public Object raus() { Object altesElement = reihe[nr]; nr--; return (altesElement); } } |
oder besser parametrisiert:
| public class P_Keller<ElTyp> implements E_Speicher<ElTyp> // 1. Versuch
2015: mit Reihung { final int MAX = 1000; // Maximale Elementzahl (statisch!) Object[] reihe; // Reihung als eigentliches Speicherelement; geht leider nicht als ElTyp[] reihe int nr; // nr ist immer der Index das zuletzt eingefügten Elements, das // beim Keller auch das ist, das zuerst raus muss public P_Keller() { reihe = new Object[MAX]; // neue Reihung wird angelegt nr = -1; // Index -1 bedeutet leer! } public void rein (ElTyp element) { nr = (nr + 1)%MAX; // modulo Max wegen später zu entwickelnder Schlange, reihe[nr] = element; //.. für den Keller reicht noch nr++ } public boolean istLeer() { return (nr == -1); // genau dann true, wenn nr == -1 ist. } public ElTyp zeige1() { return ((ElTyp)reihe[nr]); //mit Type-Casting auf den Elementtyp; nicht 100% sicher - führt zu Warnung } public ElTyp raus() { ElTyp altesElement = (ElTyp)reihe[nr]; nr--; return (altesElement); } } |
Alle Methoden haben 1-Schritt-Aufwand (ohne Schleifen!). Man veranschauliche sich mit einem Bleistifttest, wie hier durch Erhöhen oder Erniedrigen von nr vor Eintrag bzw. nach Entfernen eines Elements aus der reihe tatsächlich den Kelleranforderungen entsprochen wird. Außerdem liegt es in der Verantwortung des Benutzers, vor der Verwendung von zeige1 oder raus den Keller mit istLeer zu prüfen, ob die gewünschten Operationen überhaupt möglich sind. Eine automatische Fehlerkontrolle oder -behandlung wurde hier nicht vorgesehen.
zum Seitenanfang / zum Seitenende
Keller - Ein erster Praxis-Test
Um den Keller auszutesten, könnte ein kleines Programm nach folgendem Bauplan geschrieben und gestartet werden:
| public class E_KellerTest //Krell, 29.5.2004 -- www.r-krell.de { public void führeAus() { E_Keller keller = new E_Keller(); System.out.println("Ist der neu erzeugte Keller leer? "+ keller.istLeer()); keller.rein ("Das");keller.rein ("ist"); keller.rein ("ein"); keller.rein ("Test"); System.out.println(keller.zeige1()); while (! keller.istLeer()) { System.out.println(keller.raus()); } } public static void main (String[] s) { E_KellerTest testObjekt = new E_KellerTest(); testObjekt.führeAus(); } } |
| public class P_KellerTest //Krell, 21.4.2015 -- www.r-krell.de { public void führeAus() { P_Keller<String> keller = new P_Keller<String>(); // es wird ein Keller für Strings angelegt! System.out.println("Ist der neu erzeugte Keller leer? "+ keller.istLeer()); keller.rein ("Das");keller.rein ("ist"); keller.rein ("ein"); keller.rein ("Test"); System.out.println(keller.zeige1()); while (! keller.istLeer()) { System.out.println(keller.raus()); } } public static void main (String[] s) { P_KellerTest testObjekt = new P_KellerTest(); testObjekt.führeAus(); } } |
Erwartungsgemäß funktioniert unser Keller und liefert folgende Ausgabe:
zum Seitenanfang / zum Seitenende
Keller - 2. Versuch: mit rekursiven Knoten
Nach außen ist der vorstehende Keller schon voll funktionsfähig, aber die Verwendung der statischen Reihung mit Platz für 1000
Objekte ist noch nicht ganz optimal. Eine dynamische Struktur mit rekursiven Knoten (hier in Minimalausstattung) kann helfen:
| public class E_Knoten //Krell, 29.5.2004 -- www.r-krell.de { Object inhalt; E_Knoten zeiger; // rekursive Definition: zeiger ist ein gleichartiger Knoten // bzw. ein Verweis auf einen anderen Knoten vom hier definierten Typ //natürlich wären private Datenfelder mit Zugriffsmethoden "schöner" } |
bzw. parametrisiert:
| public class P_Knoten
<ElTyp> //Krell, 21.4.2015 -- www.r-krell.de { ElTyp inhalt; P_Knoten<ElTyp> zeiger; // rekursive Definition: zeiger ist ein gleichartiger Knoten // bzw. ein Verweis auf einen anderen Knoten vom hier definierten Typ //natürlich wären private Datenfelder mit Zugriffsmethoden "schöner" } |
Mehrere dieser Knoten können eine Speicherstruktur bilden (aus anderen Programmiersprachen als Zeigerstruktur bekannt), die man sich am besten grafisch veranschaulicht:
Damit ergibt sich dann folgender Programmtext für die zweite, bessere (weil dynamische) Keller-Implementation:
| public class E_Keller implements E_Speicher //Krell, 29.5.2004 -- www.r-krell.de { E_Knoten kopf; // Verankerung der Struktur. Nicht privat, damit vererbbar public E_Keller () { kopf = null; } public boolean istLeer() { return (kopf == null); } public Object zeige1() { return (kopf.inhalt); } public Object raus() { Object altesElement = kopf.inhalt; kopf = kopf.zeiger; return (altesElement); } public void rein (Object neuesElement) { E_Knoten neu = new E_Knoten(); // mit einem passenden Konstruktor in E_Knoten neu.inhalt = neuesElement; // ließen sich diese Zeilen natürlich neu.zeiger = kopf; // eleganter zusammenfassen kopf = neu; } } |
und in der besseren, parametrisierten Form:
| public class P_Keller<Elementtyp> implements P_Speicher<Elementtyp> //Krell, 21.4.2015 -- www.r-krell.de { P_Knoten<Elementtyp> kopf; // Verankerung der Struktur. Nicht privat, damit vererbbar public P_Keller () { kopf = null; } public boolean istLeer() { return (kopf == null); } public <Elementtyp> zeige1() { return (kopf.inhalt); } public <Elementtyp> raus() { <Elementtyp> altesElement = kopf.inhalt; kopf = kopf.zeiger; return (altesElement); } public void rein (<Elementtyp> neuesElement) { P_Knoten<Elementtyp> neu = new P_Knoten<Elementtyp>(); // mit einem passenden Konstruktor in P_Knoten neu.inhalt = neuesElement; // ließen sich diese Zeilen natürlich neu.zeiger = kopf; // eleganter zusammenfassen kopf = neu; } } |
Natürlich verläuft auch hier der Praxis-Test ebenso erfolgreich wie oben beschrieben - für den Benutzer (z.B. für ein Objekt von KellerTest) ändert sich beim Austausch der Keller nichts (so, wie sich für den Küchenbenutzer der Kühlschrank-Austausch nicht grundsätzlich bemerkbar macht).
zum Seitenanfang / zum Seitenende
2. linearer abstrakter Datentyp: Schlange
Obwohl es viele schöne Anwendungen für Keller gibt, so trifft man - z.B. in der Warteschlange vor der Supermarktkasse - auch auf Situationen, wo besser das Element zuerst raus kommt, das als Erstes gespeichert wurde (bzw. die Person dran kommt, die schon am längsten in der Schlange steht). Hier immer den zuletzt Gekommenen zuerst abzufertigen, würde sicher für einigen Unmut sorgen. rein und raus sollen also auf die verschiedenen Enden der linearen Struktur wirken. Weiterhin soll es keinen Zugriff auf Elemente mitten in der Schlange geben; Vordrängeln o.ä. ist strikt verboten. Eine passende Struktur heißt FIFO-Speicher (FIFO = first in - first out), Queue oder eben Schlange.
Gegenüber dem Keller muss nur eine der beiden Operationen, rein oder raus, so geändert werden, dass sie jetzt auf das andere Ende der Liste verketteter Knoten wirkt. Da - wie oben erläutert - für raus die Pfeil-/Verkettungsrichtung wichtiger ist, ist es leichter, rein auf das andere Ende wirken zu lassen, das damit zum hinteren Ende der Schlange wird (wo man sich anstellen muss und so in die Schlange rein kommt: „Hinten anstellen, bitte!"). Um dieses hintere Ende immer rasch erreichen zu können (ohne jeweils die ganze Speicherkette vom Kopf bis ganz hinten durchgehen zu müssen), bietet sich als Attribut ein weiteres klassenglobales Datenfeld (Attribut) schwanz an, das den letzten Knoten aufnimmt (sprich: auf den letzten [=jüngsten] Knoten zeigt). kopf zeigt weiterhin auf das vordere Ende, wo man an der Kasse dran kommt und dann mit dem bezahlten Einkauf die Schlange verlassen kann.
Da nur schwanz dazu kommt und nur die Methode rein verändert werden
muss, ist die Klassen-Vererbung möglich - hier gezeigt an der dynamischen Implementation mit Knoten: Die Schlange erbt alles vom Keller (in
der 2. Version), fügt den schwanz dazu und überschreibt das bisherige rein mit einer eigenen, gleichnamigen aber
inhaltlich abgewandelten Methode (für das hintere Ende)
| public class E_Schlange extends E_Keller // erweitert den Keller zur Schlange (dynamische Implementation mit Knoten) -- Krell, 29.5.04 { E_Knoten schwanz; // kopf existiert schon im und durch den Keller public E_Schlange () { super(); // Keller-Konstruktor aufrufen schwanz = null; // zusätzlich } public void rein (Object neuesElement) // wirkt jetzt am Ende { E_Knoten neu = new E_Knoten (); neu.inhalt = neuesElement; neu.zeiger = null; // letztes Element immer ohne Nachfolger if (istLeer()) { kopf = neu; //bisher 1. Element: auch kopf muss auf den neuen Knoten zeigen } else { schwanz.zeiger = neu; //sonst: Vorgänger muss auf den neuen Knoten zeigen } schwanz = neu; //immer zeigt auch der Schwanz auf den letzten Knoten } } |
Auch wenn die Vererbung bequem dafür sorgt, dass die drei Methoden, die bei Keller und Schlange genau übereinstimmen (nämlich ist_Leer, zeige1 und raus) nicht nochmal geschrieben werden müssen, ist sie hier von der Sache her fragwürdig: Schließlich ist die Schlange keine Spezialisierung oder erweiterte Form eines Kellers, sondern ein anderer, gleichwertiger Datenspeicher. Insofern soll in der neuen, parametrisierten Fassung eine gemeinsame Oberklasse über sowohl dem Keller als auch der Schlange stehen. Die Speicherstrukturen erben beide davon, aber nicht untereinander. Anstatt den Quelltext hier einzufügen, zeige ich lieber eine entsprechende Zusammenfassung aus meinem Unterricht vom Februar 2015, zumal dort unter Punkt 6 auch die Verwendung der Datenstrukturen mit verschiedenen Typen exemplarisch vorgestellt wird. Allerdings werden statt kopf und schwanz die Namen vorne und hinten für die Verankerung der Speicherstrukturen verwendet:
Zum Test der alten E_Schlange kann der oben (pfirsichfarben unterlegte) KellerTest so abgeändert werden, dass überall Keller durch Schlange ersetzt wird. Die Ausgabe sollte sich natürlich ändern, nämlich wie?
Leider kann das Testprogramm nicht einfach auf E_Speicher (bzw. P_Speicher) abgeändert werden, und damit gleichermaßen und unverändert für Keller und Schlange verwendbar sein. Zwar stehen alle auftretenden Methoden schon in E_Speicher, aber noch ohne Inhalt. Und von einem Interface kann - anders als von einer Klasse - kein neues Objekt etwa mit E_Speicher allgemein = new E_Speicher(); erzeugt werden. Außerdem wüsste das TestObjekt dann auch nicht, welche der beiden rein-Methoden es verwenden muss, die vom Keller oder die von der Schlange (bzw. gar keine, weil in E_Speicher ja noch gar kein Rumpf angegeben ist) („Polymorphie"). Da Java die späte Bindung erlaubt, ist trotzdem eine Verallgemeinerung möglich, sofern man beim Aufruf von führeAus durch Übergabe eines geeigneten Parameters wie 'k' oder 's' dafür sorgt, dass der noch als allgemeines E_Speicher-Objekt definierte speicher zumindest beim Erzeugen ein konkretes Objekt von einer der beiden richtigen Klassen wird. Die Erzeugung kann auch außerhalb von führeAus erfolgen, sofern E_Speicher speicher; auch außerhalb als globales Datenfeld definiert wurde. Java, das beim Compilieren des Programms noch nicht weiß, mit welchem Parameter führeAus aufgerufen wird, arbeitet trotzdem beim Aufruf zur Laufzeit mit der passenden Methode entweder für den Keller oder die Schlange - je nachdem, als was speicher erzeugt wird!
public void führeAus (char wahl) // wahl z.B. aus Kommandozeilenparametern von main { E_Speicher speicher; if (wahl == 'k') { speicher = new E_Keller(); } else { speicher = new E_Schlange(); } System.out.println ("Ist der neu erzeugte Speicher leer? "+ speicher.istLeer()); speicher.rein ("Das"); speicher.rein ("ist"); speicher.rein ("ein"); speicher.rein ("Test"); System.out.println (speicher.zeige()); while (! speicher.istLeer()) { System.out.println (speicher.raus()); } } |
Eine andere, interaktive Möglichkeit zum Testen vom Keller und Schlange in der alten, nicht-parametrisierten Form gibt's mit einem Java-Applet auf einer Sonderseite:
Interaktiver Test von (altem) Keller und Schlange mit einem Java-Applet
Und die Quelltexte einer entsprechenden Oberfläche für den parametrisierten Keller und die parametrisierte Schlange (mit gemeinsamem Vorfahr) können hier herunter geladen und ausprobiert werden. Beispielhaft kann man wählen, ob die Speicher Kommazahlen oder Texte aufnehmen sollen. Als Typ-Parameter dürfen dabei übrigens keine primitiven Typen verwendet werden, sondern es müssen gegebenenfalls die Wrapper-Klasse (also Integer statt int, Double statt double usw.) benutzt werden. Seit Java bei Bedarf automatisch primitive Typen in Objekte der Wrapper-Klasse umwandelt und ausgekellerte Objekte auch problemlos als primitive Typen verwendet (Auto-Boxing bzw. -Unboxing), ist damit keinerlei programmtechnischer Mehraufwand verbunden.
zum Seitenanfang / zum Seitenende
Referat über Keller und Schlangen
Ursprünglich für eine Lehrerfortbildungsveranstaltung geschrieben, habe ich das oben skizzierte alte Konzept von Keller und Schlange 2006 nochmal ausführlicher notiert. Und als Folge der an meinen Vortrag anschließenden Diskussion habe ich noch zwei alternative Varianten ausprobiert und dargestellt, nämlich Keller und Schlange als gleichberechtigte Erben von einer gemeinsamen abstrakten Oberklasse sowie die - erst ab der Java-Version (1.)5 mögliche - Typisierung so genannter generischer Keller und Schlangen (wie beides oben inzwischen schon dargestellt wurde). Das Referat gibt's entweder als pdf-Datei zum Online-Lesen in neuem Fenster
Referat Keller-und-Schlange.pdf (39 Seiten, 560 kB)
oder - gemeinsam mit den Quelltexten der vorgestellten Java-Programme - zum Download in einer Archiv-Datei: keller-und-schlange.zip (335 kB).
zum Seitenanfang / zum Seitenende
Wegsuche im Labyrinth
- eine nichttrivale Verwendung von Keller oder Schlange bei der Tiefen- bzw. Breitensuche
 Das oben vorgestellte Testprogramm, egal
ob konkret oder mit später Bindung, ist recht einfach und macht die Notwendigkeit eines Kellers oder eine Schlange nicht sehr deutlich. Dazu
bedarf es anderer, zum Teil schon angedeuteter Beispiele aus dem Alltag. Die Vorteile abstrakter Datentypen wie Keller oder Schlange werden
natürlich nur augenfällig, wenn sich die gleichen Strukturen in einer Vielzahl verschiedener Anwendungen unverändert verwenden
lassen. Hier sind der Unterricht und auch die Fantasie der Schülerinnen und Schüler gefordert.
Das oben vorgestellte Testprogramm, egal
ob konkret oder mit später Bindung, ist recht einfach und macht die Notwendigkeit eines Kellers oder eine Schlange nicht sehr deutlich. Dazu
bedarf es anderer, zum Teil schon angedeuteter Beispiele aus dem Alltag. Die Vorteile abstrakter Datentypen wie Keller oder Schlange werden
natürlich nur augenfällig, wenn sich die gleichen Strukturen in einer Vielzahl verschiedener Anwendungen unverändert verwenden
lassen. Hier sind der Unterricht und auch die Fantasie der Schülerinnen und Schüler gefordert.
Aus der Fülle möglicher Anwendungen sei hier die Wegsuche in einem Labyrinth heraus gegriffen. In einem zufällig erzeugten Labyrinth soll ein Weg von S (Start) nach Z (Ziel) gefunden werden. Da S und Z auch von freien Feldern umgeben sein können, versagen Verfahren wie „immer mit der rechten Hand an der Wand entlang". Nach längerer Überlegung, für die man im Unterricht aus ausreichend Zeit einräumen muss, kann möglicherweise folgendes Verfahren entwickelt werden:
zum Seitenanfang / zum Seitenende
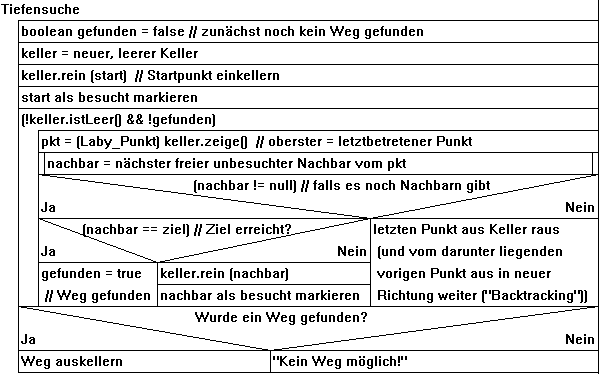
Tiefensuche (mit Keller)
Vom dem Kästchen oder Punkt, auf dem man sich gerade befindet (anfangs also dem Startpunkt S), sucht man - am besten nach einem festen
Schema, in dem man z.B. der Reihe nach den östlichen, nördlichen, westlichen und schließlich südlichen Nachbarn ausprobiert -
einen freien, bisher noch unbesuchten Nachbarn. Dort geht man hin, speichert die Koordinaten vorsorglich im Keller, und verfährt von dort aus
ebenso, d.h. sucht wieder einen freien Nachbarn, um dorthin weiter zu gehen, usw. Erreicht man auf diese Weise das Ziel, ist alles bestens.
Gerät man in eine Sackgasse (erkennbar daran, dass es keinen freien unbesuchten Nachbarn mehr gibt), so zieht man sich Schritt für
Schritt aus der Sackgasse zurück und probiert es vom jeweiligen Vorgängerpunkt (den man zum Glück im Keller findet) mit einem
anderen, hoffentlich besseren unbesuchten Nachbarn.

zum Seitenanfang / zum Seitenende
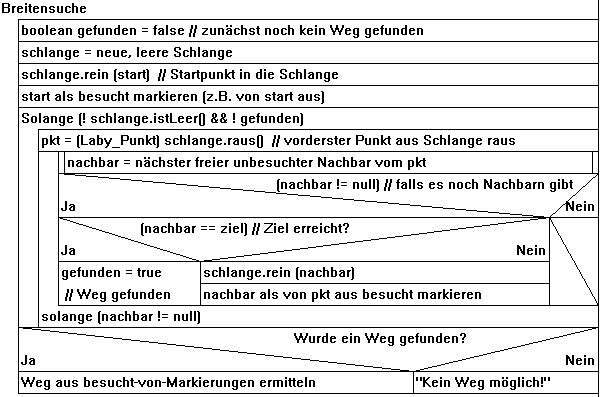
Breitensuche (mit Schlange)
Die Tiefensuche findet nicht immer den schnellsten Weg. Das motiviert zur Suche nach besseren Suchmethoden. Vermutlich nur mit Hilfe lässt sich folgende Strategie entwickeln, die sich außerhalb des Computers nur für riesige Pfadfinder-Gruppen eignet: Die ganze Gruppe startet beim Startpunkt S. Bei diesem und bei jedem folgenden Punkt wird immer nach dem gleichen Verfahren vorgegangen: gibt es mehrere unbesuchte Nachbarn, teilt sich die Gruppe und jeder Nachbar wird von einem Teil der Pfadfinder besucht (dafür müssen immer noch genügend Gruppenmitglieder zur Verfügung stehen). Erreicht endlich irgendein Pfadfinder das Ziel, ruft er ganz laut und die Suche stoppt. Vom Rufer (am Ziel) lässt sich jetzt der Weg zum Startpunkt zurück verfolgen und ausgeben. Die Grafik zeigt, dass natürlich abseits des Weges auch noch viele Sucher unterwegs waren (alle vom Start aus betretenen Punkte wurden mit a, alle von einem a-Punkt aus erreichten Punkte wurden mit b bezeichnet usw.). Es gibt aber keine kürzeren Wege (= mit weniger Zwischenpunkten) als den gefundenen!

Interaktiver Test der Wegsuchen im Labyrinth (mit Java-Applet)
zum Seitenanfang / zum Seitenende
3. linearer abstrakter Datentyp: Liste
Für viele Anwendungen ist es doch eine starke Einschränkung, wenn man wie bei Keller und Schlange nur an die Datensätze am vorderen oder hinteren Ende des Speichers heran kommt. Sicher könnte man den Keller oder die Schlange vorübergehend teilweise in einen Zwischenspeicher (am liebsten natürlich wieder in einen linearen ADT) entleeren, bis man das gesuchte Element oder eine passende Einfügestelle gefunden hat. Aber dann muss viel kopiert werden, steigt der Aufwand und ein Zugriff ist nicht mehr unabhängig von der Anzahl der gespeicherten Elemente in immer nur einem Schritt zu realisieren. Also wird nun ein Datenspeicher gesucht, der zwar auch wieder linear organisiert und dynamisch ist, aber wo man trotzdem an jeder beliebigen Stelle in (oder vor oder hinter) der Kette der vorhandenen Elemente mit rein ein neues Element einfügen kann, oder wo man sich jedes beliebige Element mit zeige1 ansehen oder es mit raus löschen kann (sofern die Liste nicht leer ist). Neben den ganz oben im Interface E_Speicher bzw. P_Speicher schon festgelegten Methoden muss es dazu noch weitere Methoden zur Auswahl der richtigen Stelle oder des richtigen Elements geben.
Bei der einfachen Liste lehnt man sich dabei an die Möglichkeiten von Dateien an (vgl. meine Java-Seite d) bzw. den Tonband-Vergleich oben im ersten Abschnitt „Abstrakter Datentyp (ADT) - Motivation und Anforderungen" auf dieser Seite e)). Auch der Vergleich mit einem Aktenordner ist hilfreich, wenn man die Datensätze als eingeheftete, nur einseitig beschriebene Blätter auffasst, das aktuelle Element immer nur das gerade aufgeschlagene Blatt ist und man immer nur genau eine Seite weiter blättern darf - es sei denn, man geht mit einem Schlag per anDenAnfang in die Ausgangsstellung zurück, sodass (wieder) die erste Seite oben und aktuell ist. Wie im richtigen Aktenordner wird eingeheftet bzw. eingefügt immer direkt vor der aktuell aufgeblätterten Seite..
Man kann
Es ist nicht möglich, beim Weg nach hinten durch die Liste Datensätze zu überspringen oder sich - in umgekehrter Richtung - um
einen einzelnen Datensatz nach vorne zu bewegen. Die einzige Möglichkeit, nach vorne zu kommen, besteht in der Verwendung von
anDenAnfang, was aber immer direkt nach ganz vorne führt. Mit diesen beiden Methoden, anDenAnfang und weiter, kann
man trotzdem jeden Datensatz der Liste erreichen und ihn dadurch zum aktuellen Datensatz erklären.
Außerdem muss es möglich sein, im Aktenordner die letzte Seite umzulegen und auf den leeren hinteren Aktendeckel zu starren, damit
hinter der bisher letzten Seite noch ein neues Blatt eingefügt werden kann. Entsprechend muss weiter die aktuelle Position sogar bis
hinter das letzte Element verschieben können!
rein könnte wahlweise das aktuelle Element ersetzen (was nicht klug wäre, wenn man ein neues Element nur aufnehmen kann, wenn man dabei ein altes löscht. So bekommt man eine Liste nie wirklich voller) oder rein könnte vor oder hinter dem aktuellen Element das neue Element einfügen. Hält man sich vor Augen, dass man später die einfache Liste vielleicht einmal zu einer sortierten Liste erweitern will - also z.B. einen neuen Schüler an die passende Stelle in eine nach Nachnamen alphabetisch sortierte Klassenliste aufnehmen will - so hat das Einfügen vor dem aktuellen Element unschätzbare Vorzüge: Um die richtige Stelle z.B. für „Müller" zu finden, muss man (jedenfalls wenn die gerade aufgeschlagene, aktuelle Stelle etwa bei/mit „Schulze" schon hinter der Einfügestelle ist) mit anDenAnfang nach ganz vorne, um etwa bei „Aksu" anzufangen. Wenn man dann mit weiter und zeige1 „Bevic" liest, weiß man noch nicht, ob man „Müller" schon einfügen kann. Vielleicht kommen noch „Krause" und „Lehmann". Man muss also weiter und weiter gehen (und sich jedes Element zeigen lassen). Erst wenn man etwa nach „Meier" endlich auf „Ngyen" trifft, weiß man, dass man dazwischen „Müller" einfügen muss(te). Inzwischen ist „Meier" aber nicht mehr aktuell, sondern „Ngyen" ist aktuell (sonst hätte man „Ngyen" nicht mit zeige1 lesen können). Zurück zu „Meier" ist nicht mehr möglich - in der Liste gib's kein Zurück, s.o.! Also kann auch nicht mehr mit einem Befehl wie Nach „Meier" eingefügt werden, weil das Programm „Meier" nicht mehr kennt bzw. erreicht. Wird aber mir rein vorm aktuellen Element eingefügt, dann stört es nicht, dass „Ngyen" schon aktuell ist - im Gegenteil: „Müller" kommt mit Vor „Ngyen" dann nämlich genau an die richtige Stelle!
Damit man dann aber auch noch einen Namen wie „Zafiris" ganz hinten an die Liste anfügen kann, muss man aktuell praktisch noch hinter das letzte Element setzen können (s.o.: auf den hinteren Aktendeckel). Diese Positionierung des Auswahlzeigers soll dann durch das Ergebnis true der Kontrollmethode istAmEnde (bzw. besser istHintermLetzten) überprüfbar werden, weil man dort kein aktuelles Element mehr zeigen oder raus nehmen kann, d.h.
Solche Überlegungen - wie man einen Datenspeicher am besten organisiert und welche Methoden nötig sind, um alle Zugriffe mit wenig
Aufwand durchführen zu können -- machen übrigens einen wichtigen Teil der Informatik aus und sind völlig unabhängig von
der verwendeten Programmiersprache. Durchdachte Entwürfe zeichnen die Meisterin oder den Meister des Faches aus. Schlechte Entwürfe und
Konzeptionen führen auch dann nicht zu guten Implementationen, wenn die schlechten Zugriffe mit schnellen Algorithmen programmiert werden.
Meist paaren sich allerdings globale Entwurfdefizite mit Detailverliebtheit und Effekthascherei: an Stelle sicherer und schneller Methoden werden
manche Funktionen mit peppigen, aber wenig sinnvollen Zusätzen unnötig aufgebläht, weil die Programmierer mit bombastischen
Programmiertricks brillieren wollen.
Auch bei den Vorgaben zum Zentralabitur 2014-2016 wurde offenbar leider vorher weniger überlegt, sodass 3 verschiedene rein-Methoden
eingeführt werden mussten, damit man an allen Stellen einfügen kann. Algorithmen bzw. eine konkrete Implementation wurden nicht
mitgeliefert (s.u.).
Aber zurück zur Liste: Diese soll hier wieder mit einer Kette aus rekursiven Knoten realisiert werden, wobei jeder Knoten genau ein Element
beliebigen (Objekt-bzw. zur Laufzeit festzulegenden Element-)Typs als Inhalt aufnimmt (ähnlich wie oben die grün unterlegte Kette beim 2.
Keller). Die Knoten sind also wieder Objekte von der schon angegebenen Klasse E_Knoten bzw. P_Knoten. Fügt man in eine
solche Kette ein Element ein, muss man - obwohl das Element rechts neben der Einfügestelle das aktuelle ist - trotzdem den zeiger des
Knotens links davor ändern, nämlich auf den neuen Knoten richten (mit dem neuen Element als Inhalt). Hat man also nur einen Hilfszeiger
auf den aktuellen Knoten, kommt man an den linken Knoten (gegen die Pfeilrichtung der Verkettung) nicht dran - es sei denn, durch mühsames
Durchgehen der ganzen Kette wieder von ganz vorne. Also ist es besser, einen Hilfszeiger voraktuell (oder vorAktuell in meiner
neueren Implementation) auf das Knoten links vom aktuellen zu setzen, weil man dort bei rein, aber auch bei raus, arbeiten muss,
in dem man dort den zeiger verbiegt. Da man für zeige1 bequem vom voraktuellen Knoten in einem Schritt nach rechts zum
aktuellen Knoten mit dem gesuchten Inhalt kommt, ist ein Hilfszeiger auf den aktuellen Knoten gar nicht nötig. Das erleichtert dann das
Aktuellmachen hinter dem letzten Element, weil man keinen Zeiger ins Leere setzen muss, sondern einfach den letzten Knoten mit voraktuell
referenziert.
Andererseits entstehen jetzt Probleme, wenn man den ersten Knoten ganz links aktuell machen will (nämlich mit anDenAnfang):
voraktuell müsste noch links davon irgendwo hin zeigen. Dann kann man aber nicht mit voraktuell.zeiger zum ersten Knoten
gelangen (wenn es den Knoten voraktuell nicht gibt, kann er auch keinen zeiger haben). Entweder sind aufwändige
Fallunterscheidung mit vielen if-Anweisungen in den Methoden nötig, oder man klebt einfach links an die Liste noch einen
zusätzlichen Knoten vor den Knoten mit dem ersten Element davor. Der Inhalt dieses zusätzlichen Knotens ist egal, wir brauchen nur seinen
zeiger. Man spricht daher von einem dummy-Knoten (oder ungenauer auch von einem dummy-Element) wegen dummy =
leer, taub.
| public class E_Liste //Krell, 29.5.2004 -- www.r-krell.de { E_Knoten dummy, voraktuell; //statt "dummy" wird später auch der Name "vorAnfang" verwendet, //statt "voraktuell" wird der Zeiger später "vorAktuell" genannt. public E_Liste() //Konstruktor { dummy=new E_Knoten(); dummy.zeiger=null; voraktuell=dummy; } public void anDenAnfang() //erstes echtes Element wird aktuell { voraktuell=dummy; } public void rein(Object neuerInhalt) { //Es wird vor dem aktuellem Element E_Knoten neu=new E_Knoten(); //das neue eingefügt neu.inhalt=neuerInhalt; neu.zeiger=voraktuell.zeiger; voraktuell.zeiger=neu; weiter(); //das bisherige aktuelle Element bleibt aktuell } public Object zeige1() //zeigt aktuelles Element { return (voraktuell.zeiger.inhalt); } public void weiter() //macht Nachfolger des aktuellen Elements aktuell { voraktuell=voraktuell.zeiger; } public boolean istAmEnde() //Abfrage, ob aktuell schon hinterm letzten Element steht. { //Wenn true, kein zeige1 oder raus mehr möglich, ... return (voraktuell.zeiger==null); //.. aber noch rein, um ein neues Element } //ganz hinten anzufügen! public Object raus() //nimmt das aktuelle Element heraus { //Nachfolger des entfernten Elements wird aktuell Object hilf=voraktuell.zeiger.inhalt; voraktuell.zeiger=voraktuell.zeiger.zeiger; return(hilf); } public boolean istLeer() //Abfrage ob Liste leer ist, d.h. außer { //dem Dummy-El. gar keine Elemente enthält return(dummy.zeiger==null); } } |
und in typisierter bzw. parametrisierter Form (jetzt mal mit einem verbesserten Knoten mit Konstruktor)
| public class P_Knoten
<Elementtyp> // R. Krell, im März 2015 -- www.r-krell.de { Elementtyp inhalt; // hierhin kommt das gespeicherte Element P_Knoten<Elementtyp> zeiger; // hier merkt man sich den Knoten mit dem nächsten Element public P_Knoten (Elementtyp i, P_Knoten<Elementtyp> z) { inhalt = i; zeiger = z; } } |
| // parametrisierte Liste -- für IF Q1 M - R. Krell, März 2015 (www.r-krell.de) public class P_Liste <ElTyp> { P_Knoten<ElTyp> vorAnfang = new P_Knoten<ElTyp> (null, null); // (bei E_Liste: dummy) P_Knoten<ElTyp> vorAktuell = vorAnfang; public void rein (ElTyp neuesEl) // füllt neues Element vor aktuellem ein { P_Knoten<ElTyp> neuerKn = new P_Knoten<ElTyp> (neuesEl, vorAktuell.zeiger); vorAktuell.zeiger = neuerKn; vorAktuell = neuerKn; // damit bisheriger aktueller Knoten, //vor dem gerade neuerKn eingefügt wurde, weiter aktuell ist } public boolean istLeer() // wird genau dann true, wenn die Liste leer ist { return (vorAnfang.zeiger == null); } public ElTyp zeige1() // zeigt das aktuelle Element (bei E_Liste: zeige()) { return vorAktuell.zeiger.inhalt; } public ElTyp raus() // löscht (und zeigt) aktuelles Element; Nachfolger wird aktuell { ElTyp element = vorAktuell.zeiger.inhalt; vorAktuell.zeiger = vorAktuell.zeiger.zeiger; return (element); } public void anDenAnfang() // macht erstes Element aktuell { vorAktuell = vorAnfang; } public boolean istHintermLetzten() // true, wenn aktuelle Position hinterm Listenende { // (bei E_Liste: istAmEnde()) return (vorAktuell.zeiger == null); } public void weiter() // macht nächstes Element aktuell (Nachfolger vom aktuellen) { vorAktuell = vorAktuell.zeiger; } } |
Zum Testen der neuen, typisierten Liste stelle ich wieder ein Applet bereit, das zur Laufzeit die Wahl des Elementtyps zulässt. Applet und vollständiger Quelltext sowie die Möglichkeit zum Herunterladen der ausführbaren .jar-Datei finden sich auf der Extra-Seite
Demonstration der (parametrisierten) Liste mit interaktivem Applet
zum Seitenanfang / zum Seitenende
Implementation der (alten) ADTs in Java...
Die hier vorgestellten linearen abstrakten Datentypen 1 bis 3 (Keller bis Liste) sind natürlich so universell verwendbar und auch in ähnlicher Weise in vielen Informatikbüchern beschrieben, dass vergleichbare Implementationen auch mit der Java-JDK bzw. -SDK als Bibliotheksklassen mitgeliefert werden, nämlich u.a. Stack, Vector, ArrayList und LinkedList.
Eine Übersicht über dort verwendete Namen und Methoden und ihren exemplarischen Gebrauch zeigt mein schon etwas älteres kommentiertes Testprogramm auf einer Sonderseite (allerdings noch ohne die neuen Datenstrukturen, die mit/seit Java 5 mitgeliefert werden):
Beispiele älterer mit Java mitgelieferter linearer abstrakter Datentypen
.. und der neuen parametrisierten ADTs auf meinen Webseiten
Bei den Informatik-Klausuren aus/ab 2013 werden typisierte Datentypen in Materialien zum Download angeboten und kommen in den Aufgaben (und Lösungen) vor. Außerdem wird auf der Seite SWE-2 zum Softwareengineering bei der Projektarbeit ein Kartenspiel vorgestellt, das eine für Spielkarten typisierte Schlange nutzt. Und natürlich sind die von Java mitgelieferten Datentypen - anders als bei den älteren Beispielen noch dargestellt - inzwischen auch alle typisierbar!
Meine Informatik-Klausuren und -Materialien sowie
dort u.a. Quelltexte und Bilder Q1_Keller&Schlange.zip (260 kB)
zurück zum Abschnitt Referat über Keller und Schlangen auf dieser Seite (in der pdf-Datei den Anhang
beachten!)
Meine Software-Engineering-Seite SWE-2 mit dem Kartenspiel
Rot&Schwarz (Applet einschl. Quelltext)
Schließlich hat auch in anderem Zusammenhang - nämlich beim Sortieren in Reihungen - ganz unten auf meiner Seite c) Sortieren und Suchen die Typisierung ebenfalls Einzug gehalten (und nennt einen Trick, der auch hier verwendbar ist
zum Seitenanfang / zum Seitenende
Implementation der ADTs laut Abitur-Vorgaben 2014 bis 2016
Da die abstrakten Datentypen Unterrichtsthema der Oberstufe sind und sowohl im Gymnasium als auch im Technischen oder Beruflichen Gymnasium bzw. Berufskolleg im Abitur vorkommen können, wurden in (Anlagen zu) Lehrplänen oder Abitur-Vorgaben die Methodennamen und ihre Funktion festgeschrieben. Die Datentypen werden noch nicht in der generischen, d.h. parametrisierten bzw. typsicheren Form verlangt. Im Gymnasium in Nordrhein-Westfalen haben die Beschreibungen speziell des Datentyps Liste eine wechselvolle Geschichte: in den ersten Jahren des Zentralabiturs konnte man mit den beschriebenen Methoden gar nicht an allen Stellen der Liste einfügen. Zudem war der Sprachstil deutlich von Pascal bzw. Delphi geprägt. Später wurde mehrfach nachgebessert, sodass inzwischen "alles geht", allerdings eine ziemliche Flickschusterei entstanden ist. Dazu kommt, dass - anders als bei mir oben - versucht wurde, manche Methoden fehlertolerant zu machen (sodass z.B. beim Versuch, aus einem leeren Datenspeicher etwas raus zu holen, kein Fehler entsteht, sondern null ausgegeben wird.. Deswegen dürfen dann keine leeren Elemente gespeichert werden). Das mag den Verwender der Datentypen verleiten, schlampiger zu programmieren, statt vor Zugriffen z.B. mit istLeer den Speicher zu kontrollieren. Ärgerlicher ist aber, dass bei der Liste das aktuelle Element nicht automatisch gesetzt wird und dann das rein (bzw. insert) nicht funktioniert, ohne eine Meldung auszugeben oder einen Fehler zu erzeugen. Getäuscht durch den scheinbar problemlosen Ablauf werden Verwendungsfehler oft kaum oder zu spät erkannt, sodass die teilweise Fehlertoleranz nicht unbedingt zur Sicherheit programmierter Anwendungen beiträgt.
Andererseits wird durch die Vorgaben das didaktische Ziel, intensiv über die Datentypen nachzudenken und zu diskutieren, sowie verschiedene Implementationen zu probieren, zu vergleichen und zu bewerten, in besonderer Weise gefördert. Deshalb folgt auf einer Sonderseite die Implementation von Queue, Stack und List nach den aktuellen Vorgaben, zusammen mit einem Applet zum Ausprobieren und den vollständigen, kommentierten Quelltexten:
zum Seitenanfang / zum Seitenende
4. linearer abstrakter Datentyp: Sortierte Liste
Neben der normalen Liste interessieren oft auch geordnete Listen, in denen die Elemente in einer (einmal ausgewählten) festen Ordnung stehen. Damit man in einer solchen sortierten Liste nicht ordnungsschädigend herumpfuschen kann, wird sie hier nicht als vererbte Erweiterung einer normalen Liste implementiert (weil dann weiter und rein zur Verfügung stünden, und damit auch an falscher Stelle eingefügt werden kann). Vielmehr wird die normale Liste vor dem Anwender versteckt und der Zugriff nur noch über neue Methoden wie sortRein oder löscheGesucht ermöglicht.
Damit aber überhaupt eine Anordnung der Objekte möglich ist, muss eine Ordnungsrelation definiert werden. Dies geschieht hier mit der Methode vergleicheMit. Ein konkretes Beispiel für vergleicheMit befindet sich bereits am Ende meiner Java-Seite d).
| public interface E_ObjektMitOrdnung // Krell, 29.5.2004 -- www.r-krell.de { public double vergleicheMit (Object anderes, char sortKrit); // Hiermit wird -- ähnlich wie durch compareTo für Strings -- die Reihenfolge // zweier Objekte festgelegt. Anders als bei der vordef. Java-Methode bzw. Com- // parable kann noch ein Sortierkriterieum gewählt werden. Speichert man z.B. // Schüler mit Namen, Vornamen, Zeugnisnote und Alter, so soll mit dem zu über- // gebenden Buchstaben ausgesucht werden, welches Datenfeld der Sortierschlüssel // ist. Bei sortKrit='v' könnte z.B. alphabet. nach Vornamen sortiert werden, // während bei 'z' Schüler nach ihren Zeugnisnoten verglichen/geordnet werden. // Details müssen natürlich bei den konkreten Klassen formuliert werden, die // dieses Interface implementieren. // a.vergleicheMit(b, sortKrit) < 0 bedeutet a<b; ==0 <=> a=b; >0 <=> a>b // bezüglich des gewählten Sortierkriteriums. } |
Damit gelingt dann die Implementation einer sortierten Liste für Objekte, die das Interface E_ObjektMitOrdnung verwirklichen, etwa nach folgendem Muster:
| // Sortierte Liste -- Krell, 29.5.04 (www.r-krell.de) // Die sortierte Liste erwartet von den Elementen nur die im Interface E_ObjektMitOrdnung // festgelegte Methode. Andere Eigenschaften oder Fähigkeiten werden nicht verlangt. // Insofern ist diese Liste fast so allgemein wie die einfache Liste für beliebige // Objekte, nur dass statt Object jetzt E_ObjektMitOrdnung als Elementtyp verlangt wird. // Die tatsächliche Speicherung der Elemente geschieht in einer normalen einfachen Liste, // wobei die richtigen Stellen mit den dort vorhandenen Methoden wie anDenAnfang, weiter,.. // usw. gesucht bzw. gefunden werden. public class E_SortListe { E_Liste normaleListe; char sortKrit; public E_SortListe (char sortierKriterium) // Konstruktor: { // erzeugt normale Liste als Speicher normaleListe = new E_Liste(); // und legt einmalig das Sortierkriterium fest sortKrit = sortierKriterium; } public void sortRein (E_ObjektMitOrdnung neuerInhalt) //neues Element an der richtigen Stelle { // einfügen. "richtig" = entsprechend dem beim normaleListe.anDenAnfang(); // Erzeugen der Liste angegeben Kriterium while(!normaleListe.istAmEnde() && ((E_ObjektMitOrdnung)normaleListe.zeige()).vergleicheMit(neuerInhalt, sortKrit)<0) { normaleListe.weiter(); } normaleListe.rein(neuerInhalt); } public E_ObjektMitOrdnung zeigeGesucht (E_ObjektMitOrdnung gesucht) { //(erstes) Element finden und zurückgeben, das normaleListe.anDenAnfang(); // mit gesucht bezüglich des Sortierkriteriums while(!normaleListe.istAmEnde() // übereinstimmt && ((E_ObjektMitOrdnung)normaleListe.zeige()).vergleicheMit(gesucht, sortKrit)<0) { normaleListe.weiter(); } if (!normaleListe.istAmEnde() && ((E_ObjektMitOrdnung)normaleListe.zeige()).vergleicheMit(gesucht, sortKrit)==0) { return ((E_ObjektMitOrdnung)normaleListe.zeige()); } else { return (null); // gesuchtes Element nicht gefunden } } public E_ObjektMitOrdnung löscheGesucht (E_ObjektMitOrdnung gesucht) { //(erstes) Element zurückgeben und löschen, das normaleListe.anDenAnfang(); // mit gesucht bzgl. des Sortierkriteriums while(!normaleListe.istAmEnde() // übereinstimmt && ((E_ObjektMitOrdnung)normaleListe.zeige()).vergleicheMit(gesucht, sortKrit)<0) { normaleListe.weiter(); } if (!normaleListe.istAmEnde() && ((E_ObjektMitOrdnung)normaleListe.zeige()).vergleicheMit(gesucht, sortKrit)==0) { return ((E_ObjektMitOrdnung)normaleListe.raus()); } else { return (null); // gesuchtes Element war gar nicht vorhanden } } } |
Der Umgang mit der vorstehend beschriebenen alten, noch nicht parametrisierten sortierten Liste kann auf einer Sonderseite probiert werden:
Interaktiver Test der (alten) sortierten Liste (mit Java-Applet)
Auch bei der typsicheren parametrisierten sortierten Liste müssen die Elemente über eine Vergleichsmethode verfügen. Ein (parametrisiertes) Interface verspricht, dass Elemente vom ElTyp über die Methode vergleicheMit verfügen (s.o.):
| // Parametrisiertes Interface für die Verwendung mit der parametrisierten sortierten Liste // R. Krell, 21.4.2015 -- www.r-krell.de public interface P_MitOrdnung<ElTyp> // das Interface ist parametrisiert, weil.. { // .. der ElTyp nachfolgend in vergleicheMit gebraucht wird! public double vergleicheMit (ElTyp anderes, char sortKrit); // s. Kommentar in E_ObjektMitOrdnung } |
Damit gelingt die Implementation der typisierten sortierten Liste wie folgt:
| // Parametrisierte Sortierte Liste -- für IF Q1 M - R. Krell, 21.04.2015 (www.r-krell.de) public class P_SortListe <ElmOTyp extends P_MitOrdnung<ElmOTyp>> // Die Elemente -- hier vom Typ ElmOTyp = Element-mit-Ordnung -- müssen das Interface // P_MitOrdnung verwirklichen, d.h. tatsächlich über vergleicheMit verfügen. // In der Parameter-Angabe in <..> steht immer nur extends statt implements; // Bei der Ableitung eines Parameters von mehreren Interfaces und/oder (abstr.) Klassen // wird & verwendet, z.B. <ElmO extends P_MitOrdnung & P_MitZeige, ZweiterParameter>; // Inzwischen ist am Ende der Kopfzeile durchaus >> statt früher nur > > möglich. { Ls_Liste<ElmOTyp> normaleListe; char sortKrit; public P_SortListe (char sortierKriterium) // Konstruktor: { normaleListe = new Ls_Liste<ElmOTyp>(); // erzeugt normale Liste als Speicher sortKrit = sortierKriterium; // und legt einmalig das sortKrit fest } public void sortRein (ElmOTyp neuerInhalt) // neues Element an richtiger Stelle einfügen; { // "richtig" = für aufsteigende Reihenfolge normaleListe.anDenAnfang(); // bzgl. des Sortierkriteriums sortKrit while (!normaleListe.istHintermLetzten() && (normaleListe.zeige1().vergleicheMit(neuerInhalt, sortKrit) < 0)) { // ^vergleicheMit -- hier wird das Interface P_MitOrdnung für ElmOTyp ausgenutzt normaleListe.weiter(); } // end of while normaleListe.rein(neuerInhalt); } public ElmOTyp zeigeGesucht (ElmOTyp gesucht) { // (erstes) Element finden und zurückgeben, das normaleListe.anDenAnfang(); // mit gesucht bezüglich des Sortierkriteriums while(!normaleListe.istHintermLetzten() // übereinstimmt && (normaleListe.zeige1()).vergleicheMit(gesucht, sortKrit)<0) { normaleListe.weiter(); } if (!normaleListe.istHintermLetzten() && (normaleListe.zeige1()).vergleicheMit(gesucht, sortKrit)==0) { return (normaleListe.zeige1()); } else { return (null); } } public ElmOTyp löscheGesucht (ElmOTyp gesucht) { //(erstes) Element zurückgeben und löschen, das normaleListe.anDenAnfang(); // mit gesucht bezüglich des Sortierkriteriums while(!normaleListe.istHintermLetzten() // übereinstimmt && (normaleListe.zeige1()).vergleicheMit(gesucht, sortKrit)<0) { normaleListe.weiter(); } if (!normaleListe.istHintermLetzten() && (normaleListe.zeige1()).vergleicheMit(gesucht, sortKrit)==0) { return (normaleListe.raus()); } else { return (null); } } } |
Ein neues Applet erlaubt auch den Test der neuen generischen sortierten Liste:
Interaktiver Test der (neuen) sortierten Liste (mit Java-Applet und Quelltext)
Betrachtet man oben (in beiden Formen) die Methode zeigeGesucht, so ist ihr Aufwand leider linear von der Anzahl der Elemente in der Liste abhängig. Bei der Suche in sortierten Reihungen war hingegen mit dem Halbierungsverfahren (=binäre Suche) ein Algorithmus verwendet worden, der viel rascher, nämlich schon nach ~ log2(Elementzahl) Schritten zum Ziel fand. Über eine Verbesserung der Suche sollte also dringend nachgedacht werden -- eine Möglichkeit zeigt meine nächste Seite, „Informatik mit Java", Teil f). Dann muss allerdings eine andere Verknüpfung der Knoten her: In einer linearen Liste lässt sich keine bessere Suche bewerkstelligen, sodass die Sortierung bzw. überhaupt eine sortierte Liste nicht wirklich nützt.
zurück zur Informatik-Hauptseite
(Die anderen Java-Seiten werden entweder mit dem Menü hier am Seitenanfang oder
am besten auch auf der Informatik-Hauptseite ausgewählt)