Die Überschriften a) und b) verweisen auf die vorhergehenden Seiten, d) bis h)
auf nachfolgende Seiten| www.r-krell.de |
| Webangebot für Schule und Unterricht, Software, Fotovoltaik und mehr |
Willkommen/Übersicht > Informatik > Informatik-Seite c)
Teil c) Sortieren und Suchen
mit Swing-Oberfläche
Die Überschriften a) und b) verweisen auf die vorhergehenden Seiten, d) bis h)
auf nachfolgende Seiten
a) Grundlegendes zu Java, benötigte Software (inkl. Downloadadressen) und Installation
b) Programmieren mit Java - erste Programme, Kontrollstrukturen, Autorennen, Aufzug, Objekte
sowie Verweise auf fremde Java-Seiten
Diese Seite: "Informatik mit java", Teil c) --Swing-Oberfläche sowie Sortieren und Suchen in Java
d) Adressbuch- bzw. Fuhrpark-Verwaltung mit Java; Dateioperationen
e) Lineare Abstrakte Datentypen (Keller, Schlangen, Listen) und einige Anwendungen (z.B. Tiefen- und Breitensuche im
Labyrinth)
f) Abstrakter Datentyp Baum ([binärer] Sortierbaum, Rechenbaum, Spielbaum)
g) Abstrakter Datentyp Graph (Adjazenzmatrix u. -listen, typische Fragestellungen, Tiefen- u. Breitensuche)
h) Bau eines Compilers Java -> 1_AMOR (Syntaxdiagramm, Scanner, Parser, Variablentabelle,
Codeerzeuger)
...
Eine vollständige Übersicht aller "Informatik mit Java"-Seiten gibt's auf der Informatik-Hauptseite!
zum Seitenanfang / zum Seitenende
Einordnung und Vorüberlegung
Nachdem auf den vorangegangenen Seiten mit dem Java-Hamster bzw. mit Stift&Co programmiert wurde, sollen jetzt "richtige" Java-Programme ohne künstliche/zusätzliche Lernumgebungen in Angriff genommen werden. Algorithmisch werden dabei die einfachen Sortierverfahren sowie -- hier als einziges höheres Verfahren -- Quicksort erarbeitet und programmiert. Die Sortierverfahren arbeiten auf einer Reihung (array), sodass hierfür eine geeignete Klasse geschaffen werden muss. Was in der Reihung steht -- einfache Datentypen, Texte oder komplexe Objekte -- ist für den Sortier-Algorithmus letztlich egal. Statt wie im Folgenden Kommazahlen zu sortieren, wäre es natürlich viel motivierender, zunächst etwa mit einem Adressbuchprogramm zu beginnen, in dem die eigenen Freunde verwaltet werden. Dabei ergibt sich dann automatisch das Bedürfnis, das Adressbuch auf der Festplatte sichern zu können (damit nicht bei jedem Programmstart alle Freunde erneut eingegeben werden müssen). Außerdem wird schnell der Wunsch laut, die Freunde wahlweise nach Nachname, Vorname oder auch nach anderen Kriterien sortieren zu lassen, um gezielter auf eine bestimmte Personen zugreifen zu können, sodass dann Sortierverfahren motiviert erarbeitet und zum Projekt hinzugefügt werden können. Und natürlich hat das Adressbuch-Projekt eine moderne Oberfläche. Im Unterricht habe ich in den letzten Jahren tatsächlich zunehmend diesen Weg beschritten, und bin erst danach zur Festigung und Übung -- aber auch als Vorbereitung auf die bisherigen Anforderungen des Zentralabiturs, die zum Glück demnächst wohl etwas erweitert werden -- nochmal zum beispielhaften Sortieren von Zahlen zurück gekehrt.
Meine "Ausführlichen Seiten zur Informatik mit Java" habe ich allerdings schon früher begonnen. Auch wenn seither viele Seiten ergänzt und mehrfach aktualisiert bzw. überarbeitet wurden und ich Ende 2012 den Inhalt dieser Seite c) völlig neu gestaltet habe, wollte ich doch die alte Anordnung der Seiten nicht durchbrechen. So finden Sie ein Beispiel für eine Objektverwaltung -- statt befreundeter Personen sind es dort Autos -- erst auf der kommenden Seite d). Und hier werden eben dann doch zunächst nur Zahlen sortiert und erst im Anschluss ein Ausblick auf das Sortieren beliebiger Objekte nach verschiedenen Kriterien gegeben.
Allerdings soll auch ein Sortier-Programm für Zahlen 'ordentlich' aussehen und muss sich zeitgemäß bedienen lassen, braucht also eine grafische Oberfläche, die hier mit dem GUI-Builder vom Java-Editor (vgl. meine Seite a)) und jetzt mit der Swing-Bibliothek erstellt werden wird.
zum Seitenanfang / zum Seitenende
Entwurf einer Swing-Oberfläche
und Hinweise auf alte AWT-Oberflächen-Vorlagen und Beispiel-Applets
Früher habe ich Oberflächen mit der Java-AWT erstellt. Ein einfaches älteres Demo-Programm findet sich noch auf meiner Sonderseite "GUI-Oberfläche mit der Java-AWT, Währungsrechner und Geldrückgabeautomat", wo ein im Unterricht, zu Hause und bei Klassenarbeiten verwendetes Übungsblatt herunter geladen kann, damit man angelehnt an das aufgeführte Beispiel von Hand und auf Papier den Programmtext für eine entsprechende Oberfläche entwerfen konnte. Außerdem geht es dort zu einem Währungskurs-Umrechner-Applet und dem Applet eines Automaten, der Wechselgeld zurück gibt -- jeweils mit Quelltext. Beide Beispiele könnten natürlich genauso gut mit Swing geschrieben werden.
Jedenfalls soll die Oberfläche unseres Sortierprogramms mit der 'schöneren' Swing-Bibliothek erstellt werden. Benutzt wird der intuitive GUI-Builder des empfehlenswerten Java-Editors, einem kompakten Programm, das sich ideal für den Unterricht eignet (vgl. meine Seite a)). Im Allgemeinen reicht es, wenn die Schülerinnen und Schüler damit ansprechende und passende Oberflächen erzeugen und diese 'mit Leben' füllen können -- nur wenige wollen den automatisch erzeugten Java-Quelltext wirklich genau verstehen oder könnten ihn gar von Hand notieren (was sicher auch nicht nötig ist). Trotzdem hilft ein Blick in den automatisch erzeugten Text, um in eigenen Projekten eventuell weitere, nicht vom GUI-Builder bereitgestellte Grafik-Elemente oder Listener in analoger Weise von Hand zu ergänzen.
Weil verschiedene Sortier- und Suchverfahren programmiert und verglichen werden sollen, sind in der zu erstellenden Oberfläche schon Knöpfe (Schaltflächen) für mehrere Verfahren vorgesehen bzw. werden im Laufe der Projekt-Entwicklung hinzugefügt. Anfangs reicht eine Schaltfläche, um direkt den ersten programmierten Sortieralgorithmus ausprobieren zu können. Das Endprodukt (hier noch mit einem mit "..." beschrifteten, aber letztlich doch nicht genutzten Knopf) könnte etwa so aussehen:
Automatisch erzeugt der Javaeditor (hier in der Version 11.27 vom 5.12.2012) den zugehörigen Java-Quelltext, in den schließlich nur noch ein Objekt sortdemo der (ganz selbst zu schreibenden) Klasse Sort_2012 eingebunden werden muss, das die eigentliche Arbeit macht (also die Reihung, deren zufälliges Erzeugen und die Sortierverfahren enthält -- s.u.). Diese weitere Klasse sollte getrennt und unabhängig von der Oberfläche geschrieben werden und auch ohne bzw. mit ganz anderen Oberflächen funktionieren! Und an den automatisch mit //TO DO bezeichneten Stellen der Rahmenmethoden zu den Schaltflächen werden die gewünschten Aktionen eingebaut: Befehle im Zusammenhang mit der Oberfläche unmittelbar; zufälliges Erzeugen und Sortieren u.ä. durch Aufruf geeigneter Methoden aus dem Extraobjekt sortdemo (siehe rote Ergänzungen in den vorstehenden Bildern. Die Bilder können übrigens durch Anklicken größer in einem eigenen Fenster geöffnet oder durch Rechtsklick und "Bild speichern unter.." herunter geladen werden)
Während bei vielen anderen Projekten -- u.a. bei der Objektverwaltung -- oft die Oberfläche bestimmt, welche Methoden in der Extraklasse benötigt werden ("outside-in"-Entwurf), ist es hier wohl doch eher so, dass die unten programmierten Erzeugungs-, Sortier- und Suchverfahren jeweils eine eigene Schaltfläche benötigen und so das Aussehen der Oberfläche (mit-)bestimmen ("inside-out").
Der vollständige Quelltext der Oberfläche Sort_2012_Oberflaeche und der Startdatei befindet sich auf der Extraseite mit dem hier abgebildeten Applet (s.u.). Der Java-Programmtext der Extraklasse Sort_2012 mit den Verfahren wird weiter unten auf dieser Seite vorgestellt.
zum Seitenanfang / zum Seitenende
Der Datentyp und die Methoden für die eigentliche Arbeit
Im Unterricht sollten zuvor schon Reihungen (arrays) als strukturierte Variable behandelt worden sein, die eine vorher festgelegte Anzahl von Werten gleichen Typs aufnehmen können und den Zugriff auf jeden beliebigen Einzelwert (jede Komponente bzw. jedes Feld) per Index ermöglichen. In Java können nur nicht-negative ganze Zahlen als Index verwendet werden; die Nummerierung beginnt immer mit 0. Zwar gibt es in Java inzwischen auch viele dynamische Datentypen (etwa eine ArrayList), die auch noch zur Laufzeit vergrößert werden können, wenn plötzlich doch mehr Werte Platz finden sollen, als ursprünglich geplant. Für das Verständnis, wegen der historischen Bedeutung und weil noch überall davon zu lesen ist. wird hier aber eine normale, einfache und statische Reihung verwendet. Weil bis zu 200 Zahlen gewählt werden können, muss von Anfang an Platz für 200 Kommazahlen sein. Wird eine kleinere Anzahl gewählt, wird die Reihung eben nicht ganz gefüllt, sondern nur der vordere Teil wird lückenlos mit anzahl vielen Kommazahlen belegt. Damit später beim Sortieren nicht unnötigerweise nicht- bzw. zufällig gefüllte Bereiche mitsortiert oder ausgegeben werden, gehört der Wert anzahl als wichtiges Attribut zur Reihung und wird gemeinsam in der selben Klasse untergebracht. Im Übrigen wurde hier als Inhaltstyp der Typ double bzw. Kommazahl gewählt, damit man auch sofort am Typ den Inhalt (double) und den Index (int) unterscheiden kann bzw. der Compiler bei einer versehentlichen Vermischung eine Fehlermeldung auswirft.
Da das Erzeugen oder Sortieren Operationen auf dieser Reihung sind, werden sie als Methoden in der gleichen Klasse Sort_2012 notiert und arbeiten auf der dort definierten Reihung double [] reihe = new double [200]; und mit der int anzahl = 0; die den Startwert 0 erhält (der natürlich später, beim Erzeugen von Zufallszahlen, auf den dann gewählten Wert erhöht wird).
Die im Folgenden behandelten Sortierverfahren sind so genannte interne Sortierverfahren, die außer vielleicht einer Hilfsvariablen für einen einzigen herausgenommenen Wert keinen weiteren Speicherplatz benötigen, weil sie direkt die Reihung verändern. Will man hingegen mehrere verschiedene Verfahren auf genau die gleichen Zufallszahlen anwenden, um so den Aufwand besser vergleichen zu können, muss man die Reihung doch kopieren (Methode sichern): das Original reihe kann dann durch Sortieren verändert und ausgegeben werden, auf Wunsch (wiederherstellen) aber später auch wieder mit den Zahlen aus der zweiten Reihung backup überschrieben werden (um so die frühere, unsortierte Reihenfolge erneut herzustellen). Da Java bei Objekten mit der Zuweisung backup = reihe; der Reihung backup nur die Speicheradresse von reihe zuweisen würde (sodass beide Namen ab sofort synonym sind und nur für ein einziges, das selbe Objekt stehen), findet damit kein Kopieren oder Überschreiben alle Werte statt; dies geschieht hingegen mit der Methode clone(), die unten verwendet wird.
zum Seitenanfang / zum Seitenende
Viele der einfachen Sortierverfahren entdecken Schülerinnen und Schüler erfahrungsgemäß selbst, wenn sie beispielsweise in einer Doppelstunde in kleinen Gruppen echte Gegenstände wie Spielkarten, Bücher oder CDs von Hand sortieren und das verwendete Verfahren für ihre Mitschüler nachvollziehbar beschreiben und später formalisieren bzw. programmieren sollen. Gerade das Sortieren von CDs bzw. CD-Hüllen in einem unterteilten CD-Regal oder -Rack zeigt sofort die Analogie zur Reihung. Fehlt wirklich zunächst ein Verfahren, kann nach der Programmierung und dem Test der ersten Verfahren leicht ein weiteres Verfahren nach wenigen Anregungen entwickelt werden. Nur Quicksort ist erkennbar schwerer -- nicht nur wegen der ungewohnten rekursiven Beschreibung, sondern auch wegen der "Teile- und Herrsche"-Strategie und der zunächst gewöhnungsbedürftigen Aufteilung in die Elemente, die kleiner (oder gleich) dem zufällig gewählten Pivot-Element sind, und die anderen. Simulationsprogramme, die den Sortiervorgang visuell deutlich machen, sind dabei hilfreich
Weil viele Lehrbücher und Webseiten didaktische Hinführungen zu den Sortierverfahren bieten (u.a. http://www.matheprisma.uni-wuppertal.de/Module/Sortieren/index.htm), soll hier auf weitere Erläuterungen verzichtet werden und es wird die fertige Java-Programmierung vorgestellt. Schülerinnen und Schüler sollte allerdings genügend Zeit zur Entwicklung der Methoden gelassen werden -- nur durch eigenen Probieren und eigene Fehler lernt man die Technik des Programmierens selbst!
Zu den Suchmethoden folgt noch eine anschauliche Erläuterung nach dem Programmtext im Abschnitt "Nachtrag/Ergänzung zum Suchen" weiter unten. Und danach folt die beispielhafte Untersuchung des Aufwands eines Sortierverfahrens mit Tabellen zum asymptotischen Verhalten und der Definition von 'natürlich' und 'stabil' im Kapitel "Aufwands-Analyse von Sortier-Verfahren".
zum Seitenanfang / zum Seitenende
Reihung und Hilfsmethoden
Zunächst werden, wie oben erläutert, die Reihung(en) mit dem wichtigen anzahl-Attribut sowie die Methode zum Füllen mit Zufallszahlen einige weitere Hilfsmethoden angegeben:
| public class Sort_2012 // = Sortieren (und Suchen) von Kommazahlen // R. Krell, 14.9.2012/14.12.12012 für IF EF-M bzw. inzwischen Q1-M bzw. www.r-krell.de { double [] reihe = new double [200]; // Original, wird erzeugt, sortiert & ausgegeben double [] backup = new double [200]; // Backup zur späteren Wiederherstellung des Originals int anzahl = 0; // Füllgrad der Reihung(en) reihe (und backup) public void fülleZufällig (int wieviele) { // füllt die reihe von links mit der in wieviele for(int i=0; i<wieviele; i++) // angegeben Anzahl von zufälligen Kommazahlen { reihe[i] = zufallszahl(); // erzeugt Zufallszahlen zwischen 0.0 und 9.9, s.u. } anzahl=wieviele; // setzt anzahl auf den richtigen, neuen Wert } private double zufallszahl() { return (((int)(100*Math.random()))/10.0); // Zufallszahl zw. 0.0 und 9.9 } // mit einer Nachkommastelle public void sichern() { backup = reihe.clone(); // kopiert die Werte der Original-reihe in backup } public void wiederherstellen() { reihe = backup.clone(); // setzt reihe auf die Werte aus dem backup zurück } public String zeigeAlle() // übergibt den Inhalt der Reihe als lange Textzeile { // für die Anzeige in einer Oberfläche String ausgabe = "Reihe :"; // oder die Ausgabe mit System.out.println(..) for(int i= 0; i < anzahl;i++) { ausgabe= ausgabe+" "+reihe[i]; } return (ausgabe); } //-------------------- Hilfmethode für die folgenden Sortierverfahren -------- private void tausche (int i, int j) // tauscht die Inhalte(!), // die in der reihe an den Positionen i und j stehen/standen { double hilfe = reihe[i]; reihe[i] = reihe[j]; reihe[j] = hilfe; } |
zum Seitenanfang / zum Seitenende
Einfache Sortierverfahren (iterativ) - Teil 1
Jetzt folgt der erste Teil, in dem die Sortiermethoden stehen. Viele benutzen die oben angegebene Methode tausche!
| //-------------------- Einfache Sortierverfahren, iterativ -------------------- public void bubbleSort() // Sortieren durch Vertauschung direkter Nachbarn { // Erste Version mit fester Durchgangszahl for (int durchg = 1; durchg < anzahl; durchg++) // mehrere Durchgänge.. { for(int i=0; i<anzahl-durchg; i++) //.. die kürzer werden, weil sich hinten { // die großen Zahlen Sammeln if (reihe[i] > reihe [i+1]) // bei Bedarf { tausche(i, i+1); // Vertauschen unmittelbarer Nachbarn } } } } public void bubbleSort2() // BubbleSort Version 2: bedarfsabhängige Durchgangszahl { boolean getauscht; // merkt sich, ob im letzten Durchgang getauscht wurde int durchg = 1; do { getauscht = false; // noch nicht getauscht for (int i = 0; i < anzahl-durchg; i++) // ein Durchgang { if (reihe [i] > reihe [i+1]) { tausche (i, i+1); // bei Bedarf Nachbarn tauschen getauscht = true; // und Tausch merken } } durchg ++; // Vorbereiten für evtl. nächsten Durchgang } while(getauscht); // weiterer Durchgang nur nötig, wenn im letzten } // Durchgang noch getauscht wurde public void maxSort() // Sortieren durch Auswahl -- hier des jeweils größten Elements { // = "SelectionSort"; (Quelltext nochmal verbessert am 23.2.2013) int maxStelle; for (int durchg = anzahl-1; durchg > 0; durchg --) { // rückwärts zählen, da große Zahlen nach hinten. // Bleibt nur noch 1 Element übrig (reihe[0]), ist dies automatisch das größte maxStelle = durchg; // Position des bisher größten Elements for (int i= durchg-1; i>=0; i--) // reihe[durchg] braucht nicht mit sich selbst verglichen werden,.. { // .. sonst aber mit allen Elementen davor if (reihe[i]> reihe[maxStelle]) // falls größeres Element gefunden.. { maxStelle = i; //.. Position aktualisieren } } tausche (maxStelle,durchg); // größtes Element nach hinten tauschen } } |
zum Seitenanfang / zum Seitenende
Einfache Sortierverfahren (iterativ) - Teil 2
Jetzt folgt der zweite Teil der einfachen Sortiermethoden (minSort funktioniert analog zum vorstehenden maxSort als Sortieren durch Auswahl/SelectionSort):
| public void minSort() // Sortieren durch Auswahl -- hier des jeweils kleinsten Elements { int minStelle; for (int durchg =0; durchg < anzahl-1; durchg++) { // aufsteigend, da kleine Elemente nach vorne kommen minStelle = durchg; for(int i=durchg+1; i<anzahl; i++) { if (reihe[i] < reihe[minStelle]) { minStelle = i; } } tausche (minStelle,durchg); // kleinstes Element nach vorne tauschen } } public void einSort() // Sortieren durch Einfügen, "InsertionSort" { double zwischenspeicher; // für vorderes Element aus unsortiertem Teil for (int durchg=1; durchg < anzahl; durchg++) { zwischenspeicher = reihe [durchg]; // herausnehmen int i = durchg-1; while (i >= 0 && reihe[i] > zwischenspeicher) { // größere sortierte Elemente schieben: reihe[i+1] = reihe[i]; // der wert von reihe[i] wird in die reihe[i+1] gesteckt i--; } reihe[i+1] = zwischenspeicher; // herausgenommenes Element nach vorne in erzeugte Lücke } } public void shakerSort () // ähnlich BubbleSort, nur Hin und Her { for (int durchg = 1; durchg <= anzahl/2; durchg++) { for (int i = anzahl-durchg-1; i>=durchg-1; i--) // Durchgang nach links { if (reihe[i] > reihe[i+1]) { tausche (i, i+1); } // fördert kleinstes Element nach links } for (int j = durchg; j < anzahl-durchg; j++) // Durchgang nach rechts { if (reihe[j] > reihe[j+1]) { tausche (j, j+1); } // fördert größtes Element nach rechts } } } public void weitere () { // ggf. weitere Verfahren, noch nicht implementiert. } |
zum Seitenanfang / zum Seitenende
Einfache Sortierverfahren (rekursiv)
Zu Übungszwecken, um sich schon vor Quicksort an die rekursive Darstellung zu gewöhnen, wurde die erste BubbleSort-Version auch in zwei verschiedenen rekursiven Varianten ausprobiert:
| //-------------------- Einfache Sortierverfahren, rekursiv ------------------- public void bubbleSortR() { bubble_rek (1); // ruft rekursives Bubblesort ab durchgang 1 auf } private void bubble_rek (int durchg) { // weniger rekursiv als folgende Variante "bubble_rekursiv" if (durchg < anzahl) { for(int i=0; i<anzahl-durchg; i++) // Schleife für einen Durchgang { if (reihe[i] > reihe [i+1]) { tausche(i, i+1); } } bubble_rek (durchg+1); // Rekursion nur für nächsten Durchgang } } public void bubbleSortR1() { bubble_rekursiv (0,1); // ruft rekursives Bubblesort ab Stelle i=0 im durchgang 1 auf } private void bubble_rekursiv (int i, int durchg) // massiv-rekursiv { if (i < anzahl-durchg) { if (reihe[i] > reihe [i+1]) { tausche(i, i+1); } // per Rekursion.. bubble_rekursiv (i+1, durchg); // im gleichen Durchgang zur nächsten Stelle/zum nächsten Paar } else // hinten im Durchgang angekommen { if (durchg < anzahl) // wenn noch ein Durchgang möglich ist { bubble_rekursiv (0, durchg+1); // vorne (bei Stelle 0) im nächsten Durchgang anfangen } } } |
zum Seitenanfang / zum Seitenende
![Quicksort mit ganzen Zahlen -- Zwischenzustand. Pivot=reihe[(li+re)/2], hier 39](if-c-quick.gif)
QuickSort
Als höheres Sortierverfahren ist hier Quicksort angegeben. Eine etwas andere Variante findet sich übrigens auf meiner Seite SWE "Objektorientierte Anwendungsentwicklung und Software-Engineering" in der Klasse AV_Filiale.
Dort wurden u.a. die beiden Abfragen am Ende, vor den rekursiven Aufrufen, einmalig an den Anfang der rekursiven Methode verlagert. Das spart zwar
etwas Programmierarbeit, schadet aber der Performance, weil jetzt insgesamt anzahl zusätzliche Rekursionen aufgerufen werden, um
sofort wieder als unnötig zu enden -- nämlich bei jedem auf ein oder kein Element geschrumpften Teilstück.
Die Bezeichnungen grün und rot beziehen sich auf eine Visualisierung des Verfahrens, die im Unterricht verwendet wurde.
| //-------------------- Höheres Sortierverfahren: QuickSort ------------------- public void quickSort () { quick_rek (0, anzahl-1); // startet rekursives QuickSort } private void quick_rek (int li, int re) // vgl. http://www.vogella.com/articles/JavaAlgorithmsQuicksort/article.html { int grün = li; // Index, läuft von links nach rechts int rot = re; // Index, läuft von rechts nach links double pivot = reihe[li]; // irgendein willkürlich gewählter.. // double pivot = reihe[re]; // .. Inhalt aus der reihe, irgendwo // double pivot = reihe[(li+re)/2]; // zwischen li und re. // double pivot = (reihe[li]+reihe[re])/2.0; // Künstliche Werte // double pivot = Math.sqrt(reihe[li]*reihe[re]); // gehen auch while (grün < rot) // offenbar auch <= möglich { while (reihe[grün] < pivot) // grün nach rechts bis zur Stelle des nächsten Tauschkandidaten { grün++; } while (reihe[rot] > pivot) // rot nach links bis zur Stelle des nächsten Tauschkandidaten { rot--; } if (grün <= rot) { tausche (grün, rot); // Inhalte der reihe von den beiden Stellen vertauschen; nicht grün und rot selbst grün++; rot--; // Vertauschte Inhalte sind keine Tauschkandidaten mehr } } // Schleife läuft, bis sich grün und rot überkreuzt haben if (li<rot) { quick_rek (li, rot); // Rekursion für linken Teil (alles <= pivot) } if (grün < re) { quick_rek (grün, re); // Rekursion für rechten Teil (alles >= pivot) } // meist stoßen die Teile direkt aneinander. Gelegentlich kann dazwischen // noch ein Element vom Wert des pivot-Elements stehen, das als // einzelnes Element nicht mehr sortiert werden muss! } |
zum Seitenanfang / zum Seitenende
Suchverfahren 1
Sortieren ist keine Selbstzweck, sondern soll effektives Suchen ermöglichen. Zunächst wird allerdings das primitive, vollständige
Durchsuchen der ganzen Reihung angegeben, das ohne und mit Sortierung gleichermaßen funktioniert. Dabei wird das erste passende Element
gefunden und seine Fundstelle innerhalb der Reihung, nämlich sein Index, zurück gegeben. Werden später nicht nur Zahlen, sondern
kompliziertere Objekte durchsucht -- zum Beispiel eine Reihung von Personen bis zum ersten Auftreten eines gesuchten Nachnamens -- kann über
diesen Index dann das ganze Objekt gelesen und weitere Eigenschaften wie Vorname, Geburtsdatum u.ä. ausgegeben werden. Die Zahl oder das
Element, das ganz vorne bzw, ganz links in der Reihung steht, hat bekanntlich den Index 0. Deshalb darf nicht 0, sondern muss z.B. der
unmögliche negative Index -1 zurück gegeben werden, wenn ein Element gesucht wurde, das gar nicht in der Reihung steht.
Bei einem vorhandenen Element sind zwischen 1 (Element steht ganz links auf Index 0) bis anzahl (Element steht am Ende des gefüllten
Teils auf dem Index anzahl-1) Schleifendurchläufe (=Vergleiche = Suchschritte) nötig. Oder es werden (anzahl+1)
Schritte benötigt, wenn die gesuchte Zahl nicht vorhanden ist. Wäre eine (ausreichend groß dimensionierte) reihe z.B.
sogar mit 100000 Kommazahlen gefüllt, so wären zwischen 1 und 100001 Suchschritte nötig -- im Mittel 50000; bei der Suche nach einem
nicht vorhandene Element aber alle 100001. Der Aufwand ist linear, nämlich von der Ordnung O(anzahl).
| //-------------------- Versch. Suchverfahren: ---------------------------- public int suche1 (double gesucht) // normale, sequentielle Suche. // braucht keine Sortierung und nutzt diese, falls vorhanden, auch nicht aus! { int i=0; while (i<anzahl && gesucht != reihe[i]) { i++; } if (i<anzahl) { return (i); // gefunden an Stelle i } else { return (-1); // nicht gefunden } } public int suche1r (double gesucht) // wie suche1, nur rekursiv { return (suche_rek (0, gesucht)); } private int suche_rek (int i, double gesucht) { if (i < anzahl) { if (gesucht == reihe[i]) { return (i); } else { return (suche_rek (i+1, gesucht)); } } else { return (-1); } } |
zum Seitenanfang / zum Seitenende
Suchverfahren 1a
Das vorstehende vollständige Suchverfahren wird leicht abgewandelt, in dem bei der Suche nach nicht vorhandenen Elementen die Sortierung von reihe ausgenutzt wird: Kommt man an eine Zahl, die größer ist als die gesuchte, kann die gesuchte Zahl nicht mehr in der aufsteigend sortiert vorausgesetzten Reihung stehen und -1 wird zurück gegeben. Damit ist die Suche nach einem nicht vorhandenen Element genau so schnell, wie die nach einem vorhandenen Element und erfordert im Mittel anzahl/2 Schritte. Der Aufwand bleibt O(anzahl).
| public int suche1s (double gesucht) // sequentielle Suche nur // für eine aufsteigend sortierte Reihung. Minimal schneller als suche1, // falls gesuchtes Element nicht in der Reihung. Lohnt nicht!! { int i=0; while (i<anzahl && gesucht < reihe[i]) { i++; } if (i<anzahl && gesucht == reihe[i]) { return (i); // gefunden an Stelle i } else { return (-1); // nicht gefunden } } |
zum Seitenanfang / zum Seitenende
Suchverfahren 2: binäre Suche (= Halbierungsverfahren = Bisektionsverfahren)
Erst jetzt wird wirklich die Sortierung genutzt und der Suchaufwand drastisch auf O(log2(anzahl)) verkleinert: In einer Reihung mit 100000 Elementen würden höchstens 17 Schritte gebraucht, um ein Element zu finden bzw. das Nichtvorhandensein des gesuchten Elements festzustellen. Das Verfahren wird sowohl iterativ wie rekursiv angegeben.
| public int suche2 (double gesucht) // binäre Suche = Suche nach dem // Halbierungsverfahren; nur für aufsteigend sortierte Reihung. // Viel schneller als suche1, vorallem bei großer Anzahl! { int links = 0; int rechts = anzahl-1; int mitte; do { mitte = (links+rechts)/2; if (gesucht < reihe[mitte]) { rechts = mitte-1; } else { if (gesucht > reihe[mitte]) { links = mitte+1; } else // da weder < noch > wird == gefunden! { return (mitte); // bei Erfolg wird die Methode beendet } } } while (links <= rechts); // do..while-Schleife endet hier nur, wenn nichts gefunden wurde: return(-1); } public int suche2r (double gesucht) { return (bin_rek (0, anzahl-1, gesucht)); // ruft rekursive binäre Suche auf } private int bin_rek (int links, int rechts, double gesucht) { if (links <= rechts) { int mitte = (links+rechts)/2; if (gesucht < reihe[mitte]) { return (bin_rek (links, mitte-1, gesucht)); } else { if (gesucht > reihe[mitte]) { return (bin_rek (mitte+1, rechts, gesucht)); } else // da weder < noch > wird == gefunden! { return (mitte); } } } else { return (-1); } } } // Ende der Klasse Sort_2012 |
Mit dem vorstehenden letzten Teil ist die Klasse Sort_2012 fertig: Alle durch die Knöpfe der Oberfläche erreich- bzw. aufrufbaren Methoden sind geschrieben und liegen im Quelltext vor!
zum Seitenanfang / zum Seitenende
Das vollständige Sortierprogramm als ausführbares Applet
Das vollständige, oben dargestellte Sortierprogramm kann auf der
Extra-Seite: Such- und Sortier-Demo von Kommazahlen (als Java-Applet)
ausprobiert werden. Dort findet sich auch der Quelltext der Oberfläche bzw. der gesamte Quelltext zum Download.
zum Seitenanfang / zum Seitenende
Nachtrag/Ergänzung zum Suchen
Sind die Daten oder Zahlen ungeordnet - man stelle sich nur ein zufällig zusammen gemischtes Telefonbuch vor, wo die Namen nicht dem Alphabet folgen - muss man im schlimmsten Fall das ganze Buch von Anfang bis Ende Namen für Namen durchlesen, um eine gesuchte Person zu finden. Bei 100000 Einträgen bedeutet das bis zu 100000 Lesezugriffe und Vergleiche mit dem gesuchten Namen. Natürlich kann man Glück haben und findet den Namen schon früh. Aber genauso wahrscheinlich ist das Pech, dass der Namen erst weit hinten steht. Im statistischen Mittel muss man mit 50000 Vergleichen rechnen, wenn der Name tatsächlich im Telefonbuch steht. Ob ein Name fehlt, kann man hingegen erst am Ende nach 100000 Vergleichen sicher wissen.
Gleiches gilt für Reihungen mit Kommzahlen, die hier die Rolle des Telefonbuchs übernehmen: In ungeordneten Reihen kann eine vorhandene Zahl nach durchschnittlich 0.5*anzahl Vergleichen gefunden werden; eine nicht vorhandene Zahl zwingt immer zum vollständigen Durchsuchen der Reihung mit anzahl Vergleichen -- s.o. Suchverfahren 1 bzw. suche1.
Geordnete Telefonbücher und Zahlenreihen
erleichtern hingegen die Suche (und deswegen treibt man den oben beschriebenen Sortieraufwand überhaupt): Selbst wenn man weiterhin von vorne
an jeden Namen liest, weiß man spätestens bei 'Mozilla', dass der gesuchte 'Mozart' keinen Eintrag mehr im Telefonbuch besitzt. Also
auch bei der Suche nach nicht vorhandenen Elementen braucht die durchschnittliche Suche nur noch 0.5*anzahl Vergleiche, was immerhin einer Reduzierung auf die Hälfte entspricht. Bei vorhandenen
Namen oder Zahlen hat man aber mit der einfachen sequentiellen (oder besser: sequenziellen) Suche keinen Vorteil, weshalb sie nicht wirklich lohnt
-- siehe oben Suchverfahren 2 bzw. suche2.
Wie wir alle wissen, kann man aber viel geschickter suchen: selbst wenn man das Telefonbuch aufs Gratewohl irgendwo auf schlägt, sieht man sofort, ob der gesuchte Name weiter vorne oder weiter hinten stehen muss. Wenn man jetzt zunehmend kleinere Seitenpäckchen umblättert, kommt man rasch zum gesuchten Namen - hier reichen log2 (anzahl) Vergleiche, d.h. im Telefonbuch mit 100000 Einträgen kommt man spätestens nach log2(100000) = 17 Vergleichen (aufgerundet) zum Ergebnis, für die Suche im doppelt so dicken Telefonbuch mit 200000 Einträgen braucht man nicht doppelt so lange, sondern nur 18 Schritte bzw. Vergleiche bis zum Auffinden des gesuchten Namens oder der Gewissheit, dass der gesuchte Name nicht vorhanden ist. Achtzehn Schritte statt zweihunderttausend - das ist eine ganz erhebliche Ersparnis (siehe Tabelle am Ende des nachfolgenden Kapitels)!
Ein viele Jahre altes Übungsblatt zum Thema kann durch Anklicken lesbarer vergrößert oder (besser) hier als pdf-Datei (14 kB) abgerufen werden.
Allerdings stellte sich damals im Unterricht rasch heraus, dass das dort in Aufgabe 2b) vorgeschlagene Vorgehen mit fortgesetztem Halbieren der
Sprungweite wegen der Kumulierung von Rundungsfehlern (Halbe werden immer wieder abgerundet) ungeschickt und letztlich fehlerhaft ist: Ein
Halbieren des jeweils tatsächlich übrig bleibenden Bereichs erwies sich als günstiger! Umfangreichere Untersuchungen und
Bleistifttest führten schließlich zu einem brauchbaren Algorithmus, wie er längst oben in der Klasse Sort_2012 als
Suchverfahren 2 bzw. suche2 implementiert ist.
zum Seitenanfang / zum Seitenende
Aufwands-Analyse von Sortier-Verfahren
inkl. Zählern für Vergleiche und für Umspeicherungen, theoretischer
Analyse,
Natürlichkeit/Stabilität und Vergleichstabelle für den Aufwand
Die einfachen Sortierverfahren haben einen durch O(anzahl2) abgeschätzten Aufwand, während QuickSort im besten und im mittleren Fall O(anzahl*log2(anzahl)) schafft und nur im (seltenen) schlechtesten Fall den Aufwand der einfachen Verfahren hat. Um dieses Grenzverhalten zu begründen und trotzdem Unterschiede deutlich zu machen, wird üblicherweise gezählt bzw. berechnet,
Oft wird dabei der günstigste (best case) vom schlechtesten Fall (worst case) unterschieden bzw. noch das mittlere, also durchschnittliche Laufzeitverhalten angegeben (average case).
Wie oft Vergleiche zwischen Indizes (z.B. in QuickSort bei while (grün < rot).. ) oder Veränderungen an den Indizes (z.B. durch i++) vorgenommen werden, interessiert im Allgemeinen nicht. Dies liegt wohl daran, dass in anderen/alten Programmiersprachen (etwa auch in Pascal bzw. Delphi) die Inhalte der Reihungselemente tatsächlich in der Reihung standen. Wurden statt Zahlen komplexere Objekte sortiert, die viel Speicherplatz verbrauchten, war eine Umspeicherung oft mit erheblichem Kopieraufwand verbunden und fiel zeitlich ins Gewicht. Auch bei einer unnötig groß dimensionerten Reihung wurde viel Speicherplatz verschenkt. In Java stehen hingegen nicht die Inhalte der Objekte in der reihe, sondern nur die Speicherstelle (Adresse), wo der Anfang des Objektes im Hauptspeicher zu finden ist. Diese Adressen sind Zahlen, egal wie groß das Objekt ist (auch bei einem großen Mehrfamilienhaus ist die Hausnummer nicht größer als bei einem kleinen Einfamilenhaus). Insofern braucht in Java eine Umspeicherung von einem großen Objekt nicht mehr Zeit als bei einem kleinen (weil praktisch nur die Hausnummer-Schilder hin und her bewegt werden). Und der Zugriff ist trotz eventuell doppelt so langer Adresszahlen im Gegensatz zu den als Indizes verwendeten normalen Ganzzahlen unwesentlich langsamer als der Zugriff auf eine Indexzahl. Trotzdem bleibt es in Lehrbüchern, Lehrplänen und im Zentralabitur bei der historisch bedingten, auf Feldelemente eingeschränkten Betrachtungsweise, der ich deshalb auch hier folge.
In Java sind bei komplexen Elementen übrigens eher die Vergleiche von oder mit Reihungselementen zeitaufwändig, insbesondere wenn erst passende Attribute herausgesucht und mit Methoden wie compareTo bzw. vergleicheMit verglichen werden müssen (s.u.). Da ist der Vergleich von Indexzahlen mit einem Operator wie "<", "<=" oder ">" sicher schneller und kann vielleicht doch vernachlässigt werden.
Es genügt übrigens die Betrachtung des Rechen- bzw. Zeitaufwands -- eine Betrachtung des benötigten Speicherplatzes entfällt, da alle hier vorgestellten Verfahren intern sortieren und außer der reihe nur noch Platz für ein einziges weiteres Element benötigen, sodass beim Speicherbedarf keine wirklichen Unterschiede auftreten (obwohl das rekursiv programmierte Quicksort für die Verwaltung mehrerer gleichzeitig geöffneter Rekursionsstufen doch etwas zusätzlichen Speicherplatz braucht, was aber ebenfalls vernachlässigt werden soll).
Am Beispiel eines Sortierverfahrens gezeigt werden, wo bzw. wie durch Einbau geeigneter Zähler der Aufwand im oben beschriebene Sinne
verdeutlicht werden kann. Gewählt wurde minSort als erstes Verfahren aus Teil 2 der einfachen Sortierverfahren (s.o.), die
Ergänzungen sind farbig hervorgehoben und unterstrichen:
| public void minSort() // Sortieren durch Auswahl -- hier des jeweils kleinsten Elements { int zVergleichen = 0; // Zähler für die Vergleiche mit Kompenenten von reihe int zUmspeichern = 0; // Zähler für die Umspeicherungen von Kompenenten der reihe int minStelle; for (int durchg =0; durchg < anzahl-1; durchg++) { // aufsteigend, da kleine Elemente nach vorne kommen minStelle = durchg; for(int i=durchg+1; i<anzahl; i++) { zVergleichen ++; // Zähler vor dem nachfolgenden if einbauen, das sonst nur bei < gezählt wird if (reihe[i] < reihe[minStelle]) { minStelle = i; } } tausche (minStelle,durchg); // kleinstes Element nach vorne tauschen zUmspeichern = zUmspeichern + 3; // Ein Tauschen erfordert drei Umspeicherungen, vgl. 3 Zeilen in tausche } System.out.println ("minSort Aufwand: "+zVergleichen+" Vergleiche und " +zUmspeichern+" Umspeicherungen."); } |
Im Unterricht und in Klausuren werden natürlich auch theoretische Betrachtungen bzw. Berechnungen des Aufwands verlangt, die hier für
minSort nur ganz kurz angedeutet seien:
Werden anzahl = n Element mit obigem Verfahren sortiert, dann gibt es n-1 Durchgänge der äußeren for-Schleife
(von durchg=0 bis durchg=n-2). Bei durchg=0 läuft die innere for-Schleife n-1 mal ab (nämlich von
i=1 bis i=n-1). Da bei jedem Durchlauf der inneren Schleife genau einmal (jeweils mit der if-Abfrage) Reihungselemente
verglichen werden, finden für durchg=0 also n-1 Vergleiche statt. Wird in der äußeren Schleife dann durchg=1
gesetzt, läuft die innere Schleife noch von i=2 bis i=n-1, also n-2 mal ab, und es kommt entsprechend zu n-2 Vergleichen. Für
durchg=2 gibt es entsprechend n-3 innere Schleifenabläufe und damit n-3 Vergleiche, usw. Beim letzten äußeren
Schleifendurchgang (durchg=n-2) findet innen noch ein Durchlauf und damit ein letzter Vergleich statt. Das ergibt für die
Zahl der Vergleiche n-1 + n-2 + n-3 + ... + 3 + 2 + 1 mit insgesamt n-1 Summanden. Nach der Idee vom kleinen C. F.
Gauß werden der erste und letzte Summand n-1 + 1 = n, der zweite und vorletzte Summand n-2 + 2 = n usw. addiert, d.h. es gibt (n-1)/2 Paare
jeweils mit der Summe n, sodass ingesamt (n-1)/2 * n = (n2 - n)/2 = 1/2 n2 - 1/2
n die Anzahl der Vergleiche ist (wobei hier der Bruchstrich '/' mathematisch gemeint ist und nicht die Java-Ganzzahl-Division bedeutet).
Da hingegen nie in der inneren, sondern immer nur am Ende der äußeren Schleife bei jedem Durchgang genau einmal getauscht wird, wird
tausche insgesamt n-1 mal aufgerufen. Jedes Tauschen über die Hilfsvariable bedeutet 3 Umspeicherungen von Reihungselementen, so dass
die Gesamtzahl der Umspeicherungen durch 3*(n-1) = 3n - 3 beschrieben wird.
Besonders interessiert man sich für den Aufwand bei sehr großen n, also für den asymptotischen Fall. Wie bei der Kurvendiskussion bzw. Funktionsuntersuchung ganzrationaler Funktionen im Mathematikunterricht das asymptotische Verhalten allein am Summand mit der höchsten Potenz von x abgelesen werden kann, und vom Vorfaktor/Koeffizient nur das Vorzeichen interessiert (was beim Sortieren immer positiv ist), wird das Aufwands-Verhalten für wachsendes n durch die jeweils höchste Potenz von n im gefunden Aufwands-Term charakterisiert, d.h. bei minSort ist der Vergleichsaufwand von der Ordnung O(n2) und der Umspeicheraufwand von O(n), wobei der Gesamtaufwand natürlich wieder von der höheren Potenz majorisiert wird und daher insgesamt O(n2) ist. Das große O bei z.B. O(n2), das die asymptotische (Aufwands-)Ordnung angibt, wird übrigens Landau-Symbol genannt.
Ungewöhnlicherweise hängt der Aufwand bei diesem Verfahren überhaupt nicht vom Inhalt der reihe ab, d.h. der Aufwand für das Sortieren mit minSort ist immer gleich, egal ob die Reihung bereits richtig aufsteigend sortiert war, ob sie zuvor absteigend oder noch überhaupt nicht sortiert war -- d.h. der Aufwand ist hier für alle Fälle (best, average und worst case) gleich! Damit kann minSort gerade noch als natürlich bezeichnet werden: Bekanntlich heißt ein Sortieralgorithmus genau dann "natürlich", wenn sein Aufwand am kleinsten ist, wenn eine bereits richtig sortierte Reihung nochmal sortiert wird -- zumindest darf der Aufwand dann nicht größer sein als bei irgend einer anderen Vorsortierung.
Neben der "Natürlichkeit" wird übrigens oft noch die -- vom Aufwand allerdings völlig unabhängige -- "Stabilität" zur
Klassifizierung von Sortierverfahren herangezogen: Ein Sortieralgorithmus heißt genau dann "stabil", wenn Elemente mit
gleichem (Schlüssel-)Wert ihre Reihenfolge beibehalten. Das ist bei minSort nicht der Fall: Betrachtet man etwa die Reihung aus den
vier Kommazahlen 8.01, 8.02, 3.5 und 9.7, dann wird beim Nachvollziehen / Bleistifttest des Verfahrens ersichtlich, dass im
ersten Durchgang der äußeren for-Schleife als kleinste Zahl 3.5 an der minStelle = 2 gefunden und nach vorne getauscht
wird, wodurch die vordere 8.0 (=8.01) nach hinten wandert. Es ergibt sich dadurch die neue Reihenfolge 3.5, 8.02,
8.01, 9.7, die bis zum Ende beibehalten wird.
Werden nur Kommazahlen sortiert, lassen sich gleiche Zahlen nicht unterscheiden und die Stabilität oder Nichtstabilität spielt keine
Rolle. Anders ist es hingegen, wenn größere Objekte (Strings nach einzelnen Buchstaben, komplexere Objekte nach nur einem
bestimmten Attribut je nach Sortierkriterium -- s.u.) nur nach einem Teil ihres Inhalts sortiert werden. Dann könnte es wichtig sein, dass
eine Vorsortierung erhalten bleibt -- weswegen minSort in solchen Fällen dann nicht eingesetzt werden darf.
Für die Analyse der anderen Sortierverfahren muss auf die Literatur oder z.B. auch auf die oben (im Abschnitt "Methoden: Sortierverfahren entdecken") schon genannten Mathe-Prisma-Webseite verwiesen werden.
| anzahl der Elemente in der Reihung |
Aufwand der binären Suche O(log2(anzahl)) |
Aufwand der sequenziellen Suche O(anzahl) |
mittlerer Aufwand von QuickSort O(anzahl * log2(anzahl)) |
Aufwand der einf. Sortierverfahren O(anzahl2) |
| 15 | 4 | 15 | 60 | 225 |
| 200 | 8 | 200 | 1 600 | 40 000 |
| 2 000 | 11 | 2 000 | 22 000 | 4 000 000 |
| 20 000 | 15 | 20 000 | 300 000 | 400 000 000 |
| 100 000 | 17 | 100 000 | 1 700 000 | 10 000 000 000 |
| 1 000 000 | 20 | 1 000 000 | 20 000 000 | 1 000 000 000 000 |
Aus der Tabelle wird deutlich, dass das Sortieren eines Datenbestands (insbesondere mit einfachen Verfahren) nur lohnt, wenn selten sortiert und dazwischen viel mit der binären Suche auf die Daten zugegriffen wird oder das Suchen besonders schnell gehen muss (und vorher Zeit zum Sortieren bleibt). Ändern sich die Daten häufig und wird nur gelegentlich gesucht, ist die sequenzielle Suche insgesamt schneller, weil auf das aufwändige Sortieren verzichtet werden kann.
zum Seitenanfang / zum Seitenende
Sortieren anderer primitiver Datentypen (int, char, boolean)
Im vorstehend angegeben Programm wurden Kommazahlen (double) sortiert. Sollen statt dessen 'nur' Ganzzahlen sortiert werden (und diese nicht in die Variablen oder Komponenten vom Typ double eingefüllt werden, sondern wirklich als int behandelt werden), müssen bei der Reihung und allen Hilfsvariablen für herausgenommene Werte (insbesondere in tausche sowie beim zwischenspeicher in einSort oder beim pivot-Element in QuickSort) die Typen verändert werden. Das Ordnungszeichen '<' gilt hingegen auch bei int, long und auch zwischen Schriftzeichen (char), die nach ihrem ANSI-Wert sortiert werden.
Während in anderen Programmiersprachen bekannt ist, dass der boolean-Wert false meist durch 0 = (0000 0000)2 und der Wert true entweder durch 1 = (0000 0001)2 oder -- bei anderen Sprachen -- durch (1111 1111)2 = -1 dargestellt wird, ist dadurch dort eine numerische Ordnung der Wahrheitswerte definiert. Java gibt aber nicht bekannt, wie die Wahrheitswerte kodiert werden und kennt und erlaubt keine Ordnungsrelation zwischen true und false, sodass Wahrheitswerte als booleans in Java nicht direkt sortiert werden können (höchstens ihre String-Repräsentationen durch die Wörter "true" und "false" oder mit eigener Vergleichsmethode, s.u.).
Im folgenden wird der Anfang der Klasse und beispielhaft wieder die Methode minSort mit den farbigen, unterstrichenen
Typ-Änderungen für int bzw. char gezeigt. Die Indizes bleiben natürlich immer (nicht-negative) Ganzzahlen!
|
public class Sort_2012_int // = Sortieren (und Suchen) von ganzen
Zahlen; www.r-krell.de { int [] reihe = new int [200]; // Original, wird erzeugt, sortiert & ausgegeben int anzahl = 0; // Füllgrad der Reihung(en) reihe (und backup) private void tausche (int i, int j) // tauscht die Inhalte(!), // die in der reihe an den Positionen i und j stehen/standen { int hilfe = reihe[i]; reihe[i] = reihe[j]; reihe[j] = hilfe; } public void minSort() // Sortieren durch Auswahl -- hier des jeweils kleinsten Elements |
|
public class Sort_2012_char // = Sortieren (und Suchen) von Schriftzeichen;
www.r-krell.de { char [] reihe = new char [200]; // Original, wird erzeugt, sortiert & ausgegeben int anzahl = 0; // Füllgrad der Reihung(en) reihe (und backup) private void tausche (int i, int j) // tauscht die Inhalte(!), // die in der reihe an den Positionen i und j stehen/standen { char hilfe = reihe[i]; reihe[i] = reihe[j]; reihe[j] = hilfe; } public void minSort() // Sortieren durch Auswahl -- hier des jeweils kleinsten Elements |
zum Seitenanfang / zum Seitenende
Sortieren von Texten (Strings)
Sollen erstmals Zeichenketten sortiert werden, befürchten Schülerinnen und Schüler erfahrungsgemäß, dass hier viele Sortiervorgänge nötig werden: Zuerst sollen bis zu 26 Packen der Texte mit jeweils gleichem Anfangsbuchstaben angelegt werden, danach soll innerhalb der Packen auf gleiche Weise nach dem zweiten, schließlich ebenso nach dem dritten, vierten,.. usw. Buchstaben sortiert werden, bis das gewünschte Ergebnis einer lexikografischen Reihenfolge (=wie im Wörterbuch) erreicht ist. Obwohl es sich lohnt, diesem Gedanken nach zu gehen, überrascht es, wenn man zeigt, dass es auch ohne Zerteilen geht, wenn man mit einem stabilen(!) Sortierverfahren zunächst z.B. die gesamte Reihung nur nach dem 20. Schriftzeichen sortiert, danach die so vorsortierte reihe nur nach dem 19. Zeichen, danach nach dem 18., 17., .. usw. und erst ganz zum Schluss nach dem Anfangsbuchstaben. (Was man unter der "Stabilität" eines Sortierverfahrens versteht, ist weiter oben am Ende des Kapitels "Erweiterungen zur Analyse der Sortier-Verfahren" definiert!)
Aber selbst dieses Vorgehen ist unnötig umständlich, weil man einfach von der in Java enthaltenen Methode compareTo Gebrauch machen kann, die die lexikografische Anordnung von Strings beherrscht (zumindest im Wesentlichen, weil sie zum Vergleich automatisch die ASCII- bzw. ANSI-Werte der Buchstabentabelle heranzieht und daher nationale Sonderzeichen und Umlaute stets nach hinten verfrachtet). Man muss nur wissen, dass diese Methode einen (Ganz-)Zahlenwert liefert, der kleiner, gleich oder größer als Null ist -- je nach Anordnung der Zeichenketten. So ist/sind
Damit hat auch das Sortieren von Texten seinen Schrecken verloren. Neben den wieder wie oben nötigen Typ-Änderungen muss nur das
Ordnungszeichen zwischen Reihungselementen durch die compareTo-Methode ersetzt werden (während eventuelle Vergleiche von Indexzahlen
wie bei i < anzahl natürlich weiter mit '<' funktionieren):
|
public class Sort_2012_string // = Sortieren (und Suchen) von Zeichenketten;
www.r-krell.de { String [] reihe = new String [200]; // Original, wird erzeugt, sortiert & ausgegeben int anzahl = 0; // Füllgrad der Reihung(en) reihe (und backup) private void tausche (int i, int j) // tauscht die Inhalte(!), // die in der reihe an den Positionen i und j stehen/standen { String hilfe = reihe[i]; reihe[i] = reihe[j]; reihe[j] = hilfe; } public void minSort() // Sortieren durch Auswahl -- hier des jeweils kleinsten Elements |
Es ist ärgerlich, wenn man zum Sortieren verschiedener Typen immer wieder ein nur an wenigen Stellen abgeändertes, aber neues Programm braucht, obwohl der verwendete Algorithmus grundsätzlich gleich ist. Der folgende Abschnitt zeigt eine Möglichkeit, ein allgemeines Sortierprogramm für alle Typen zu schreiben, das außerdem sogar beliebig komplexe Typen aufnehmen und sortieren kann.
zum Seitenanfang / zum Seitenende
Sortieren beliebiger Objekte nach wählbarem Sortierkriterium
Interessanter wird die Sache, wenn eigene Objekte sortiert werden sollen -- beispielsweise Autos, die ein Nummernschild haben, schon eine bestimmt Zahl von Kilometern gefahren sind, die ein Schiebedach haben oder nicht, deren Motorleistung in kW mit einer Nachkommastelle angegeben wird und die natürlich von einem Hersteller stammen und von einem bestimmten Typ sind. Möchte man mehrere Autos in einer Reihung verwalten, so soll es möglich sein, diese Reihung z.B. nach Autos mit oder ohne Schiebedach zu sortieren, oder alle Autos aufsteigend nach ihrer Leistung zu ordnen, bzw. für eine andere Suche die Autos nach dem Nummernschild oder nach ihrer Marke zu sortieren. Das Sortierkriterium bzw. der Sortierschlüssel kann dabei mal eine Ganzzahl, eine Kommazahl, ein Wahrheitswert oder ein Text sein!
Um jetzt nicht -- wie oben, grün und blau unterlegt -- vier oder fünf verschiedene Sortiermethoden schreiben zu müssen, muss einmal der Elementtyp allgemein angegeben werden und muss zweitens die Ordnungsrelation einheitlich geschrieben werden können.
Deshalb schlage ich vor, zunächst in einem Interface TypMitVgl einen allgemeinen Objekttyp zu versprechen, der -- in Anlehnung an das oben vorgestellte Java-eigene compareTo bei Strings -- über eine selbst zu schreibende Methode vergleicheMit verfügt, mit dem zwei Elemente dieses "Typs mit Vergleichsmöglichkeit" ihre Reihenfolge definieren. Ein zusätzlicher Parameter dient zur Auswahl des gewünschten Sortierkriteriums. Hier wird ein Buchstabe als Parameter angegeben; ab/seit Java 1.7 können auch Zeichenketten als Auswahltyp in switch-case-Anweisungen verwendet werden. Im Interface kann natürlich noch nicht festgelegt wqerden, welche Auswahlbuchstaben sinnvoll sind, weil das von der späteren konkreten Implementation abhängt. Angemerkt sei allerdings, dass prinzipiell auch die Java-Methode compareTo nach Bedarf überschrieben werden könnte und Java über ein Interface Comparable verfügt. Weil dort aber keine Auswahl verschiedener Kriterien vorgesehen ist, bleibe ich bei meinem Vorschlag.
Weil die Ordnungsrelation bzw. die Methode vergleicheMit zum einzelnen Element gehört, das sich mit einem anderen vergleichen kann, muss sie auch in der Objektklasse -- z.B. dem Auto -- notiert sein. Das Sortiertkriterium ist hingegen eher eine Eigenschaft der Reihung, die nach einem bestimmten Sortierschlüssel geordnet ist (oder noch nicht). Wichtig ist, dass das Sortierkriterium in dieser Klasse von verschiedenen Methoden genutzt werden muss: vom Sortieren z.B. ebenso wie vom Suchen (denn eine binäre Suche nach einer bestimmten Eigenschaft, etwa der Motorleistung, funktioniert nur, wenn zuvor beim letzten Sortieren gerade nach der Motorleistung sortiert wurde, also sortKrit='l' festgelegt wurde). sortKrit ist daher ein zur Reihung reihe gehöriges Attribut (wie anzahl) und muss daher in der Klasse mit reihe stehen. Natürlich muss es auch eine Möglichkeit oder eine Methode geben, das Sortierkriterium von außen zu setzen oder abzuändern (und vielleicht auch auszulesen). Genauso muss es natürlich oben und im Folgenden Methoden geben, um die Ganzzahlreihung, die Buchstabenreihung, die Textreihung oder die Autoreihung mit Ganzzahlen, Schriftzeichen, Zeichenketten oder Autos zu füllen. Dass dazu ein Konstruktor der Klasse Auto nützlich wäre, versteht sich von selbst. Die Auszüge in den farbig unterlegten Rahmen geben eben keine vollständigen Klassen an, sondern beschränken sich auf ein Sortierverfahren.
Diese Überlegungen führen dann etwa zu folgenden drei getrennten Dateien (Interface und zwei Klassen) für das erwähnte
Autobeispiel:
| public interface TypMitVgl { public double vergleicheMit (TypMitVgl anderer, char sortKrit); } |
| public class Auto implements TypMitVgl { String nummer; // z.B. "D~~-AD 2013" int gefahreneKm; // z.B 23500 boolean mitSchiebedach; // z.B. false double leistungInKW; // z.B. 84.5 String typ; // z.B. "Opel Astra" public double vergleicheMit (TypMitVgl anderesAuto, char sortKrit) { switch (sortKrit) { case 'n' : return (nummer.compareTo(((Auto)anderesAuto).nummer)); // "A~~-XY ~432" vor "AB~-C ~~40" case 'k' : return (gefahreneKm - ((Auto)anderesAuto).gefahreneKm);// 1250 km vor 33000 km case 's' : if (mitSchiebedach == ((Auto)anderesAuto).mitSchiebedach) { return (0); } else if (mitSchiebedach) { // Auto mit Schiebedach return (-1); // vor anderem Auto ohne } // Schiebedach else { return (1); } case 'l' : return (leistungInKW - ((Auto)anderesAuto).leistungInKW); // 40 kW vor 120 kW case 't' : return (typ.compareTo(((Auto)anderesAuto).typ)); // "Ford Ka" vor "Opel Astra" default : return (0); } } } |
| public class Sort_2013 // = Sortieren von beliebigen Objekten vom TypMitVgl, z.B. Autos // R. Krell, www.r-krell.de { TypMitVgl [] reihe = new TypMitVgl [200]; // Original, wird erzeugt, sortiert & ausgegeben int anzahl = 0; // Füllgrad der Reihung reihe char sortKrit = '?'; // Sortierkriterium; anfangs nocht nicht festgelegt private void tausche (int i, int j) // tauscht die Inhalte(!), // die in der reihe an den Positionen i und j stehen/standen { TypMitVgl hilfe = reihe[i]; reihe[i] = reihe[j]; reihe[j] = hilfe; } public void minSort() // Sortieren durch Auswahl -- hier des jeweils kleinsten Elements { int minStelle; for (int durchg =0; durchg < anzahl-1; durchg++) { // aufsteigend, da kleine Elemente nach vorne kommen minStelle = durchg; for(int i=durchg+1; i<anzahl; i++) { if (reihe[i].vergleicheMit(reihe[minStelle], sortKrit) < 0) { minStelle = i; } } tausche (minStelle,durchg); // kleinstes Element nach vorne tauschen } } ... |
Lässt man weitere Typen das Interface TypMitVgl implementieren, d.h. schreibt dafür eine vergleicheMit, kann man für alle solche Typen die unveränderte Klasse Sort_2013 verwenden und braucht dort nichts mehr zu ändern. Allerdings ist die reihe damit nicht mehr wirklich typsicher:
Würden auch Personen (mit Namen, Alter und Gehalt) das Interface TypMitVgl verwirklichen bzw. implementieren, könnte auch eine Person statt eines Autos versehentlich den Weg in die reihe finden und dort zusammen mit Autos gespeichert werden, ohne dass Java das merkt (weil die Inhalte von reihe nur vom TypMitVgl abgleitet sein müssen und das ja zutrifft). Beim Sortiervorgang gibt es dann aber vermutlich Probleme, weil die Sortierkriterien von Autos nicht auf Personen passen. Im weiß und grün bzw. blau unterlegten Text hätte der Java-Compiler gar nicht zugelassen, dass ein Wert von einem anderen als dem angegebenen Typ in die reihe gelangt (so kann etwa ein Text nicht in eine Reihung von Kommazahlen gefüllt werden).
Seit Java 1.5 gibt es inzwischen die Möglichkeit, so genannte generische Typen zu verwenden, d.h. an eine Klasse bzw. ein entsprechendes Objekt erst zur Laufzeit einen bestimmten Elementtyp zu übergeben, der dann verwendet werden muss. So würde beim Sortieren von Autos beim Erzeugen eines Objekts der Klasse Sort_2013_gen in spitzen Klammern mitgeteilt, dass von diesem Objekt sortdemo nur Autos aufgenommen und sortiert werden sollen. So würde etwa in der (für Autos umgearbeiteten) Oberfläche statt Sort_2012 sortdemo = new Sort_2012; (vgl. oben im Kapitel "Entwurf einer Swing-Oberfläche" die rote Ergänzung im dritten Bildschirmfoto vom Java-Editor) jetzt Sort_2013_gen<Auto> sortdemo = new Sort_2013_gen<Auto>; stehen. Damit würde Typsicherheit erreicht und es könnten nicht mehr Äpfel mit Birnen bzw. Autos mit Personen vermischt und verglichen werden. Leider funktionieren einzelnen Variablen und verschiedenen dynamischen Datentypen mit solchen in spitzen Klammern angegebenen Typen, aber aus übergebenen Typen können keine statischen Reihungen erzeugt werden, wie folgende Fehlermeldung zeigt:
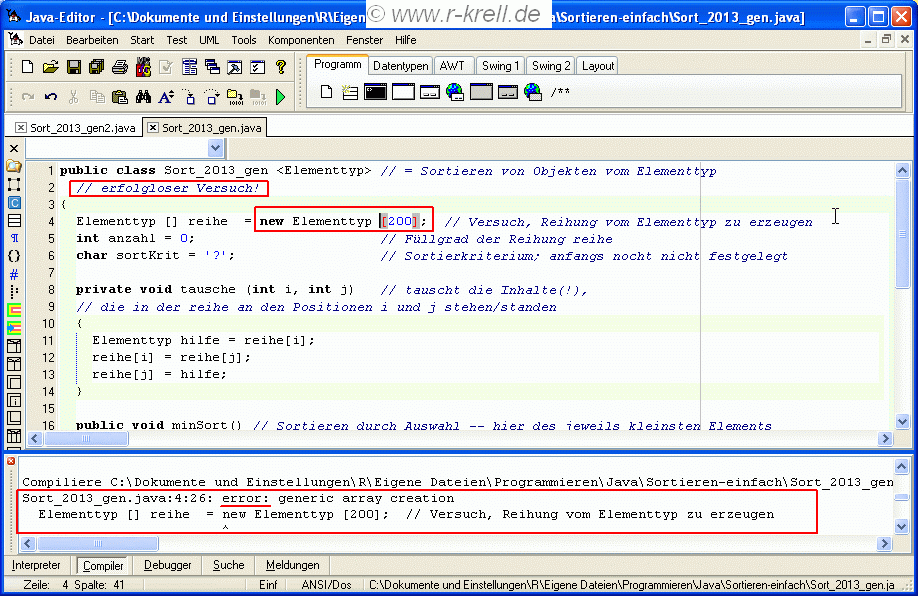
Allerdings muss man trotzdem nicht ganz auf Typsicherheit verzichten: Denn mit dem allgemeinen Typ Object, der als Obertyp für alle in Java erzeugten und erzeugbaren Typen gilt (also auch Obertyp z.B. von Auto oder Integer ist), lässt sich problemlos eine Reihung erzeugen. Das folgende Bild zeigt den erfolgreichen Versuch. Zwar muss dann in Zeile 11 eine Typanpassung ('type cast') auf den Elementtyp vorgenommen werden, der theoretisch -- wenn in der reihe andere Elemente stünden -- zu Fehlern führen könnte. Aber deswegen gibt's nur eine Warnung, keinen Java-Fehler. Das Programm lässt sich trotz der Warnung kompilieren und ausführen. Und dass in Zeile 24 nochmal eine Typanpassung auf TypMitVgl vorgenommen werden muss (weil der allgemeine Typ Object natürlich nicht die von uns definierte Methode vergleicheMit enthält), führt nicht mal mehr zu einer Warnung. Noch geschickter wäre es übrigens, wie oben im blass-pinkfarbig unterlegten Sort_2013 auch im Folgenden die reihe in Zeile 4 statt vom Typ Object direkt von und mit TypMitVgl zu erzeugen. Dann entfiele die Notwendigkeit der zweiten Typanpassung in Zeile 24:
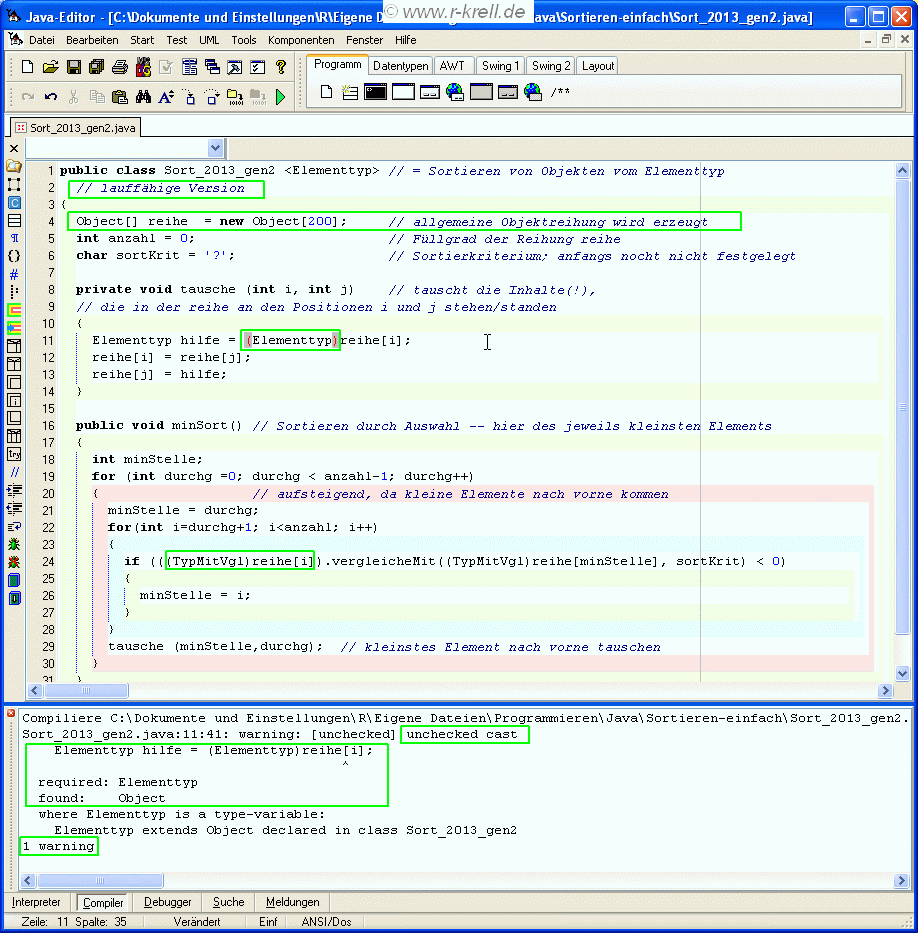
Soll ein Objekt der Klasse Sort_2013_gen2 später etwa auch zur Verwaltung von Autos verwendet werden können, die einzeln in die reihe kommen, empfiehlt sich an Stelle der ganz oben im Abschnitt 'Reihung und Hilfsmethoden' mal definierten Methode fülleZufällig eine Methode wie public void hängeAn (Elementtyp inhalt) { anzahl++; reihe[anzahl] = inhalt; }, die mit einem einzelnen übergebenen Element (z.B. einem Auto, wenn Auto der Elementtyp ist) den gefüllten Teil der Reihung vergrößert. Wird dann in der Oberfläche, wo die Daten des Autos eingegeben wurden, (oder einem anderen aufrufenden Programm) etwa Sort_2013_gen2<Auto> sortdemo = new Sort_2013_gen2<Auto>; definiert und erzeugt, so lassen sich dann mit sortdemo.hängeAn (a2); wirklich nur Autos in die Reihe einfügen. Wäre a2 von irgend einem anderen Typ, würde die Oberfläche nicht kompiliert! Die Typsicherheit wird also überwacht bzw. garantiert.
Wer sich außerdem für generische Typen bei dynamischen Datenstrukturen interessiert, sei auf den Anhang 3 (Seiten 27 bis 39) meines Referats über Keller und Schlangen, erreichbar über die Seite e) von "Informatik mit Java" verwiesen, wo vollständige Programmtexte (auch mit ebenfalls typisiertem Interface) angegeben und erläutert sind. Auf Seite 30 ist dort auch der Hinweis zu finden, dass Reihungen (arrays) und die (halb-)dynamische Java-eigene ArrayList nicht mit übergebenen Typen erzeugt werden können -- der gerade in Sort_2013_gen2 vorgestellte mögliche Umweg über eine Object- oder TypMitVgl-Reihung ist dort allerdings noch nicht erwähnt. Weil bei den dynamischen Datentypen wie Keller oder Schlange nicht über einen Index wahfrei auf jedes gespeicherte Element zugegriffen werden kann, kann in den dynamischen Datenstrukturen jedoch nicht mit den hier vorgestellten Verfahren sortiert werden.
zurück zur Informatik-Hauptseite
(Die anderen „Informatik mit Java"-Seiten werden am besten auch dort ausgewählt)