 Die Überschriften a) bis
e) verweisen auf die vorhergehenden Seiten, die Überschrift g) auf die folgende Seiten:
Die Überschriften a) bis
e) verweisen auf die vorhergehenden Seiten, die Überschrift g) auf die folgende Seiten:| www.r-krell.de |
| Webangebot für Schule und Unterricht, Software, Fotovoltaik und mehr |
Willkommen/Übersicht > Informatik > Informatik-Seite f)
Teil f): Abstrakter Datentyp Baum
(z.B. als binärer Sortier-, AVL- oder Rechen-Baum
sowie als vielfach-verzweigter Spielbaum)
 Die Überschriften a) bis
e) verweisen auf die vorhergehenden Seiten, die Überschrift g) auf die folgende Seiten:
Die Überschriften a) bis
e) verweisen auf die vorhergehenden Seiten, die Überschrift g) auf die folgende Seiten:
a) Grundlegendes zu Java, benötigte Software (inkl. Downloadadressen) und
Installation
b) Erste Java-Programme (u.a. Autorennen u. Aufzug) sowie Verweise (Links) auf fremde
Java-Seiten
c) Sortieren und Suchen in Java sowie grafische Oberflächen mit der
Java-AWT
d) Adressbuch- und Fuhrpark-Verwaltung sowie Datei-Operationen mit Java
e) Lineare abstrakte Datentypen Keller, Schlange, Liste und Sortierte Liste (sowie
Tiefen- u. Breitensuche)
f) Abstrakter Datentyp Baum
g) Abstrakter Datentyp Graph: Typische Graphenprobleme, Wegsuche, Breiten- und
Tiefensuche.
h) Bau eines Compilers Java -> 1_AMOR (Syntaxdiagramm, Scanner, Parser, Variablentabelle,
Codeerzeuger)
Eine vollständige Übersicht aller Java-Seiten gibt's auf der Informatik-Hauptseite!
zum Seitenanfang / zum Seitenende
Idee
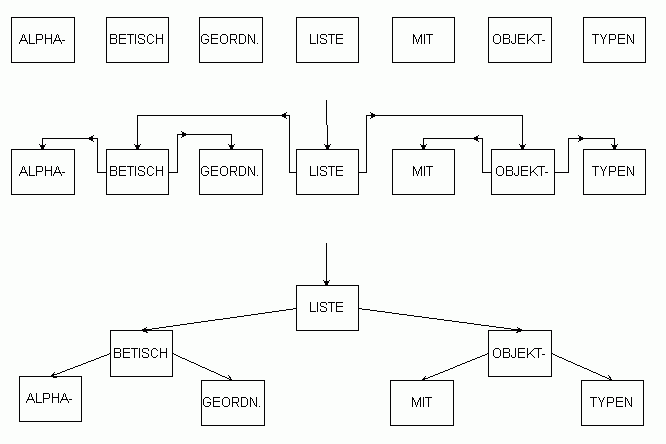
Das auf der letzten Seite („Informatik mit Java", Teil e) - vierter ADT) bei den sortierten Listen erwähnte Problem, dass der Computer auch in einer sortierten Liste nicht rascher als in einer unsortierten Liste suchen kann, weil er sich trotzdem immer von Anfang an Element um Element entlang der Verkettung weiter hangeln muss, legt eine andere Art der Verkettung nahe: Für das Halbierungsverfahren (binäre Suche) wäre es günstiger, direkt zum mittleren Element der geordneten Liste springen zu können, dann von dort wahlweise zur Mitte der ersten oder zweiten Hälfte gelangen zu können, usw. Verschiebt man die Knoten so, dass die Verkettungspfeile wieder gerade gezeichnet werden können, führt die zur Baumstruktur, wo jeder Knoten bis zu zwei Nachfolger hat. Das oberste (mittlere) Element wird als Wurzel bezeichnet.
zum Seitenanfang / zum Seitenende
Knoten und Elemente
Neben den beiden Zeigern li und re auf die Nachfolge-Knoten (oder null) enthält jeder Knoten als Inhalt ein beliebiges sortierbares Objekt,
| // Java-Baum-Programm, für IF12M -- Krell, 2.6.04, 10.8.04 -- www.r-krell.de public class F_Knoten { F_ObjektMitOrdnung inhalt; // gespeicherte Informationen F_Knoten li, re; // Zeiger auf andere Knoten im Baum. public F_Knoten (F_ObjektMitOrdnung neuerInhalt) // Konstruktor für neuen Knoten.. { // .. erleichtert das Erzeugen, da neuer Knoten immer als Blatt inhalt = neuerInhalt; li = null; // d.h. beide Nachfolger eines neuen Baumknotens re = null; // sind zunächst null! } } |
d.h. der inhalt ist ein Objekt, für das die Ordnungsrelation vergleicheMit definiert ist. Genau wie auf der Seite „Informatik mit Java", Teil e) lässt sich dies über ein Interface sicher stellen: Aus Bequemlichkeit ist hier direkt noch ein Anzeige- bzw. Ausgabemethode angefügt, die von anderen Objekten (z.B. einer Oberfläche aus) aufgerufen werden kann.
| // Java-Baum-Programm, für IF12M -- Krell, 2.6.04, 10.8.04 -- www.r-krell.de public interface F_ObjektMitOrdnung // wie E_ObjektMitOrdnung + zeigeObjekt { public double vergleicheMit (Object anderes, char sortKrit); // Hiermit wird -- ähnlich wie durch compareTo für Strings -- die Reihenfolge // zweier Objekte festgelegt. Anders als bei der vordef. Java-Methode bzw. Com- // parable kann noch ein Sortierkriterieum gewählt werden. Speichert man z.B. // Schüler mit Namen, Vornamen, Zeugnisnote und Alter, so soll mit dem zu über- // gebenden Buchstaben ausgesucht werden, welches Datenfeld der Sortierschlüssel // ist. Bei sortKrit='v' könnte z.B. alphabet. nach Vornamen sortiert werden, // während bei 'z' Schüler nach ihren Zeugnisnoten verglichen/geordnet werden. // Details müssen natürlich bei den konkreten Klassen formuliert werden, die // dieses Interface implementieren. // a.vergleicheMit(b, sortKrit) < 0 bedeutet a<b; ==0 <=> a=b; >0 <=> a>b // bezüglich des gewählten Sortierkriteriums. public String zeigeObjekt (); // gibt die wesentlichen Informationen des Elements in einer Textzeile aus } |
Eine mögliche Inhalts- bzw. Element-Klasse, die dieses Interface implementiert, ist die schon im Applet von sortierten Listen verwendete Klasse für Objekte mit zwei verschiedenen Datenfeldern, einem Text und einer Kommazahl:
| // Java-Baum-Programm, für IF12M -- Krell, 2.6.04, 10.8.04 -- www.r-krell.de public class F_BeispObjekt implements F_ObjektMitOrdnung, java.io.Serializable //Serializ. f. Datei-Op { String text; double zahl; public F_BeispObjekt (String wort, double kommazahl) { text = wort; zahl = kommazahl; } public double vergleicheMit (Object anderes, char sortKrit) { switch (sortKrit) { case 't' : return (text.compareTo( ((F_BeispObjekt)anderes).text )); case 'z' : return (zahl - ((F_BeispObjekt)anderes).zahl); default : return (0); } } public String zeigeObjekt () { return (text+"/"+zahl); } } |
Damit sind die Vorarbeiten erledigt: wir wissen jetzt, was in den Baum soll und wonach er sortiert wird. Nun können wir uns dem Aufbau des eigentlichen Baums zu wenden:
zum Seitenanfang / zum Seitenende
Die Klasse Sortierbaum -- Aufbau und Verwaltung des Baums
Zunächst soll noch mal ein Überblick gegeben werden, was der Sortierbaum enthalten und können soll. Dabei sind schon ein paar zusätzliche Methoden genannt, die für die Datenspeicherung nicht unbedingt nötig sind. Die Methoden istLeer, sortRein, zeigeGesucht und löscheGesucht haben natürlich genau den gleichen Kopf (die gleiche 'Signatur') wie die entsprechenden Methoden bei der sortierten Liste. Letztlich soll es dem Benutzer ja egal sein, ob der sortierte Datenspeicher mit einer Liste oder mit einem Baum realisiert wird. Beim Baum wird er sich allerdings über die raschere Ausführung der Methoden freuen können (vorausgesetzt, der Baum ist einigermaßen ausgewogen und nicht zur Liste entartet):
| // Java-Baum-Programm, für IF12M -- Krell, 12.7.04, 10.8.04 -- www.r-krell.de public class F_Sortierbaum { // ------------------- Eigenschaften bzw. Datenfelder --------------: F_Knoten wurzel; // "Zeiger" auf den obersten Knoten im Baum char sortKrit; // Sortierkriterium, nach dem der Baum aufgebaut wird // --------------------- Methoden ----------------------------------: public F_Sortierbaum (char sortierKriterium) // Konstruktor: legt neuen leeren Baum an { wurzel = null; sortKrit = sortierKriterium; } // ----------------------------------------------------------------- // die folgenden Methoden sind noch nicht funktionsfähig, sondern sollen // nach und nach „gefüllt" werden: public boolean istLeer () // prüft, ob der Baum ganz leer ist public void sortRein (F_ObjektMitOrdnung element) // erzeugt an richtiger Stelle neuen Knoten im Baum und füllt diesen mit element public F_ObjektMitOrdnung zeigeGesucht (F_ObjektMitOrdnung gesuchtesElement) // nennt das vollständige Element, das mit gesuchtesElement bzgl. sortKrit übereinstimmt public F_ObjektMitOrdnung löscheGesucht (F_ObjektMitOrdnung löschElement) // entfernt Knoten mit Übereinstimmung mit löschElement bzgl. sortKrit aus dem Baum // ----------------------------------------------------------------- // Die vorstehenden Methoden reichen zur Benutzung des Baums als sortierter Datenspeicher. // Zur zusätzlichen Übung können noch die im nachfolgenden Applet eingebauten Methoden // geschrieben werden: public int knotenZahl() // nennt die Anzahl der Knoten im Baum public int ebenenZahl() // nennt die Anzahl der Ebenen im Baum public String lwrAusgabe () // gibt die Elemente linear in einem String in LWR-Reihenfolge („Inorder") aus public String wlrAusgabe () // gibt die Elemente linear in einem String in WLR-Reihenfolge („Preorder") aus public String lrwAusgabe () // gibt die Elemente linear in einem String in LRW-Reihenfolge („Postorder") aus public String ebenenweiseAusgabe() // gibt die Elemente linear in einem String aus wie zeilenweise aus dem Baum gelesen public String aufDisk1 (String dateiName) // speichert Baum in einer Datei mit angegebenem Namen und meldet Erfolg/Misserfolg public String vonDisk1 (String dateiName) // holt Baum aus der Datei mit angegebenem Namen und meldet Erfolg/Misserfolg, // wobei die Struktur erhalten werden soll, d.h. genau der mit aufDisk1 gespeicherte Baum // wieder hergestellt werden soll public String aufDisk2 (String dateiName) // speichert Baum in einer Datei mit angegebenem Namen und meldet Erfolg/Misserfolg public String vonDisk2 (String dateiName) // holt Baum aus der Datei mit angegebenem Namen und meldet Erfolg/Misserfolg, // wobei zwar alle Elemente des mit aufDisk1 gespeicherten Baums wieder hergestellt // werden sollen, der Baum jetzt aber optimale (ausgewogene) Form haben soll |
zum Seitenanfang / zum Seitenende
Ehrgeizige Leserinnen und Leser sollten jetzt die Lektüre dieser Seite abbrechen, und selbst die skizzierten Methoden schreiben. Als Tipp sei noch erwähnt, dass sich rekursive Methoden gut eignen. Zur Motivation können Sie hier noch ausprobieren, wie die Methoden funktionieren sollen:
Interaktiver Test eines Sortier-Baums (mit Java-Applet)
Es werden aus Anwendersicht die gleichen Methoden wie bei der sortierten Liste benutzt, aber intern wird eine andere Speicherstruktur verwendet!
Wer mit seiner Implementation fertig ist, findet auf der folgenden Extraseite zu einigen, aber nicht zu allen Methoden die ausgeführten Quelltexte. Und durch die Extraseite soll erreicht werden, dass der vorzeitige Blick auf eine mögliche Lösung die eigene Kreativität nicht zu früh bremst! Also bitte erst nach eigenen ernsthaften Überlegungen nachsehen:
Java-Quelltext der Klasse Sortierbaum (Auszüge)
Im Baum muss man zum Einsortieren, Finden oder Entfernen eines Elements höchstens einmal von der Wurzel entlang eines Astes bis zur richtigen Stelle nach unten gehen, d.h. höchstens bis zur untersten Ebene gelangen. Beim ausgewogenen oder ausgeglichenen Baum ist die Ebenzahl ~ log2(Elementzahl). Oben wurde mit den Methoden aufDisk2 und vonDisk2 zwar schon eine Möglichkeit angedeutet, für einen ausgewogenen Baum zu sorgen (wie Sie im Applet auch ausprobieren konnten oder können). Allerdings ist diese Art der Strukturverbesserung selbst recht aufwändig. Inzwischen kennt man offenbar verschiedene Möglichkeiten einer geschickteren Höhenbalancierung; das älteste und wohl bekannteste Verfahren ist das von Adelson-Velskij und Landis 1962 erdachte AVL-Verfahren, das auf einer Reihe fremder Webseiten (die in neuen Fenstern geöffnet werden) studiert werden kann:
|
Applets für
AVL-Bäume |
||
| Binär- und AVL-Bäume | Wirtschafts-Uni Wien | Bebilderte Beschreibung aller wichtigen normalen und der AVL-Baumoperationen mit Java-Quelltext und Applet |
| OOP-Projekt AVL-Bäume | FH Regensburg | Grafisch gelungenes Applet mit dokumentiertem Quelltext |
| AVL-Baum | Uni/TH Karlsruhe (ALFI) | Applet für AVL-Baum-Operationen mit kurzer Beschreibung |
| AVL-Tree | TU Braunschweig & Uni Mannheim | Java-Applet (der dort angegeben Link zu Quelltexten funktioniert aber nicht mehr) |
Das AVL-Verfahren nimmt schon beim Aufbau des Baums (also in sortRein, aber nur innerhalb des gerade besuchten Astes) erforderlichenfalls eine strukturverbessende Ausgleichsoperationen vor (von denen es die vier Typen LL, RR, RL und LR gibt). Trotzdem behält sortRein den logarithmischen Aufwand und der so aufgebaute Baum garantiert auch für die anderen Operationen logarithmischen Aufwand - wenngleich mit einem geringfügig größeren Vorfaktor als beim ideal ausgewogenen Baum. Auf weitere AVL-Details soll hier aber nicht eingegangen werden; in der Literatur und auf den vorstehend genannten und vielen weiteren Internetseiten von Universitäten bzw. von Uni-Dozentinnen und -Dozenten findet man mehr. Hier reicht, dass Bäume die idealen Speicher für sortierte Daten sind und ihre Aufgabe gut und zuverlässig erfüllen.
Abschließend sei noch bemerkt, dass in der Bibliothek der Java-SDK seit 1.2 auch ein Sortierbaum mitgeliefert wird, nämlich TreeMap, der offenbar auch über eine automatische Balancierung verfügt, weil für die Zugriffe auf seine Elemente logarithmischer Aufwand garantiert wird. Für Einzelheiten wird auf die Java-Dokumentation verwiesen.
zum Seitenanfang / zum Seitenende
Bäume zum Rechnen
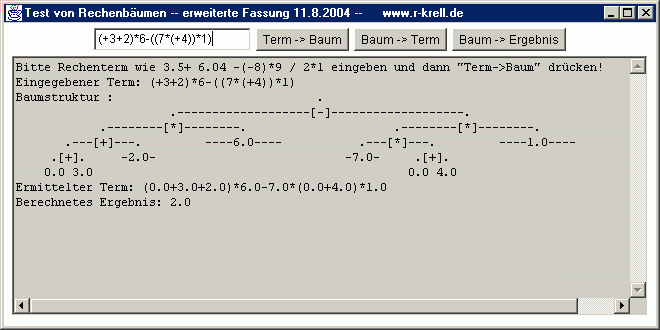
Binäre Bäume (also solche, wo jeder Knoten maximal zwei Nachfolger hat) können aber nicht nur als sortierte Datenspeicher verwendet werden. Sie eigenen sich auch, um etwa die im Mathematikunterricht der Klassen 5 bis 7 verwendeten Rechenbäume zu realisieren. Beim Rechenbaum geht es um die Hierarchie der auszuführenden Rechenoperationen in einem Term - damit wird z.B. „Punkt- vor Strichrechnung" visualisiert: An einem Knoten mit einem Rechenzeichen hängen die durch die Operation verknüpften Zahlen bzw. (Unter-)Terme. Deswegen dürfen die Zahlen natürlich nicht im Baum nach ihrem Wert sortiert angeordnet werden - es handelt sich also nicht um einen Sortierbaum! - sondern müssen entsprechend ihrer Stellung im Term bzw. der Priorität der damit ausgeführten Verknüpfung in den Baum (s.u., Aufgabe 3c)).

Wer sich selbst an diesem einfachen Rechenbaum versuchen will, findet hier einige vorbereitete Javadateien (mit geeigneten Objekten und einer Oberfläche) zum Herunterladen. Letztlich gestartet werden muss Rb_Start.java mit der main-Methode, Ergänzungen sind aber nur in Rb_Rechenbaum.java nötig.
Download: Java-Texte rb_rechenbaum.zip (5 kB) für den einfachen Rechenbaum
Die Aufgabe sollte durchaus von einer Lk-Schülerin bzw. einem Lk-Schüler der 12 bewältigt werden können.
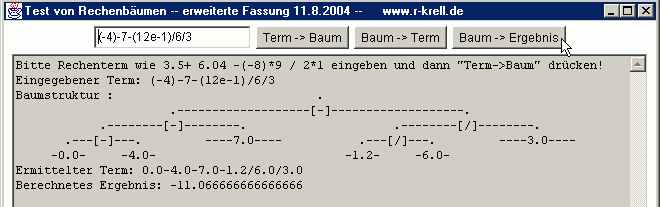
Lässt man hingegen auch Leerzeichen, Vorzeichen und echte Kommazahlen (ggf. noch
in wissenschaftlicher Schreibweise, d.h. mit Zehnerpotenzen) in der Eingabe zu, muss der Eingabe-String mit einem
Scanner in Sinneinheiten (Token) zerlegt werden. Der in der Java-SDK enthaltene StringTokenizer ist dazu
ungeeignet; die Dokumentation des dabei erwähnten StreamTokenizers ermutigte nicht gerade zu seiner
Verwendung. Mit den Ideen eines endlichen Automaten ist der Scanner letztlich nicht schwierig und kann schematisch
aus dem Automatengraph in Java übersetzt werden.
Deutlich anspruchsvoller war der Aufbau des Baums, wobei Klammern am besten rekursiv einen neuen (Teil-)Baum starten.
Die Prioritäten sollten aber systematisch geklärt werden -- eine Erweiterung des ad-hoc-Zugangs des
einfachen Rechenbaums ist wenig sinnvoll und endet vermutlich im Chaos. Ist der Baum einmal erzeugt, so ist die
Berechnung des Resultats dann zum Glück nicht schwieriger als beim einfachen Baum. Umständlicher ist es
wieder, aus dem aufgebautem Baum den Term zu erzeugen, wenn man nur unbedingt nötige Klammern ausgeben will.
Zunächst müssen von Hand Tabellen aufgestellt und schließlich in die Programmiersprache umgesetzt
werden, bei welchen der 32 Kombinationen eines Rechenzeichens im Knoten und den Rechenzeichen in seinem linken bzw.
rechten Nachfolger Klammern nötig sind bzw. auf Klammern verzichtet werden kann. Letztlich lässt sich aber
auch diese Herausforderung bewältigen, wobei unzulässige Eingaben nicht zum Programmabsturz, sondern zu
aussagekräftigen Fehlemeldungen führen sollten:




zum Seitenanfang / zum Seitenende
Spielbäume
 Abschließend sei noch
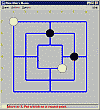
erwähnt, dass es nicht nur binäre Bäume gibt. Betrachtet man z.B. ein Zwei-Personen-Spiel wie etwa
Mühle, so kann der erste Spieler („Weiß") seinen ersten Stein auf eine von 24 leere Ecken oder
Kreuzungen setzten. Sollen in einem Baum die möglichen Stellungen des Spiels verwaltet werden, so gehen vom
Wurzelknoten (leeres Brett, Weiß am Zug) also 24 Verzweigungen zu den 24 möglichen Spielständen mit
einem weißen Stein aus, wobei dann Schwarz am Zug ist. Schwarz hat jetzt nur 23 Möglichkeiten, seinen
Stein zu setzten, bevor wieder Weiß am Zug ist. Es wird schnell klar, dass dieser Baum u.U. sehr viele Knoten
aufnehmen muss, und eben kein binärer Baum mehr ist. Statt zweier fester Zeiger li und re auf
die Nachfolger wie beim Binärbaum empfiehlt sich hier für jeden Knoten eine dynamische Liste auf die (je
nach Spielsituation ja oft unterschiedlich vielen) Nachfolge-Knoten.
Abschließend sei noch
erwähnt, dass es nicht nur binäre Bäume gibt. Betrachtet man z.B. ein Zwei-Personen-Spiel wie etwa
Mühle, so kann der erste Spieler („Weiß") seinen ersten Stein auf eine von 24 leere Ecken oder
Kreuzungen setzten. Sollen in einem Baum die möglichen Stellungen des Spiels verwaltet werden, so gehen vom
Wurzelknoten (leeres Brett, Weiß am Zug) also 24 Verzweigungen zu den 24 möglichen Spielständen mit
einem weißen Stein aus, wobei dann Schwarz am Zug ist. Schwarz hat jetzt nur 23 Möglichkeiten, seinen
Stein zu setzten, bevor wieder Weiß am Zug ist. Es wird schnell klar, dass dieser Baum u.U. sehr viele Knoten
aufnehmen muss, und eben kein binärer Baum mehr ist. Statt zweier fester Zeiger li und re auf
die Nachfolger wie beim Binärbaum empfiehlt sich hier für jeden Knoten eine dynamische Liste auf die (je
nach Spielsituation ja oft unterschiedlich vielen) Nachfolge-Knoten.
Tatsächlich überfordert aber bei den meisten Spielen der Aufbau des vollständigen Baums (selbst wenn man symmetrische Stellungen zusammenfasst) auch die schnellsten Rechner (sonst wäre das Spiel gegen den Computer auch langweilig, weil der Rechner bei vollem Überblick nicht verlieren würde). In der Praxis kann der Baum nur bis zu einer gewissen, geringen Tiefe aufgebaut werden und die Erfolgsaussichten jedes Zweiges müssen ohne genaue Kenntnis der Folgen durch mehr oder weniger gute heuristische Bewertungsverfahren abgeschätzt werden. In diesen Verfahren unterscheiden sich auch unterschiedliche Programme zum gleichen Spiel und zumindest bei geringer Baumtiefe haben auch menschliche Spielerinnen und Spieler so durchaus noch eine Chance gegen den Computer...
Können nach unterschiedlichen Zugfolgen gleiche Spielstände erreicht werden, die auch nur durch einen Knoten dargestellt werden, auf den von mehreren Stellen gezeigt wird, so erzeugt man Maschen und gibt die Gliederung in Ebenen auf: die neu entstandene Struktur ist dann kein Baum mehr, sondern wird als Graph bezeichnet. Graphen werden im Teil g) meiner Seiten „Informatik mit Java" behandelt.
zurück zur Informatik-Hauptseite
(Die anderen Java-Seiten werden entweder mit dem Menü hier am Seitenanfang oder
am besten auch auf der Informatik-Hauptseite ausgewählt)