Die
Überschriften a) bis f) verweisen auf die vorhergehenden Seiten, Überschrift h) auf die nachfolgende:| www.r-krell.de |
| Webangebot für Schule und Unterricht, Software, Fotovoltaik und mehr |
Willkommen/Übersicht > Informatik > Informatik-Seite g)
Teil g): Abstrakter Datentyp Graph
Die
Überschriften a) bis f) verweisen auf die vorhergehenden Seiten, Überschrift h) auf die nachfolgende:
a) Grundlegendes zu Java, benötigte Software (inkl. Downloadadressen) und
Installation
b) Erste Java-Programme (u.a. Autorennen u. Aufzug) sowie Verweise (Links) auf fremde
Java-Seiten
c) Sortieren und Suchen in Java sowie grafische Oberflächen mit der
Java-AWT
d) Adressbuch- und Fuhrpark-Verwaltung sowie Datei-Operationen mit Java
e) Lineare abstrakte Datentypen Keller, Schlange, Liste und Sortierte Liste (sowie
Tiefen- u. Breitensuche)
f) Abstrakter Datentyp Baum ([binärer] Sortierbaum, Rechenbaum, Spielbaum)
Übersicht über diese Seite :
g) Abstrakter Datentyp Graph
Folgende Seite:
h) Bau eines Compilers Java -> 1_AMOR (Syntaxdiagramm, Scanner, Parser, Variablentabelle,
Codeerzeuger)
Eine vollständige Übersicht aller Java-Seiten gibt's auf der Informatik-Hauptseite!
zum Seitenanfang / zum Seitenende
Auf der letzten Seite [„Informatik mit Java", Teil f): Bäume] wurde im Zusammenhang mit Spielbäumen schon erwähnt, dass bei Spielen mehrere Züge oder Wege zum gleichen Spielstand führen können. Eine allgemeine Struktur aus Knoten (engl.: vertex, plural vertices; [Eck-]Punkte, Spielstände,..) und beliebigen Kanten (engl.: edge; Verbindungen zwischen je zwei Knoten) heißt Graph.
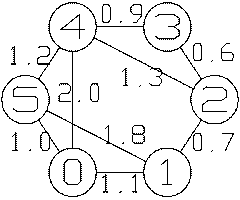
zum Seitenanfang / zum Seitenende
Repräsentation eines Graphen im Computer
Leider kann der Graph nicht als Bild in den Computer eingegeben werden. Vorhandene Graphenknoten und die verbindenden Kanten müssen den Möglichkeiten der Programmiersprache entsprechend mitgeteilt werden. Unter vielen Alternativen seien zwei wichtige Varianten hervorgehoben:
a) 
Adjazenzmatrix
Der Graph wird in Tabellenform gespeichert - entsprechend der auf der letzten Seite im Autoatlas zu findenden Entfernungstabelle, wobei am Rand aber nicht nur wichtige Städte, sondern jeweils alle Knoten des Graphen stehen. Zur Speicherung wird eine statische 2-dimensionale Reihung (2-dim. Array) verwendet. Nicht vorhandene Verbindungen werden mit einem besonderen Gewicht, z.B. mit der Zahl Unendlich für unendlich hohe Kosten bzw. unendlich große Entfernung, markiert. In der ausgedruckten grauen Tabelle steht an Stelle von Unendlich ebenso ein Strich wie für die Kosten/Entfernung, die jeder Knoten von sich selbst hat. Letzteres könnte man auch mit 0 angeben.
| // Java-Graphen-Programm, für IFL13M -- Krell,
11/04 + 7.12.04 + 12.3.05 public class Graf_Matrix { int knotenzahl = 0; double [][] kante; // in dieser 2-dim. Reihung ("Adjazenzmatrix") wird der Graph.. // .. bzw. werden seine Kanten gespeichert public void setzeKnotenzahl (int knZahl) { knotenzahl = knZahl; kante = new double [knotenzahl][knotenzahl]; for (int i=0; i < knotenzahl; i++) // Initialisieren: alle Kanten- { for (int j=0; j < knotenzahl; j++) { kante [i][j] = Double.POSITIVE_INFINITY; //-kosten auf Unendlich } } } public int holeKnotenzahl () { return (knotenzahl); } public void setzeKante (int von, int bis, double kosten) { kante [von][bis] = kosten; } public double holeKantenKosten (int von, int bis) { return (kante [von][bis]); } } |
zum Seitenanfang / zum Seitenende
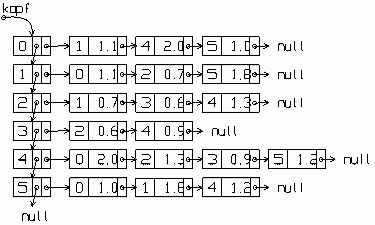b) Adjazenzliste
Gibt es viele Graphenknoten, aber nur relativ wenige Kanten, so steht sehr oft Unendlich in der Tabelle und nur wenige Einträge in der Adjazenzmatrix enthalten echte Informationen. Das ist Speicherplatzverschwendung, denn es reicht, für jeden Knoten nur die wirklich mit ihm unmittelbar verbundenen Nachbarknoten (mit dem jeweils zugehörigen Kantengewicht) einzutragen. Im Bild des Graphen sind ja auch nur Striche bzw. Pfeile für die tatsächlich vorhandenen Kanten eingezeichnet.
In Programmiersprachen wie Pascal bzw. Delphi, wo man selbst Zeigertypen definieren muss, ist es wichtig, die unterschiedlichen Listenknoten im linken Bild zu definieren und dazu passende Zeiger einzurichten. In Java enthält einfach die vertikale Liste selbstdefinierte Objekte, deren Bauplan vObjekt als Inhalt die Nummer des Knotens sowie eine Liste mit den Nachbarn vorsieht. Die Objekte hObjekt in jeder horizontalen Liste enthalten die Nummer des Nachbarknotens und das Kantengewicht. In Java kommt es also auf die Schaffung geeigneter Klassen für die Listenobjekte an, während man sich nicht um die Zeiger kümmern muss, sondern einfach fertige dynamische Listen (wie sie z.B. auf meiner Seite „Informatik mit Java", Teil e) beschrieben wurden) mit den üblichen Operationen verwendet:
| // Java-Graphen-Programm - R. Krell // 1. Inhalte für die vertikale Liste public class vObjekt { int nummer; // Nummer vom Graphenknoten Liste nachbarn; // (horizontale) Liste der Nachbarn (Liste wie auf Seite e)) public vObjekt (int i) // Konstruktor { nummer = i; nachbarn = new Liste (); // zunächst leere Liste } } |
| // Java-Graphen-Programm - R. Krell // 2. Inhalte für die horizontale Liste public class hObjekt { int nr; // Nummer vom Nachbarknoten double kosten; // Kantenkosten für die Kante zu diesem Nachbarn public hObjekt (int i, double k) // Konstruktor { nr = i; kosten = k; } } |
Die Adjazenzlisten-Struktur mit ihren Methoden hat dann beispielsweise folgendes Aussehen (wegen der durch die Kommentare langen Zeilen jetzt in voller Breite wieder gegeben - bitte notfalls den horizontalen Rollbalken Ihres Browsers verwenden, um auch die Zeilenenden zu sehen!):
// Java-Graphen-Programm - R. Krell
// Darstellung des Graphen mit Adjazenzlisten.
public class Graf_Listen
{
int knotenzahl = 0;
Liste vListe; // vListe = vertikale Liste aller Knoten
public void setzeKnotenzahl (int knZahl)
{
knotenzahl = knZahl;
vListe = new Liste(); // vListe = vertikale Liste aller Knoten
// Von jedem Knoten dieser vListe geht seitlich eine horizontale Liste ab. Eigentlich --
// weil sowieso für jeden Graphenknoten genau ein Knoten in der vListe angelegt wird --
// wäre eine Reihung für vListe praktischer
for (int i=0; i<knotenzahl; i++) // für jeden Graphenknoten i
{ // einen vKnoten in der vListe anlegen;
vListe.rein (new vObjekt(i)); // Nummer des Graphenknoten und zunächst
} // leere horizontale Nachbarliste speichern
}
public int holeKnotenzahl ()
{
return (knotenzahl);
}
public void setzeKante (int von, int bis, double kosten)
// Trägt eine Kante in die Listen ein:
{
vListe.anAnfang(); // Zunächst wird ab dem Anfang der vertikalen Liste ..
while (((vObjekt) vListe.zeige1()).nummer != von)
{ // .. der Knoten mit der Nummer von gesucht
vListe.weiter();
} // Dieser ist bei Schleifenende gefunden!
((vObjekt) vListe.zeige1()).nachbarn.anAnfang();
// Nachbarn von von
von Anfang an nach
bis durchsuchen:
while (!((vObjekt) vListe.zeige1()).nachbarn.istAmEnde())
{ // (Leider wird der Programmtext durch die vielen Type-Casts etwas lang)
if (((hObjekt) ((vObjekt) vListe.zeige1()).nachbarn.zeige1()).nr == bis)
{ // Falls es einen solchen Knoten schon gibt,
Object vergissEs = ((vObjekt) vListe.zeige1()).nachbarn.raus(); // rauswerfen: Kante wird
} // ersetzt (nicht zwei Kanten von -> bis erlaubt!)
((vObjekt) vListe.zeige1()).nachbarn.weiter();
}
((vObjekt) vListe.zeige1()).nachbarn.rein (new hObjekt(bis, kosten));
} // Und neue Kante in Gestalt eines Listeneintrags
// in die Nachbarliste einfügen
public double holeKantenKosten (int von, int bis)
{ // Nennt die Kosten der Kante von -> bis
vListe.anAnfang(); // Dazu vListe von Anfang an nach von durchsuchen
while (((vObjekt) vListe.zeige1()).nummer != von)
{
vListe.weiter();
} // Wenn von gefunden, ab von seitlich seine Nachbarn
((vObjekt) vListe.zeige1()).nachbarn.anAnfang(); // von Anfang an
while (!((vObjekt) vListe.zeige1()).nachbarn.istAmEnde()) // und höchstens bis zum Ende
{
if (((hObjekt) ((vObjekt) vListe.zeige1()).nachbarn.zeige1()).nr == bis)
{ // nach bis durchsuchen
return (((hObjekt) ((vObjekt) vListe.zeige1()).nachbarn.zeige1()).kantenKosten);
} // Falls gefunden, Kosten zurück geben und Ende
((vObjekt) vListe.zeige1()).nachbarn.weiter(); // sonst weiter suchen
}
return (Double.POSITIVE_INFINITY); // falls bisher nichts gefunden und zurück gegeben wurde,
} // ist die Kante
gar nicht da und ihr Wert Unendlich
}
Der Programmieraufwand für die dynamische Listendarstellung ist also größer als für die statische Matrix. In jedem Fall können wir jetzt einen Graphen im Computer speichern (auf der Seite „Informatik mit Prolog"wird übrigens der Graph auch in einer nicht befehlsorientierten Programmiersprache gespeichert). Hier geht es in den nächsten Abschnitten darum, mit dem Graphen zu arbeiten.
zum Seitenanfang / zum Seitenende
Einige typische Fragestellungen im Zusammenhang mit Graphen
In der Literatur der mathematischen Graphentheorie und in einschlägigen Informatikbüchern und -Vorlesungen werden häufig u.a. folgende Aufgaben für Graphen gestellt:
Manchmal werden auch - wie das schon bei Spannbäumen der Fall war, die nur noch eine Teilmenge der
ursprünglichen Kanten enthalten - bestimmte Teilmengen der Knoten (Independet Set, Vertex Cover, Cliquen) oder
der Kanten (Matching-Probleme) gesucht. Eine Reihe weiterer Probleme (topologisches Sortieren, Zuordnungsprobleme wie
das Problem der stabilen Heirat, verschiedene Hüllen,..) erzeugen Graphen bzw. können in geeigneter Form
mit Graphen gelöst werden. Zu vielen der oben genannten Probleme sind verschiedene Algorithmen mit
unterschiedlichen Strategien bekannt; leider sind einige Probleme - vor allem mehrere Optimierungsprobleme - NP-hart
und lassen sich nur mit exponentieller Laufzeit lösen, sind also bei großen Graphen praktisch nicht
lösbar. Zum Glück gibt es oft schnelle durchaus brauchbare Näherungsverfahren, die z.B. in
Navigationssystemen (Routenplanern) eingesetzt werden. Dass exponentieller Aufwand rasch Jahrtausende langes Rechnen
oder Rechenzeiten viel länger als die Lebensdauer unseres Universums bedeuten kann, mag übrigens im
Zusammenhang mit Primzahltest auf meiner Mathematik-Hauptseite nachgelesen werden.
Mit dem kostenlosen und im Download nur 523 kB großen Programm Windisc von R. Parris (Stand Juli
2011; aus der auf meiner Mathematik-Seite schon in den Verweisen aufgeführten „Peanut"-Serie) können viele der oben genannten
Graphen-Probleme an kleinen Beispielen schrittweise nach verschiedenen Verfahren gelöst werden, sodass die
Funktion der Algorithmen im Ablauf bzw. in ihrer Arbeitsweise verfolgt werden können. Leider werden die
Algorithmen selbst nicht von Windisc oder in der Windisc-Hilfe angegeben.
Für die erst-genannten Wegsuchen-Probleme sollen im Folgenden Algorithmen in Java entwickelt werden.
zum Seitenanfang / zum Seitenende
Tiefensuche
Wie schon auf meiner Seite „Informatik mit Java", Teil e) bei den Suchen im Labyrinth ausgeführt, gibt es verschiedene Suchstrategien. Die Tiefensuche ist ein Verfahren, das ein systematisch experimentierender Mensch auch in der Realität ausführen könnte: Der Weg beginnt am Startknoten. Der Startknoten wird als 'besucht' markiert, damit man nicht später freiwillig wieder hier vorbei kommt und dabei eine unnütze Schleife gedreht hätte. Dann wird nach einer festen Regel ein bisher unbesuchter Nachbarknoten gesucht - beispielsweise wie hier, in dem man nacheinander alle Knoten beginnend vom Knoten mit der Nummer 0 in aufsteigender Reihenfolge überprüft, ob der gerade geprüfte Knoten von der augenblicklichen Position aus durch eine einzige Kante direkt erreichbar ist und bisher noch besucht wurde. Findet man einen solchen Nachbar, wird der Weg dorthin fortgesetzt und der so erreichte Nachbarknoten als 'besucht' markieret. Sofern dieser Nachbarknoten noch nicht das Ziel ist, wird er zum aktuellen Knoten erklärt und von hier aus wird wieder nach dem bereits beschriebenen Muster verfahren: Aus der Reihe der Knoten wird der nächste erreichbare, bisher unbesuchte Knoten gewählt, um vom aktuellen Knoten einen Schritt weiter dorthin zu gehen. Auch der neue Knoten ist damit besucht, wird zum aktuellen, usw. Der Weg endet mit Erreichen des Zielknotens. Gibt es von einem Knoten aber keinen unbesuchten Nachbarn mehr (weil man in einer Sackgasse gelandet ist), so setzt das Backtracking ein: man geht auf der letzten Kante um einen Knoten zurück (im gerichteten Digraph also gegen die Einbahnstraße!), d.h. man nimmt einfach den letzten Schritt zurück und tut so, als wäre man nie in der Sackgasse gewesen (hätte also auch nicht rückwärts raus gemusst), ohne allerdings die Besucht-Markierung des Sackgassen-Knotens zu löschen. Schließlich will man ja nicht wieder in dieser Sackgasse landen. Vom letzten Knoten vor der Sackgasse versucht man es einfach mit einem anderen Nachbarn. Sofern es keinen mehr gibt, wird das Backtracking fortgesetzt, d.h. man geht noch einen Knoten zurück, usw., bis man endlich wieder einen unbesuchten Nachbarn für einen neuen Wegversuch findet. Kommt man mit dem Backtracking bis zum Startknoten zurück und findet schließlich auch dort keine unbesuchten Nachbarn mehr, so ist klar, dass es keinen Weg zum Ziel gibt! Andernfalls hätte die Suche schon mit Erreichen des Ziels geendet.
Die Tiefensuche kann iterativ mit einem expliziten Keller (wie auf der Seite e)) oder rekursiv implementiert werden - im letzten Fall übernimmt der Laufzeitkeller (Stack) des Computers, auf dem die geöffneten rekursiven Methoden verwaltet werden, implizit die Kellerfunktion. Im nachfolgenden Quelltext sind beide Versionen dargestellt.
Wenn klar ist, nach welchem Schema systematisch die Nachbarn geprüft werden, kann man die Tiefensuche natürlich auch von Hand nachvollziehen und sich den Weg, den sie finden würde, schon vorab überlegen. Der gefundene Weg ist übrigens oft weder der kürzeste noch der günstigste - aber es ist ein Weg! Wenn es überhaupt Wege gibt, findet die Tiefensuche immerhin einen. (Andere Wege könnte man durch Änderungen in der Überprüfungsreihenfolge finden)
Suchklasse mit rekursiver Tiefensuche
| // Java-Graphen-Programm, für IFL13M -- Krell, 11/04 + 7.12.04 // www.r-krell.de public class Graf_mitSuche2 extends Graf_Matrix // oder extends Graf_Listen: //erbt normale Grapheneigenschaft und fügt Suchen hinzu { // -------------------------------------------------------------------------------------- boolean [] besucht; // für Tiefensuche: merkt sich, welche Knoten schon besucht wurden public String tiefensuche_rek (int start, int ziel) { int knZahl = holeKnotenzahl(); besucht = new boolean[knZahl]; // erzeugt besucht (global definiert für rekSuche) for (int i=0; i<knZahl; i++) // setzt für alle Knoten besucht auf false, weil.. { besucht[i] = false; // .. die Suche ja noch nicht los gegangen ist } String meldung = rekSuche (start, ziel, 0, ""); // Hier startet die (rekursive) Suche .. if (meldung.equals("")) // .. und gibt den Weg (oder bei Misserfolg nichts) zurück { meldung = "Kein Weg von "+start+" nach "+ziel+" gefunden!"; } return ("Tiefensuche: "+meldung+"\n"); } private String rekSuche (int knoten, int ziel, double kosten, String weg) { besucht [knoten] = true; // Jeder Knoten, der von der Suche betreten wird, // wird als besucht markiert if (knoten == ziel) // Ziel erreicht? { weg = "Weg gefunden (Gesamt="+kosten+"): "+ziel; } else // Ziel noch nicht erreicht? Dann zu einem unbesuchten Nachbarn { // ..gehen und von dort den Weg zum Ziel suchen: for (int nachbar = 0; nachbar < knotenzahl && !weg.startsWith("Weg gefunden"); nachbar++) { // Fürs Backtracking nach und nach alle Nachbarn prüfen! if ((!besucht[nachbar]) && (holeKantenKosten (knoten, nachbar) < Double.POSITIVE_INFINITY)) { weg = rekSuche (nachbar, ziel, kosten+holeKantenKosten(knoten,nachbar), weg); } } if (weg.startsWith("Weg gefunden")) { weg = weg+"<-"+knoten; // Bei Rekursions-Rückweg nach Erfolg: Knoten zur } // Wegbeschreibung dazu. Sackgassen werden nicht notiert! } return (weg); } ... |
sowie mit iterativer Tiefensuche
| public String tiefensuche (int start, int ziel)
//r-krell.de
12.3.'05 { String weg = ""; // für die Wegbeschreibung (als Ergebnis) double kosten = 0; // für die Gesamtkosten des Wegs int kn1, kn2 = ziel; // für die Gesamtkostenberechnung boolean[] besucht = new boolean[knotenzahl]; // erzeugt 'besucht' for (int i=0; i<knotenzahl; i++) // und setzt für alle Knoten { // besucht auf false, weil die besucht[i] = false; // Suche ja noch nicht gestartet ist } besucht[start] = true; // Startknoten wird als erstes besucht Keller keller = new Keller(); // erzeugt neuen leeren Keller keller.rein (new Integer(start)); // Startknoten in den Keller while (!keller.istLeer() && !weg.startsWith("Weg gefunden")) { int knoten = ((Integer) keller.zeige()).intValue(); if (knoten == ziel) // schon am Ziel? { weg = "Weg gefunden: "+ziel; kn2 = ((Integer) keller.raus()).intValue(); // kn2 = ziel! } else // Ziel noch nicht erreicht? Dann vom letzten Graphenknoten { // .. zu einem neuen Nachbarn und von dort Weg suchen: int nachbar = 0; while (nachbar < knotenzahl && (besucht[nachbar] || holeKantenKosten (knoten, nachbar) == Double.POSITIVE_INFINITY)) { nachbar ++; // weiterblättern (zu unbesuchtem erreichbaren Nachbarn) } if (nachbar < knotenzahl) { besucht [nachbar] = true; keller.rein (new Integer(nachbar)); //Nachbar in den Keller } else { Object verschrotten = keller.raus(); //Sackgasse: Backtracking! } } // Ende else } // Ende äußere while-Schleife if (keller.istLeer()) { return ("Kein Weg gefunden!"); } else // Kellerinhalt = Weg { while (! keller.istLeer()) //Weg beschreiben und Gesamtkosten berechnen { kn1 = ((Integer) keller.raus()).intValue(); weg = weg + " <- "+ kn1; kosten = kosten + holeKantenKosten (kn1, kn2); // Richtung beachten! kn2 = kn1; } return (weg + " (Kosten="+kosten+")\n"); } } |
Als Ergänzung zur Tiefensuche in Java sei auf meine Seite „Informatik mit Prolog" verwiesen: In Prolog lassen sich Graph und Tiefensuche eingängiger formulieren!
zum Seitenanfang / zum Seitenende
Breitensuche
Auch dieses Suchverfahren wurde schon auf meiner Seite
„Informatik mit Java", Teil e), beim Labyrinth vorgestellt. Ein einzelner Autofahrer im Strassengewirr oder ein
Fußgänger in einem Labyrinth kann diese Suche aber nicht tatsächlich ausführen, weil er sich an
jeder Kreuzung oder Abzweigung teilen müsste: Ausgehend vom Startknoten bzw. von jedem erreichten aktuellen
Knoten werden jeweils alle bisher unbesuchten direkt erreichbaren Nachbarknoten quasi gleichzeitig betreten. Auf
jedem Knoten wird sich wieder geteilt usw. Erreicht dann irgendwann einer der wieder geteilten Arme das Ziel, so ist
der Weg gefunden. Man muss nur noch diesen Arm zum Start zurückverfolgen, um die Wegebeschreibung anzufertigen.
Man kann sich vorstellen, es würde am Start Wasser auf den Graphen gegossen, das sich nur längs der Kanten
ausbreiten kann und an jedem Knoten in alle erlaubten Richtungen fließt. Das Wasser fließt also in vielen
Kanten gleichzeitig. Gibt es einen Weg, so erreicht irgendwo das Wasser als erstes das Ziel und man verfolgt dessen
Weg zurück.
In Wirklichkeit arbeitet der Algorithmus natürlich verschiedene Möglichkeiten nacheinander ab: so werden an
jeder Kreuzung alle bisher unbesuchten Nachbarn hintereinander (z.B. in der Reihenfolge ihrer Nummern) in eine
Schlange gesteckt und in der Schlange wird quasi Gleichzeitiges verwaltet.
Tatsächlich funktioniert das mit der Schlange so: In eine neue, gerade leer angelegte Schlange wird zuerst nur der Startknoten gesteckt. Er wird dadurch als besucht markiert, indem man in einer Extra-Reihung als seinen Vorgänger nochmal den Startknoten selber einträgt - oder jedenfalls irgendwas anderes als den Defaultwert -1. Dann nimmt man den Startknoten (oder später auch den jeweils ältesten, ersten Knoten mit der Nummer i) aus der Schlange heraus und prüft - hier wieder beim Knoten mit der kleinsten Nummer beginnend - welcher der Knoten j dem zuletzt aus der Schlange genommenen Knoten benachbart, d.h. durch eine Kante erreichbar ist, und bisher nicht besucht wurde. Findet man dabei das Ziel, ist die Suche zu Ende und man muss nur noch die Wegbeschreibung erstellen. Andernfalls (wenn der Nachbar j nicht das Ziel ist) markiert man ihn als besucht, indem man den zuletzt aus der Schlange genommenen Knoten i als seinen Vorgänger einträgt. Der Nachbar j wird dann hinten in die Schlange rein getan. Ebenso wird mit allen weiteren bisher unbesuchten Nachbarn des zuletzt ausgeschlangten Knotens i verfahren. Gibt es keinen Nachbarn mehr, wird der nächste Knoten aus der Schlange geholt, mit i bezeichnet, und dessen Nachbarn werden ebenso überprüft und eingeschlangt. Ist irgendwann die Schlange leer, ohne dass das Ziel erreicht wurde, gibt es keinen Weg. Andernfalls war die Bearbeitung der Schlange schon abgebrochen worden und man konnte sich vom erreichten Ziel über die Reihung mit den Vorgängereinträgen schon zum Vorgänger, von dort zum Vorvorgänger des Ziels usw. zurückhangeln zum Start und dabei die Wegbeschreibung bzw. auch die Kostensumme erstellen.
hier also (in Ergänzung des bereits angefangenen Quelltexts Graph_mitSuche2) die Breitensuche
| ... public String breitensuche (int start, int ziel) // www.r-krell.de { String weg = ""; int[] vorgänger = new int[knotenzahl]; for (int i=0; i < knotenzahl; i++) { vorgänger[i] = -1; // bisher nicht besucht. } Graf_Schlange schlange = new Graf_Schlange(); schlange.rein (new Integer(start)); // weil hier die Schlange nicht auf int spezialisiert ist, // sondern allgemein Objekte aufnimmt, muss ein Wrapper-Objekt erschaffen werden vorgänger[start] = start; // irgendwas >= 0 als 'Besucht'-Markierung boolean gefunden = false; while (!schlange.istLeer() && !gefunden) { // Solange Schlange nicht leer und Ziel nicht gefunden int i = ((Integer)schlange.raus()).intValue(); // Graphknoten i aus Schlange raus for (int j=0; j<knotenzahl && !gefunden; j++) // und alle unbesuchten Nachbarn j von i ... { // .. in die Schlange rein if (j!=i && vorgänger[j]<0 && (holeKantenKosten(i,j)<Double.POSITIVE_INFINITY)) { vorgänger[j] = i; // Nachbar j (kommt gleich in Schlange) wurde von i aus besucht if (j==ziel) { gefunden = true; // Ziel gefunden! } schlange.rein (new Integer(j)); } } } if (schlange.istLeer()) { weg = "Breitensuche: Kein Weg von "+start+" nach "+ziel+" gefunden!\n" ; } else // Ziel erreicht { double gesamtkosten = 0; int j = ziel; // jetzt rückwärts vom ziel aus do // zu seinem vorgänger, von dort wieder zum { // vorgänger usw. weg = "->"+j+weg; // und Graphknoten in Wegbeschreibung aufnehmen gesamtkosten = gesamtkosten + holeKantenKosten(vorgänger[j], j); // Beachte Kantenrichtung! j = vorgänger[j]; } while (j != start); // bis start erreicht. weg = "Breitensuche: Weg gefunden (Gesamt="+gesamtkosten+"): "+start+weg+"\n"; } return (weg); // Weg-Beschreibung zurück } // ----------------------------------------------------------------------------------------------------- // evtl. später noch andere Suchverfahren } |
Die Tiefensuche liefert übrigens immer - sofern vorhanden - einen Weg vom Start zum Ziel über möglichst wenige Zwischenknoten. Gilt im Graphen die Dreiecksungleichung, so ist dies auch ein kostengünstiger bzw. kürzester Weg. Grundsätzlich lässt sich nicht sagen, welche der beiden Suchen (Breiten- oder Tiefensuche) schneller ist. Das hängt vom Graphen bzw. vom gesuchten Weg ab. In beiden Verfahren werden aber alle Knoten des Graphen jeweils nur höchstens einmal besucht, sodass der Gesamtaufwand proportional zur Knotenzahl und damit recht gering ist. Aber man findet eben höchstens per Zufall eine kostenoptimale Lösung, meist nur irgendeinen Weg (und oft durch beide Verfahren verschiedene Wege).
Weitere Suchverfahren (z.B. das Verfahren von Dijkstra) bzw. ein Applet zum Ausprobieren der vorgestellten Suchen sollen später noch auf dieser Seite folgen. Fürs Erste folgt aber ein Aufgabenblatt mit Fragen zur Wiederholung und Vertiefung.
zum Seitenanfang / zum Seitenende
Wiederholungsfragen und Aufgaben zu den Suchverfahren
Nachstehend ist ein Aufgabenblatt abgebildet, das auch als pdf-Datei angesehen (oder durch Rechtsklick und „Ziel speichern unter.." zur späteren Bearbeitung auf den eigenen Rechner herunter geladen) werden kann. Lösungen werden nicht mitgeliefert, sollten aber nach aufmerksamer Lektüre dieser Seite leicht fallen:
graphensuche-aufgabenblatt.pdf (63 kB)
Für Fragen zum Keller oder zur Schlange verweise ich auf meine Seite „Informatik mit Java", Teil e) - aus dem Menü am Anfang dieser Seite auswählbar!
zurück zur Informatik-Hauptseite
(Die anderen Java-Seiten werden entweder mit dem
Menü hier am Seitenanfang oder
am besten auch auf der Informatik-Hauptseite ausgewählt)
Mehr zu Graphen und Tiefensuche auch auf meiner Prolog-Seite