Willkommen/Übersicht  >  Informatik  >   Prolog-Seite

Informatik mit Prolog

Kurzer Abriss über den Einsatz von Prolog (Edinburgh-Standard)
als alternative Programmiersprache im SII-Unterricht

Diese Seite kann durchaus auch als Ergänzung zu meinen Seiten „Informatik mit Java" angesehen werden. Insbesondere gibt es Bezüge zu den Wegsuchen in Graphen auf der Seite „Informatik mit Java, Teil g)" und Bezüge zu den Kellern auf der Seite "Informatik mit Java, Teil e)". Tatsächlich empfiehlt der SII-Lehrplan neben der Arbeit mit imperativen, objektorientierten Programmierkonzepten (wie sie z.B. mit Java verwirklicht werden) auch die Einführung in ein alternatives Programmier-Paradigma. Das „Programmmieren mit Logik" mit Prolog ist eine solche sinnvolle und lohnenswerte Alternative.

Auf dieser Seite finden Sie:

• Prolog-Konzept
• 1. Familien-Stammbaum (mit Fakten, Fragen und Regeln und erstem rekursiven Prädikat)
• 2. Datenbank Zugfahrplan
• 3. Kombinations-Rätsel
• 4. Prolog-Listen und deren rekursive Bearbeitung (mit Anregung zum Thema Keller [Stack])
• 5. Wegsuche in Graphen bzw. für Rätsel und Spiele

sowie

• Literaturhinweise
• Verweise auf fremde Prolog-Seiten

Eine vollständige Übersicht aller meiner Java-Seiten gibt's auf der Informatik-Hauptseite!

zum Seitenanfang / zum Seitenende

Prolog-Konzept

Prolog ist nicht mit herkömmlichen Programmiersprachen zu vergleichen: Es gibt keine Zuweisungen, keine Kontrollstrukturen, keine verschiedenen Datentypen (mit Ausnahme der Prolog-Liste). Alles, was man kennt und normalerweise für nötig hält, gibt es nicht. Vielmehr wurde Prolog entwickelt, um Leuten das Erstellen von Expertensystemen zu ermöglichen, die nicht programmieren können und normale Programmiersprachen auch nicht erlernen wollen. Dem Computer sollen der normalen menschlichen Logik entsprechend Fakten und Regeln (Oberbegriff: Klauseln) mitgeteilt werden. Um eine Ausgabe zu erhalten, müssen geeignete Fragen an das System gestellt werden. Wie das System dabei zu einer richtigen Antwort kommt, muss -- so zumindest die Idee -- nicht die Sorge des Anwenders sein: schließlich hat er einen intelligenten Computer vor sich, der aufgrund der erworbenen/eingegebenen Wissenbasis selbstständig die richtige Lösung finden soll. Der Entwurf von Algorithmen oder Klassenhierarchien ist für Prolog also völlig unnötig!

zum Seitenanfang / zum Seitenende

1. Familien-Stammbaum

Fakten

In vielen Prolog-Büchern wird das Konzept mit einem Stammbaum illustriert. Angesichts vieler „Patchwork"-Familien heute vielleicht nicht mehr die Regel, aber noch vorstellbar: hier sind die Eltern von Kindern miteinander verheiratet und alle Ehepaare haben auch gemeinsame Kinder!

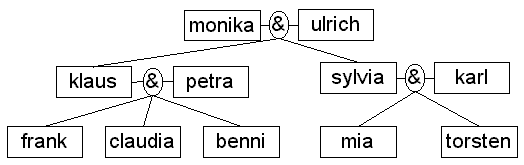
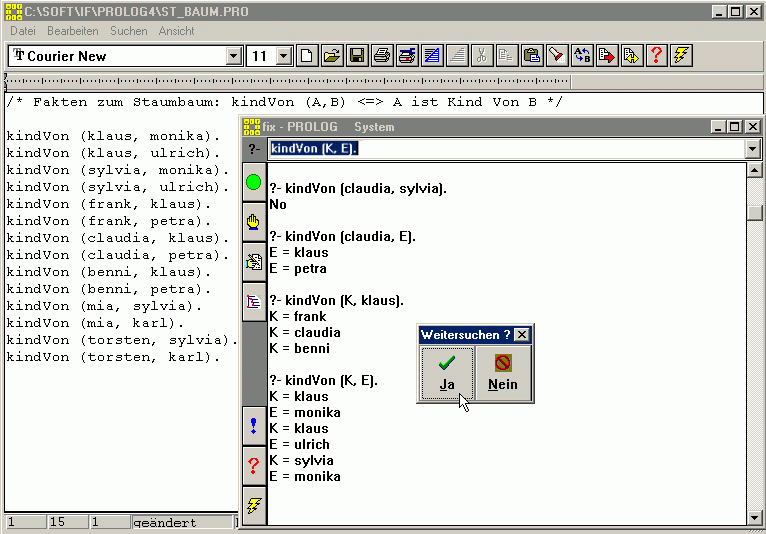
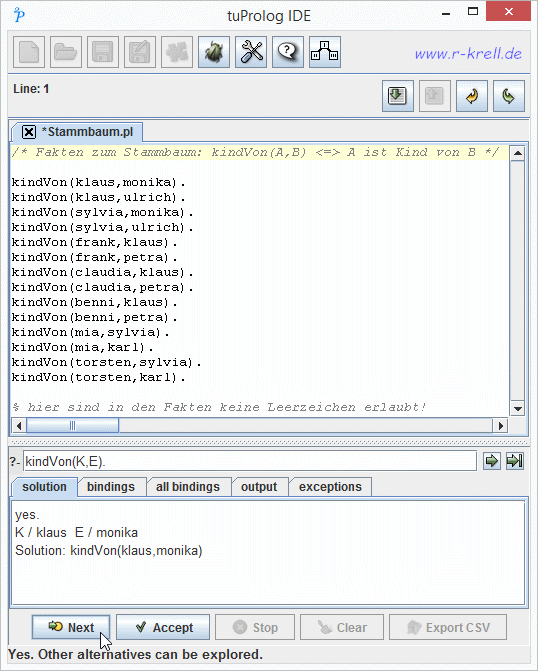
Fragen

Bei den Fragen gibt es verschiedene Möglichkeiten: Man kann ohne Variablen beispielsweise „?- kindVon (caudia, petra)." fragen und erhält als Antwort ein Yes, weil Prolog eine passende Klausel in seiner Datenbasis findet. Hingegen ist Claudia kein Kind von Sylvia -- jedenfalls findet Prolog nichts dergleichen und antwortet mit No. Enthält die Frage Variablen (die mit Großbuchstaben beginnen), so antwortet Prolog mit einer möglichen Variablenbelegung -- und gibt nach „Weitersuchen? Ja" -- auch noch jeweils eine weitere erlaubte Möglichkeit aus. So werden z.B. für E nacheinander beide Elternteile von Claudia gefunden (nochmal „Weitersuchen? Ja" hätte dann aber die Antwort No zur Folge, weil es keinen dritten Elternteil gibt) oder auch sämtliche Kinder von Klaus. Gibt es nur Variablen, gibt Prolog nacheinander alle zueinander passenden Kinder (K) und Elternteile (E) der Datenbasis aus. Die Reihenfolge von Klauseln in der Datenbasis ist zwar oft egal, wir merken aber, dass Prolog in genau dieser Reihenfolge nach Lösungen bzw. Antworten für gestellte Fragen sucht.

Regeln (und weitere Fragen)

Spannend ist die Erweiterung des Stammbaums um Regeln: Will man z.B. wissen, wer mit wem verheiratet ist, könnte man dem Computer das durch Fakten wie „verheiratet (monika, ulrich)." beibringen. Hier kann man aber auch ausnutzen, dass im Beispiel alle Paare Kinder haben, und zwei Personen P1 und P2 offenbar genau dann verheiratet sind, wenn sie (mindestens ein) gemeinsames Kind K haben:

Das Komma am Ende der zweiten Zeile wirkt als logische Und-Verknüpfung: die beiden letzten Zeilen müssen gleichzeitig erfüllt werden. Und weil in den beiden letzten Zeilen der gleiche Variablenname K vorkommt, muss es sich auch in beiden Fällen um das gleiche Kind handeln. Das ist wichtig, weil nur mit solchen gleichen Variablennamen Zusammenhänge hergestellt werden können. Das erinnert an die QBE-Fragetechnik bei Datenbanken (d.h. z.B. den 'query-by-example'-Abfragen in Paradox-Datenbanken), wo Verknüpfungen zwischen verschiedenen Tabellen über gleichnamige Variablen -- dort Beispielelemente genannt -- hergestellt wurden.

In ähnlicher Weise kann man Regeln für die Enkel-Großelternteil-Beziehung, für Geschwister und viele weitere Verwandtschaftsverhältnisse aufstellen: indem im Rumpf der Regel (nach dem „:-"-Zeichen) eine oder mehrere nach außen nicht sichtbare [d.h. im Kopf (vor dem „:-"-Zeichen) nicht verwendete und in der Antwort nicht ausgegebene] Variable mehrfach vorkommt/vorkommen.

Möchte man Elternteile nach Mutter und Vater unterscheiden, muss man dem System zumindest einmal alle Vertreter/Vertreterinnen eines Geschlechts durch Fakten mitteilen, d.h. z.B. „weibl (monika).  weibl (petra).  weibl (sylvia)." usw. aufführen. Das andere Geschlecht könnte dann per Regel aus allen Personen bestehen, die nicht weiblich sind, also

Achtung: Durch entsprechende Fragen stellt ma n schnell fest, dass jetzt nicht nur die oben aufgeführten Männer, sondern auch der dort unbekannte Hans-Peter („?- maennl (hanspeter)." => Yes), aber auch Uschi oder 783 angeblich männlich sind! Jedenfalls beantwortet Prolog z.B. die Frage „?- maennl (783)." mit einem klaren Yes, weil 783 eben nicht in der Datenbasis von weiblich steht, d.h. es kein Faktum der Form „weibl (783)." gibt! Bei der nachfolgenden Regel

stört das allerdings nicht, denn durch die „kindVon"-Klausel im Rumpf werden nur Personen für V ausprobiert, die in einer „kindVon"-Klausel an zweiter Stelle stehen (also auch im Stammbaum vorkommen). Man könnte sich also bequem alle Väter ausgeben lassen -- wenn die Kindernamen dabei gar nicht interessieren, fragt man mit der anonymen Variablen „_" und erhält auf „?- vaterVon (Papa, _)" mit Weitersuchen alle Namen von Vätern als mögliche Belegungen der Variablen Papa ausgegeben (zugehörige Lösungen für die anonyme Variable werden nicht gezeigt -- sie kann aber auch durch Mehrfachgebrauch innerhalb von Regeln oder Fragen keine Verbindung herstellen). Ohne Weiteres lassen sich übrigens durch die Frage „?- weibl (F)." alle eingegebenen Frauen nacheinander als Antworten erhalten, während die Frage „?- maennl (M)." den Computer ratlos lässt: Angesichts der unendlich vielen, für ihn unbekannten Gegenstände des Universums, die nicht als Namen in den paar weiblich-Regeln auftauchen, weiß Prolog nicht, was es alles für M einsetzten könnte oder soll und antwortet daher mit einem schlichten No.

Eine rekursive Regel (im Vorgriff auf Kommendes)

Wer will, kann übrigens auch den Stammbaum noch etwas erweitern und schon hier (statt erst in den Kapiteln 4 und 5, s.u.) ein rekursives Prädikat einführen. Angenommen, es gäbe außer den abgebildeten drei Generationen fünf oder mehr Generationen im Stammbaum, und man würde sich dafür interessieren, wer Nachfahre (Abkömmling) von wem ist. Eine naheliegende und durchaus richtige, wenn auch etwas umständliche Lösung wäre:

Vorstehend muss man für jede weitere Generation eine zusätzliche Regel angeben. Der Gedanke, z.B. bei der dritten Nachfahren-Regel (für Urenkel) eine Zeile Schreibarbeit zu sparen, indem man statt 2 mal „kindVon" einmal die Nachfahren-Regel für Enkel benutzt, könnte weiter gedacht werden: Schon bei der Nachfahren-Regel für Enkel könnte man statt einer Kind-Regel „kindVon (Zwischen, Alt)" die erste Nachfahren-Regel benutzen, die ja die Kind-Beziehung beinhaltet:

Damit werden aber alle weiteren Regeln überflüssig. Denn im rekursiven Aufruf in der letzten Zeile kann nicht nur die erste Nachfahren-Regel verwendet werden: Prolog setzt in die letzte Zeile auch die zweite Nachfahren-Regel selbst ein (die ja genauso heißt), so dass der rekursive Aufruf auch Enkelkinder beinhalten kann (und somit die zweite Regel insgesamt Urenkel liefert). Kann die zweite Regel aber Urenkel liefern und wird in der letzten Zeile verwendet, so kann die zweite Regel als Ganzes auch Ururenkel beschreiben. Und wenn die zweite Regel Ururenkel erzeugt und wieder in die letzte Zeile eingesetzt werden kann, dann... usw.: Die Rekursion kann also, ausgehend von einem einfachen Start (der ersten Nachfahren-Regel für die direkten Nachfahren, die Kinder) und einer zweiten, sich selbst aufrufenden Regel (rekursiver Aufruf in der letzten Zeile zusammen mit dem „kindVon"-Aufruf in der vorletzten Zeile, der immer eine Generation dazu fügt) beliebig viele Generationen überspannen, und ist daher universeller und auch noch schneller programmiert als die erste Lösung mit eigenen Regeln für jede neue Generation. Weitere Rekursionen begegnen uns unten in den Kapiteln 4 und 5 -- zunächst wird's aber wieder etwas anschaulicher:

zum Seitenanfang / zum Seitenende

2. Datenbank Zugfahrplan

Aufgaben „Prolog am Bahnhof":

• Es gibt eine Liste mit den Zugnummern und den Endstationen, z.B. fährt der ic721 nach Hamburg, der re4567 nach Essen, und der re457 nach Köln. Notiere geeignete Prolog-Fakten namens „endstation(..)." Achte dabei auf für Prolog richtige Groß-/Kleinschreibung.
• Die Züge haben planmäßige Abfahrtszeiten, z.B. fährt der ic721 um 8 Uhr 15 ab. Notiere auch hierfür einige Fakten „abfahrt (...)."
• Schließlich fährt jeder Zug von einem bestimmten Bahnsteig ab, z.B. fährt der ic721 vom Gleis 18 ab. Notiere einige Beispielfakten „gleis(..)."
• Oft möchte man wissen, wohin zum Beispiel der Zug vom Gleis 18 fährt. Notiere eine Regel, die z.B. auf die Frage „?- gleisZiel (18, Z)." mit Z=hamburg antwortet.
• Ähnlich wie in d) interessiert oft auch, wann der Zug zu einem bestimmten Ziel, z.B. nach Hamburg, abfährt. Schreibe eine Regel, die z.B. bei „?- zielZeit (hamburg, Std, Min)." mit Std=8 und Min=15 die Abfahrtszeit nennt.
• Im Fahrplan sind üblicherweise in einer Zeile hintereinander die Abfahrtszeit, die Zugnummer, der Zielbahnhof und das Abfahrtsgleis eingetragen. Schreibe eine Regel, die richtige Einträge produziert. Wie muss nach einem bestimmten Eintrag gefragt werden? Gibt es mehrere Fragemöglichkeiten? Erläutere ggf. mit zugehörigen Antworten! Gibt es auch Fragen, die mit Yes oder No beantwortet werden? Und wie müsste man fragen, um den gesamten Fahrplan ausgedruckt zu bekommen (wobei man nach jeder Zeile bzw. jedem Eintrag Weitersuchen? mit Ja beantworten muss)?

Lösungen zu den vorstehenden Aufgaben:

Hier wurde nochmal demonstriert, dass Verknüpfungen verschiedener Klauseln durch Variable geschehen. (In Kapitel 1 wurde schon die ähnliche QBE-Verknüpfung von Datenbanktabellen erwähnt.)

zum Seitenanfang / zum Seitenende

3. Kombinationsrätsel

Wie schon in den Kapiteln 1 und 2 gesehen, probiert Prolog automatisch oder nach „Weitersuchen? Ja" sämtliche Möglichkeiten durch, die die Datenbasis bereit stellt. Diese Eigenschaft kann benutzt werden, um Rätsel „durch Probieren" zu lösen. Zu beachten ist allerdings, dass man die Bedingungen möglichst früh anbringt (also ein Probieren nach der 'branch-&-bound'-Strategie durchführt) -- so hat es keinen Sinn, im nachfolgenden Rätsel auch noch die Autos zwei bis vier zu besetzen, wenn schon im ersten Auto eine falsche Person sitzt: Man kommt dadurch nicht mehr zu einer gültigen Gesamtlösung und vergeudet nur unnötig Speicherplatz und Rechenzeit. Die schlechtere 'brute-force'-Strategie würde jeweils erst eine vollständige Kombination aufstellen (d.h. hier alle vier Autos z.B. beim ersten Versuch alle mit Anette besetzten) und dann prüfen, ob diese Kombination zulässig ist.

Die Kinder Anette, Bernd, Claudia und Dieter fahren auf der Kirmes Auto-Scooter. Jedes Kind sitzt allein in einem eigenen Wagen. Die Autos sind rot, grün, gelb und blau. Anette sitzt nicht im roten Auto. Im grünen Auto sitzt ein Junge. Das Kind im blauen Auto ist die Schwester von Bernd. Dieter fährt im gelben Wagen. Schreibe ein Prolog-Programm, das auf die Frage
   ?- loese (Rot, Gruen, Gelb, Blau).
z.B. Rot = claudia, Gruen = bernd, Gelb = dieter und Blau = anette antwortet!

Durch die Aufgabenstellung wird schon ein Lösungs-Ansatz nahegelegt: Offenbar müssen Prolog die beteiligten Personen bekannt gegeben werden, damit das System dann für die (mit Großbuchstaben beginnenden) Variablen Rot, Gruen, Gelb und Blau diese Personen einsetzen kann, d.h. ausprobieren kann, ob z.B. Anette (bzw. in Prolog: anette) im roten Auto sitzen darf. Wenn/da dies laut Rätsel nicht erlaubt ist, brauchen die anderen Autos gar nicht erst besetzt werden, sondern das System soll für das rote Auto eine andere Person ausprobieren. Erst wenn hier ein erlaubter Insasse gefunden ist, wird -- gemäß der branch-&-bound-Strategie -- das grüne Auto besetzt, wobei die Person im roten Auto natürlich nicht noch gleichzeitig im grünen Auto sitzen kann. Ist auch das grüne Auto erlaubt besetzt, kann man das gelbe und schließlich das blaue Auto besetzen. Das folgende Prolog-Programm macht dies:

Prolog findet dann genau die oben schon angegebene Lösung. Auf „Weitersuchen? Ja" folgt No, d.h. es gibt keine weitere Lösung dieses Rätsels. Das „\="-Zeichen ist übrigens das Prolog-Ungleichheitszeichen; offenbar hat hier jede Programmiersprache ihre eigene Syntax („!=", „<>", ...).

zum Seitenanfang / zum Seitenende

4. Prolog-Listen und deren rekursive Bearbeitung

Bisher hatten wir nur mit einzelnen Variablen zu tun, die ohne jede Typddeklaration Konstanten wie anette oder hamburg oder auch (ganze) Zahlen (wie Gleisnummer, Stunden- oder Minutenzahl im Kapitel 2) aufnehmen konnten. Durch Aneinanderreihung mehrerer Variablen in einer Klausel (wie etwa bei eintrag im Kapitel 2, Aufgabe 6) konnte eine Art Klasse bzw. Objekt (oder ein Record für Pascal-Programmierer) nachgebildet werden. Wie beim Abriss über das Prolog-Konzept bereits angedeutet, lassen sich in Prolog aber auch beliebige Inhalte noch zu einer (Prolog-)Liste zusammenfassen.
Dies geschieht einfach dadurch, dass man die Elemente in eckige Klammern setzt. So sind [a, 4, 6+9, „hallo", du] oder [a1, b2] oder auch [ ] Beispiele für Listen, wobei [ ] die leere Liste darstellt. Natürlich können Listen auch wiederum Listen als Elemente enthalten, wie etwa die dreielementige Liste [ 2, [24, 7, [xyz], 1], plus], deren zweites Element selbst eine Liste ist (die ihrerseits als drittes Element eine einelementige Liste mit dem Inhalt xyz enthält).

Listentrenner „|"

Als einzige Möglichkeit, auf einzelne Elemente einer Liste zuzugreifen, gibt es in Prolog den Listentrenner „|", der eine Liste in ein (oder mehrere) Element(e) vor dem Trennstrich und in eine Liste mit dem Rest zerlegt. Das bedeutet, Elemente können immer nur vorne aus einer Liste heraus genommen werden. Will man ein hinteres Element isolieren, muss man zunächst alle vorangehenden Elemente mit dem Listentrenner entfernen, bis das gesuchte Element vorne in der Restliste steht und damit zugänglich ist. Da man die Prologprädikate in beliebiger Richtung benutzen kann, lassen sich umgekehrt einzelne Elemente mit dem Listentrenner auch vorne hinzufügen wie im nachfolgenden Prädikat test3 (vgl. auch Kapitel 1, wo kindVon zum Auffinden eines Kindes ebenso wie zum Feststellen des Vaters verwendet werden konnte, je nach dem, welcher der beiden „Parameter" eine Variable war). Hier also zunächst einige Übungen für den Gebrauch des Listentrenners:

Die verschiedenen Klauseln führen zu folgenden Ergebnissen:

• Die Frage ?- test1 (A, B). liefert die Antwort A = a und B = [4, 6+9, 'Hallo?', du]. Beachte: A ist ein einzelnes Element, B eine Liste („Restliste").
• Die Frage ?- test2 (X,Y,Z). liefert die Antwort X = a, Y = 4 und Z = [6+9, 'Hallo?', du]. Die ersten beiden Elemente der Beispielliste wurden abgetrennt, Z ist wieder eine Liste. Und natürlich können bei einer Frage die Variablen anders heißen, als in der Klausel -- hier z.B. Z statt Rest, nehmen aber entsprechend ihrer Stellung/der Reihenfolge in der Klammer bzw. in der „Parameter-Liste" die gleiche Rolle ein.
• Die Frage test3 (hoppla, N). liefert die Antwort N = [hoppla, a, 4, 6+9, 'Hallo?', du], hat also die Liste um das angegebene Element erweitert, d.h. das neue Element hoppla vorne in die Beispielliste rein geschrieben.. Die Regel hätte übrigens auch zu „test3 (Element, [Element | AlteListe]) :- beispiel (AlteListe)." verkürzt werden können.
  

Einige rekursive Listen-Prädikate

Wie gerade gesehen, ist der Zugriff aufs erste Element leicht (vgl. test1). Das letzte Element einer Liste kann hingegen nur rekursiv gewonnen werden. Es ist erreicht, wenn die Liste nur noch ein Element enthält, d.h. die Form [ LetztesElement ] hat. Hat die Liste hingegen mehr als ein Element, so müssen die vorderen sukzessive einzeln abgeschnitten werden. Da die abgeschnittenen Elemente nicht gebraucht werden, wäre auch eine anonyme Variable „_" dafür möglich. Das letzte Element jeder Liste ist natürlich das letzte Element der Restliste, wie man wieder an der gleichen Variablen L sieht. Würde man übrigens versuchen, das letzte Element einer leeren Liste zu ermitteln, erhält man als Antwort No: Die leere Liste kommt in den Klauseln letztesElement nicht vor!

In ähnlicher Weise können rekursiv die Elemente gezählt werden. Als einfachster Fall und damit gleichzeitig als Rekursionsende bietet sich das Zählen der Elemente einer leeren Liste an, die keine bzw. 0 Elemente enthält (Man könnte auch mit einer einelementigen Liste und der Anzahl 1 anfangen, erhält dann aber für die leere Liste die Anzahl No statt 0). Jede längere Liste enthält jeweils ein Element mehr als ihre Restliste, sodass durch Addition von 1 zur Mächtigkeit der Restliste die jeweilige Elementzahl erhalten wird. Auch hier muss das Rekursionsende vor der anderen gleichnamigen Regel stehen, weil Prolog die Datenbasis immer von oben abarbeitet und zuerst auf das Rekursionsende treffen muss, um nicht in eine Endlosrekursion zu verfallen. Und das Schlüsselwort „is" führt die Berechnung durch, weil in Prolog etwa „7 = 3 + 4" nicht gilt, weil links eine Zahl, aber rechts ein Term steht. „7 is 3+4" ist hingegen richtig, weil der Term rechts ausgewertet wird und dann sein Ergebnis 7 mit dem linken Ausdruck 7 verglichen wird. Apropos Rechnung: Es ist wichtig, verschiedene Variablen zu verwenden und sich nicht an die Zuweisung imperativer Sprachen anzulehnen, die „z = z + 1" erlauben -- ein solche oder auch die Aussage „Z is Z + 1" wäre in Prolog auf jeden Fall falsch, weil rechts vom Gleichheitszeichen 1 mehr steht als links, d.h. „=" oder „is" nie im mathematischen Sinne gelten kann. In Prolog wird aber logisch-mathematisch programmiert, und das Gleichheitszeichen wird nicht als Zuweisungszeichen wie in imperativen Sprachen missbraucht bzw. verwendet.

Im dritten nachfolgenden Beispiel geht es um die größte Zahl innerhalb einer Liste aus ganzen Zahlen. Einfach, direkt lösbar und damit als Rekursionsende geeignet ist wieder der Fall einer einelementigen Liste: die einzige Zahl ist gleichzeitig auch die größte. Bei längeren Listen muss das vordere Element abgeschnitten werden, um rekursiv zum einfachen Fall zu kommen. Jetzt ist aber nicht automatisch das Maximum der langen Liste gleich dem Maximum der Restliste: War das abgeschnittene Element größer als das Restmaximum, so ist statt dessen das abgeschnittene Element das Gesamtlistenmaximum. Entsprechend gibt's also zwei Regeln für das Abschneiden des ersten Elements!

Im vierten Prädikat soll überprüft werden, ob ein bestimmtes Element (mindesten einmal) in der Liste vorkommt. Taucht es irgendwann vorne (d.h. an der zugänglichen Stelle) in der Prolog-Liste auf, ist die Antwort Yes (egal, wie der Rest der Liste aussieht, für den daher hier die anonyme Variable eingesetzt werden konnte). Sonst kann man versuchen, rekursiv durch Abschneiden vorderer Elemente zu diesem sofort lösbaren Fall zu kommen. Möglicherweise gibt es aber irgendwann nichts mehr abzuschneiden, weil die Liste leer ist und man alle Elemente überprüft hat: Dann findet Prolog keine Regel „istElement" mehr, in der eine leere Liste vorkommt, und antwortet mit No.

Zum Schluss ein heiteres Beispiel: Eine Liste soll als lustig gelten, wenn sie mindestens dreimal die Konstante „ha" enthält. Es ist eine Klausel nötig, um die Lacher zu zählen. Und in einer weiteren Klausel wird entschieden, ob die Liste lustig ist. Dabei kann „mindestens 3" wahlweise mit „L > 2" oder mit „L >= 3" übersetzt werden. Gibt es weniger als drei Lacher, ist das Ergebnis No -- z.B. auf die Frage „?- heiterkeit ([a, 4, 6+9, 'Hallo?', du], Stimmung).", wo No erscheint (weil eben nicht Stimmung = lustig geantwortet werden kann).

Hier jetzt die beschriebenen Prädikate im Prolog-Text:

Dass durch den Listentrenner leicht das erste Element einer Liste abgetrennt werden kann, während die hinteren Elemente der Liste nur schwerer zugänglich sind, erinnert an den abstrakten Datentyp Keller (Stack), wie er auf meiner Java-Seite e) oder im Programmtext des Java-Applets zum Zentralabi 2014 beschrieben wird. Die im folgenden Bild gezeigten Kommentare sollen dazu anregen, den Keller in Prolog zu realisieren, sodass z.B. auch die gezeigte Frage zum gewünschten Erfolg führt:

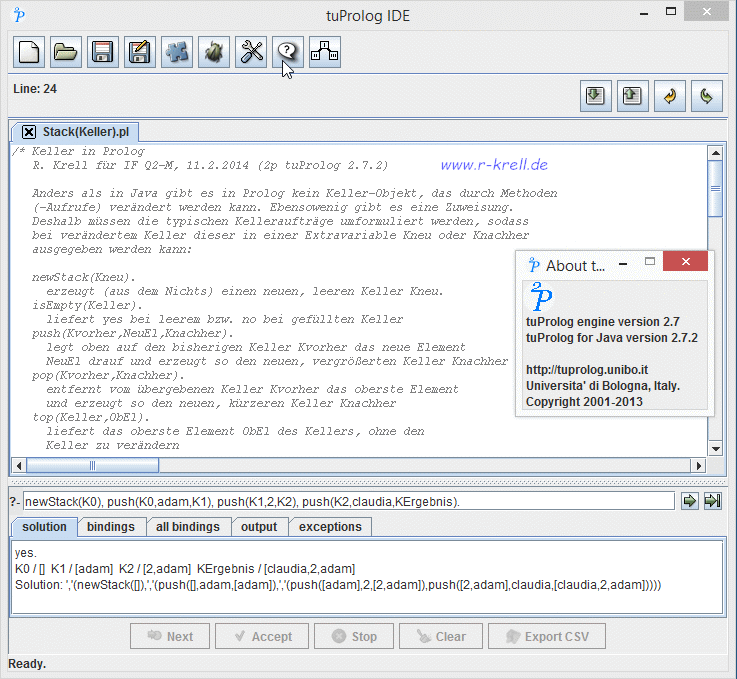
zum Seitenanfang / zum Seitenende

5. Wegsuche in Graphen und für Rätsel oder Spiele

Inzwischen wissen wir genug über Prolog, um damit die Wegsuche (und zwar die Tiefensuche) in einem Graphen realisieren zu können. Der Graph selbst kann durch die explizite Angabe aller Kanten mitgeteilt werden. So kann etwa der Graph, der auf meiner Seite „Informatik mit Java, Teil g) Graphen und Wegsuchen" als erstes abgebildet ist, unter Verzicht auf die Kantengewichte einfach wie folgt dargestellt werden -- Adjazenzmatrizen oder -listen sind nicht nötig!

Für die Wegsuche muss man bekanntlich (wie auf meinen Java-Seiten bei der Tiefensuche erläutert) eine Besuchtliste führen, um nicht in Zyklen zu geraten und Wegstücke mehrfach zu durchlaufen. Zunächst kommt nur der Startknoten in die Besuchtliste. Ist man mit nicht schon am Ziel, so betritt man vom gerade aktuellen Knoten den nächsten unbesuchten Nachbarn und sucht von dort nach dem gleichen Verfahren wieder den Weg zum Ziel (wobei jetzt auch der Nachbar besucht wurde, also der Einfachheit halber vorne an die Besuchtliste angefügt wird. Und „nach dem gleichen Verfahren" legt natürlich die Rekursion nahen!). Bei Sackgassen arbeitet Prolog automatisch mit Backtracking, d.h. hierfür ist kein Programmtext nötig. Erreicht man das Ziel, stehen daher in der Besuchtliste nur die Knoten des erfolgreichen Weges und man kann die Besuchtliste als Wegbeschreibung ausgeben. Da spätere Knoten vorne angefügt wurden, muss man die Knoten allerdings von hinten nach vorne lesen, um vom Start zum Ziel zu gelangen. Findet Prolog keinen Weg, so erhält man z.B. auf die Frage „?- wegsuche (0, 7)." vom Startknoten 0 zum in den Kanten nicht auftauchenden Knoten 7 die Antwort 0. Gibt es hingegen einen Weg, so kann man mit „Weitersuchen? Ja" auch noch andere Wege zwischen den gleichen Start- und Zielknoten ausgeben lassen. Die Wegsuche kommt sinnvollerweise in die gleiche Prologdatei, in der bereits die Kanten stehen, führt also die gerade angefangene Datei fort.

Wirklich vorteilhaft ist, dass die Kanten keineswegs wie im vorstehenden Beispiel explizit angegeben werden müssen. Dies eröffnet die Möglichkeit, leicht alle jene Rätsel und Spiele mit Prolog lösen zu können, wo man einzelne Züge macht -- sofern die Zugregeln als Regeln für Kanten formuliert werden können. Als Beispiel sei ein Nim(m)-Spiel gezeigt:

Anfangs liegen einige Streichhölzer auf dem Tisch. Die Spieler a und b müssen abwechselnd 1 bis 3 Hölzer nehmen. Verloren hat, wer das letzte Holz nehmen muss.

Liegen anfangs z.B. 11 Hölzer auf dem Tisch (H1 = 11) und Spieler a ist am Zug (Sp1=a), so könnte a drei Hölzer nehmen und damit die Hölzchenzahl auf H2 = 8 reduzieren, wobei dann Spieler Sp2 = b dran ist. Natürlich kann man nie mehr Hölzer nehmen, als da sind (H2 >= 0). Das führt zum abgebildeten Graphen und kann wie folgt in Prolog formuliert werden (wobei die Anfangszahl der Hölzchen im Programmtext noch völlig offen bleibt und erst bei der Frage gewählt werden braucht):

Bei „..." wird dann die ganz normale Wegsuche angeschlossen, wie sie einen Kasten früher angegeben wurde! Damit kann dann z.B. auf die Frage „?- wegsuche ([11,a], [1,V])." der Verlierer V gefunden und zuvor die passende Zugfolge ausgedruckt werden, die zu diesem Ergebnis führt. „Weitersuchen? Ja" liefert auch noch andere mögliche Spielverläufe (und mögliche andere Verlierer):

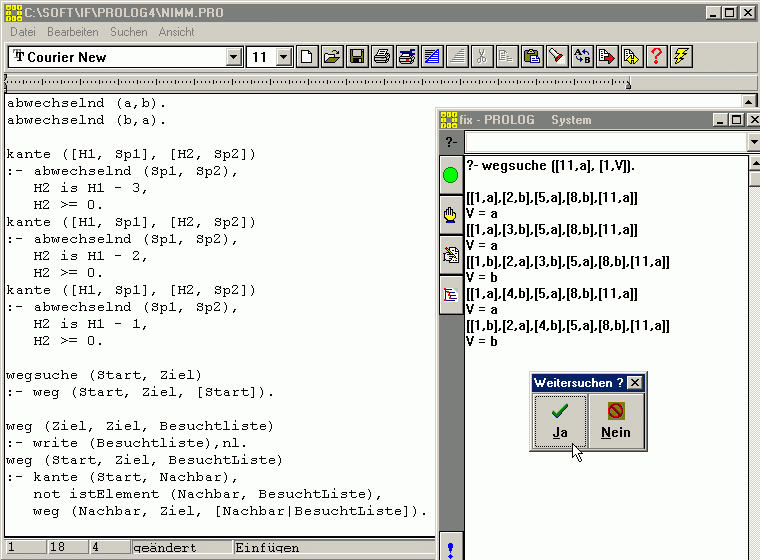
zum Seitenanfang / zum Seitenende

Literaturhinweise

Da ich mich selbst bereits vor längerer Zeit in Prolog eingearbeitet habe, bin ich bei der Literatur nicht unbedingt auf dem neuesten Stand. Trotzdem möchte ich einige (z.T. schon ältere, aber durchaus noch aktuelle und empfehlenswerte) Werke nennen:

• W.F. Clocksin / C.S. Mellish: Programmieren in Prolog. Berlin/Heidelberg (Springer) 1990, offenbar 2003 neu aufgelegt. Das ist wohl immer noch das Standardwerk für Prolog (und definiert letztlich den Edinburgh-Standard); obwohl nicht für den Schulgebrauch zugeschnitten, verständlich und gut lesbar.
• R. Yasdi: Logik und Programmieren in Logik. München/NewYork (Prentice-Hall) 1995. Ein Lehrbuch, hervorgegangen aus Uni-Vorlesungen.
• H. Göhner / B. Hafenbrak: Arbeitsbuch Prolog. Bonn (F. Dümmlers) 1991. Empfehlenswertes Werk für den Schulunterricht -- inzwischen offenbar auch als pdf-Datei im Internet (s.u., Verweise).
• R. Baumann: Datenbanken und Informationssysteme (= Arbeitshefte Informatik). Stuttgart (Klett) 1995. Hier führt Rüdeger Baumann in seiner gewohnten, teilweise etwas exemplarischen Art das Thema Datenbanken im Schulunterricht ausschließlich in Prolog ein (und verzichtet dabei völlig auf jegliche Datenbankprogramme wie etwa Access, Paradox, Informix, MySQL, o.ä.). (In alten LogIn-Artikeln hatte er sogar einmal vorgeschlagen, den gesamten Oberstufen-Informatik-Unterricht ausschließlich mit Prolog durchzuführen).
• G. Röhner: Informatik mit Prolog. Wiesbaden (Hess. Landesinstitut für Pädagogik) 3. Auflage 2007. In diesem neueren Buch (mit CD) werden zahlreiche Themen für den SII-Schulunterricht mit (SWI-)Prolog eingängig und mit Beispielen gut aufgearbeitet. Inhaltsverzeichnis und Bestellmöglichkeit für's Buch folgen unten, Verweis „Informatik mit Prolog". (G. Röhner ist auch der Autor des kostenlosen Editors für SWI-Prolog [s.u.] sowie des auf meiner Seite „Informatik mit Java, Teil a)" empfohlenen Java-Editors)

zum Seitenanfang / zum Seitenende

Verweise

Bevor Sie einen der folgenden Verweise (zuletzt aktualisiert im Februar 2014) anklicken, sollten Sie erst meine Seite zu Ihren Favoriten hinzufügen (Internet Explorer) oder ein Lesezeichen setzen (Firefox, Chrome, Opera,...), damit Sie anschließend sicher hierher zurück finden! Natürlich kann ich für den Inhalt fremder Seiten keine Verantwortung übernehmen. Wenn ein Verweis nicht funktioniert, dort inzwischen andere Inhalte zu sehen sind oder wenn Sie mir weitere gute Seiten empfehlen können, bitte ich um eine kurze Nachricht!

Hinweis: die fremden Seiten werden in einem neuen Browser-Fenster geöffnet. Geschieht beim Anklicken eines Verweises scheinbar nichts, wird das neue Fenster vermutlich vom aktuellen Fenster verdeckt -- bitte per Task-Leiste ins neue Fenster wechseln!

Ihnen gefällt meine Prolog-Seite bzw. mein Web-Angebot? Sie wollen auch andere auf diese Seite aufmerksam machen? Mit dem Verweis „per e-Mail weiter empfehlen" ganz unten auf dieser Seite können Sie eine e-Mail mit der URL versenden!

zurück zur Informatik-Hauptseite

zum Anfang dieser Seite

Willkommen/Übersicht  -  Was ist neu?  -  Software  -  Mathematik  -  Physik  -  Informatik  -   Schule: Lessing-Gymnasium und -Berufskolleg  -  Fotovoltaik  -  & mehr  -  Kontakt: e-Mail,  News-Abo, Gästebuch, Impressum  -  Grußkarten, site map, Download und Suche

Diese Seite ist Teil des Webangebots http://www.r-krell.de. Sie können diese Seite per e-Mail weiter empfehlen (tell a friend).