| www.r-krell.de |
| Webangebot für Schule und Unterricht,
Software, Fotovoltaik und mehr |
Willkommen/Übersicht > Mathematik >
Rezension von Mathematik-Software, Teil d)
:
Dynamische Geometrie-Software
(DGS)
Auf diesen Seiten berichte ich über meine Erfahrungen mit bzw. über persönliche Eindrücke von
verschiedenen Mathematik-Programmen, nämlich:
a) numerische Programme: Rechen- und
Zeichenhilfen
b) interaktive Programme: Lern- und Nachhilfe-Programme: b1) für die
Sekundarstufe I (SI) b2) für die Sekundarstufe II (SII)
c) Computer-Algebra-Systeme (CAS): genaues und symbolisches Rechnen, Termumformungen und
Zeichnen
e) Software zur Linearen Algebra und zur
Vektorgeometrie
zum
Seitenanfang / zum Seitenende
Rezension von Mathematik-Software
d) Dynamische Geometrie-Software (DGS):
geometrisches Konstruieren, Abbilden, Bewegen und Messen
Dem Vernehmen nach hat ursprünglich das Programm Cabri
Géometrè den dynamischen Geometrie-Systemen zum Siegeszug verholfen. Inzwischen haben andere
Programme nachgelegt, das Vorbild offenbar eingeholt oder gar überflügelt und verfügen über z.T.
erstaunliche Fähigkeiten. Im Unterricht sollen sie das Einüben in den Gebrauch von Zirkel und Geodreieck
nicht ersetzen, aber ergänzen: Die Stärken der Software liegen in der Dynamik: eine einmal erstellte
Zeichnung bleibt nicht statisch, sondern es kann an einzelnen Punkten gezogen und die Konstruktion nachträglich
verschoben und verzerrt werden. Wenn sich dabei trotzdem weiterhin z.B. die Höhen, Mittelsenkrechten oder
Winkelhalbierenden eines Dreiecks in jeweils einem Punkt schneiden, kann dies als Gesetzmäßigkeit erkannt
werden, die sonst nur aus vielen, vielen Einzelzeichnungen vermutet werden könnte -- sofern die Konstruktionen
von Hand auch alle mit der nötigen Präzision ausgeführt würden. Die vorgestellten Programme sind
preisgünstig bzw. sogar kostenlos. Getestet wurden aktuelle Versionen im Juli 2005.
zum
Seitenanfang / zum Seitenende
Die Aufgaben
Vorab habe ich vier Aufgaben ausgewählt, die neben den allgemeinen dynamischen
Konstruktionsmöglichkeiten jeweils verschiedene zusätzliche Fähigkeiten der Programme erfordern.
Anschließend sollten alle Aufgaben mit allen Programmen bearbeitet werden, um so festzustellen, wie weit
Lösungen möglich sind und wo bei diesem Vergleich Übereinstimmungen, Stärken oder Schwächen
der Programme erkennbar werden. Dass die Aufgaben eher den älteren Jahrgangsstufen entstammen (statt etwa der
Klasse 5/6), liegt an meiner größeren Unterrichteerfahrung mit höheren Klassen.
| 1. Thaleskreis: Steckt man in die (von Hand auf Pappe gezeichneten)
Endpunkte A und B einer Strecke Nadeln und schiebt vorsichtig das Geodreieck so dazwischen, das die beiden
Schenkel des rechten Winkels die Nadeln berühren, so kann man die Lage der „Spitze" des Geodreiecks
(=Scheitelpunkt C des rechten Winkels) auf der Pappe markieren. Dreht man das Geodreieck vorsichtig, lassen sich
weitere mögliche Lagen markieren, die -- wie sich schließlich herausstellt -- interessanterweise alle
auf einem (Halb-)Kreis liegen, dem so genannten Thaleskreis. Diese Kreis soll -- als Ortslinie des Scheitelpunkts
C -- auch mit den Programmen gefunden werden. Neben der Konstruktion des rechten Winkels muss die Spur eines
bewegten Punktes aufgezeichnet werden können. |
| 2. (Zweiter) Strahlensatz: Hier soll eine Strahlensatzfigur so gezeichnet
werden, dass sich der zentrale Winkel und die Lagen und Abstände der beiden Parallelen verändern
lassen. Vier Längen müssen gemessen und die Quotienten aus jeweils zwei Streckenlängen angezeigt
werden, damit beim dynamischen Bewegen auffallen kann, dass sich zwar alle Werte ändern können, die
beiden Quotienten aber jeweils gleiche Werte haben. Die Programme müssen also neben der Konstruktion auch
Längenmessungen und die Anzeige berechneter Zahlen ermöglichen. |
| 3. Tangente(n) vom Punkt P an einen Kreis: Diese (wie die nächste)
Aufgabe entstammt dem Bereich der Koordinatengeometrie, die seit wenigen Jahren in Nordrhein-Westfalen in der
Jahrgangsstufe 11 verbindlich ist. Gesucht ist die Funktionsvorschrift der Geraden t, die durch den Punkt P = (
xp | yp ) geht und den Kreis K: (x-d)2 + (y-e)2 = r2 [=
Kreis um M = ( d | e ) mit dem Radius r] in einem Punkt berührt. Weil man weiß, dass die Tangente
durch den Berührpunkt S orthogonal zum Radius (von M zu S) steht, kann S mit dem Thaleskreis über der
Strecke MP gefunden werden und dann die Steigung des Radius', daraus die der Steigung m der Tangente und
letztlich aus m und den Koordinaten des Punktes P die Tangentengleichung ermittelt werden. Während die
geometrische Konstruktion in allen Programmen möglich sein sollte, interessiert, ob auch Steigungen gefunden
bzw. berechnet und Geraden nach Funktionsvorschrift gezeichnet werden können. |
| 4. Parabeltest: Die eingescannte Bildvorlage einer Brücke oder hier
des Bogens über der Kölnarena soll in das Programm übernommen werden. Durch Wahl geeigneter
Zahlenwerte für die Parameter a und c soll dann eine (y-achsensymmetrische) Parabel p: y = a x2 +
c so über das Bild gelegt werden, dass ihr Graph genau dem abgebildeten Bogen folgt. Zeichnen einer Parabel
nach Vorschrift, einfache Variation der Parameter und das Einbinden eines Fotos sind hierzu erforderlich. |
Die vorstehenden Aufgaben wurden mit Euklid-DynaGeo,
GeoGebra sowie
mit Zirkel und Lineal in Angriff genommen. Zu meiner eigenen Überraschung konnte ich alle vier Aufgaben mit jedem der
drei Programme ohne große Umstände vollständig lösen. Natürlich gab es Unterschiede in der
Handhabung, die mal die eine, mal die andere Lösung etwas begünstigten oder leicht erschwerten. Mal konnte
mit der rechten, mal mit der linken Maustaste gezogen werden, oder Programm-Funktionen versteckten sich hinter
verschiedenen Icons der Werkzeugleiste oder in unterschiedlichen Menüs. Im Ergebnis waren die Unterschiede aber
tatsächlich geringer als erwartet und es gibt insgesamt keinen klaren Gewinner oder Verlierer: alle drei
Programme liegen recht dicht beieinander und können für diese Aufgaben ohne Weiteres empfohlen
werden!
Für alle drei Programme gibt's im Folgenden Bemerkungen zum Bearbeiten der
Aufgaben; mehr wird aus den Bildschirmfotos deutlich, wo -- soweit ohne Verdecken der Konstruktion möglich --
extra manche Menüs oder Dialogfenster zusätzlich aufgeklappt wurden, um nebenbei Bedienung oder
Besonderheiten der Programme anzudeuten. Achtung: alle Bildschirmfotos öffnen sich in neuen Fenstern
und sollten dort ggf. auf 100% vergrößert werden! Außerdem folgen nach der Einzelbesprechung
Hinweise zum Publizieren mit den Programmen sowie eine tabellarische Übersicht über Quellen und Preise
(alle Links auf fremde Seiten ohne Gewähr und Haftung).
zum
Seitenanfang / zum Seitenende
Euklid-DynaGeo 2.6e
Dieses ist von den drei besprochenen Programmen vermutlich das Bekannteste. Mehrere Verlage verkaufen CDs mit
fertigen Euklid-DynaGeo-Konstruktionen, bei deren Verwendung
im Unterricht Schülerinnen und Schüler verschiedener Jahrgangsstufen in die Geometrie eingeführt und
geometrische Sätze und Zusammenhänge erkennen sollen. Die Bedienung des Programms ist recht intuitiv und
übersichtlich. Allerdings ist es das einzige Programm, das für gezeichnete Geraden nicht irgendwo auch
einen Funktionsterm angibt.
 1. Thaleskreis (Aufgabenstellung s.o.): Das
Konstruktionsprinzip (das genau so auch mit den anderen beiden Programmen durchgeführt wurde) habe ich im Bild
erläutert (rechts auf die verkleinerte Version klicken: Bild öffnet sich in neuem Fenster und muss ggf.
noch vergrößert werden!); bei der Ortslinie gibt es zwei Möglichkeiten: Ist der Ziehpunkt wie im
Beispiel frei, so wird die Spur des Punktes C auf dem Bildschirm aufgezeichnet und bleibt auch dann noch in der
aufgezeichneten Form bestehen, wenn die Punkte A und B verschoben werden. Wird hingegen der Ziehpunkt z.B. an eine
Hilfsgerade (oder ein Zahlobjekt/Schieberegler) gebunden, dann ist die Ortslinie mit der Konstruktion verbunden und
die Linie wird bei Änderungen an die neue Strecke AB angepasst, so dass dann also immer ein ordentlicher
Halbkreis mitwandert. Im letzten Fall ist auch eine Animation möglich, d.h. ein automatisches Verschieben des
Ziehpunkts auf der Hilfslinie mit Aufzeichnung oder Nachfahren der Ortslinie.
1. Thaleskreis (Aufgabenstellung s.o.): Das
Konstruktionsprinzip (das genau so auch mit den anderen beiden Programmen durchgeführt wurde) habe ich im Bild
erläutert (rechts auf die verkleinerte Version klicken: Bild öffnet sich in neuem Fenster und muss ggf.
noch vergrößert werden!); bei der Ortslinie gibt es zwei Möglichkeiten: Ist der Ziehpunkt wie im
Beispiel frei, so wird die Spur des Punktes C auf dem Bildschirm aufgezeichnet und bleibt auch dann noch in der
aufgezeichneten Form bestehen, wenn die Punkte A und B verschoben werden. Wird hingegen der Ziehpunkt z.B. an eine
Hilfsgerade (oder ein Zahlobjekt/Schieberegler) gebunden, dann ist die Ortslinie mit der Konstruktion verbunden und
die Linie wird bei Änderungen an die neue Strecke AB angepasst, so dass dann also immer ein ordentlicher
Halbkreis mitwandert. Im letzten Fall ist auch eine Animation möglich, d.h. ein automatisches Verschieben des
Ziehpunkts auf der Hilfslinie mit Aufzeichnung oder Nachfahren der Ortslinie.
 2. Strahlensatz: Die Möglichkeit zur
Längen-Messung findet man unter dem Reiter „Messen & Rechnen" mit dem Icon „Abstand messen", in
dem man den Abstand der zweier per Mausklick ausgewählter Punkte misst und streckennah anzeigen lässt. Die
Beschreibung wie etwa „L(AC)=" steht in einer extra angelegten Textbox, die an die Strecke gebunden wurde. Die
in den Rahmen oben links angegebenen Quotienten wurden als so genannte Termobjekte (Taschenrechner-Icon)
eingefügt und werden bei Veränderung der Konstruktion automatisch aktualisiert. Dadurch ist die Gleichheit
leicht zu erkennen. Die im Beispiel zusätzlich angezeigte Konstruktionsbeschreibung wurde automatisch erstellt
und kann per Menü „Verschiedenes" > „Konstruktionstext zeigen.." abgerufen werden.
2. Strahlensatz: Die Möglichkeit zur
Längen-Messung findet man unter dem Reiter „Messen & Rechnen" mit dem Icon „Abstand messen", in
dem man den Abstand der zweier per Mausklick ausgewählter Punkte misst und streckennah anzeigen lässt. Die
Beschreibung wie etwa „L(AC)=" steht in einer extra angelegten Textbox, die an die Strecke gebunden wurde. Die
in den Rahmen oben links angegebenen Quotienten wurden als so genannte Termobjekte (Taschenrechner-Icon)
eingefügt und werden bei Veränderung der Konstruktion automatisch aktualisiert. Dadurch ist die Gleichheit
leicht zu erkennen. Die im Beispiel zusätzlich angezeigte Konstruktionsbeschreibung wurde automatisch erstellt
und kann per Menü „Verschiedenes" > „Konstruktionstext zeigen.." abgerufen werden.
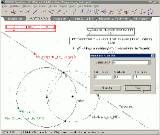 3. Tangente an einen Kreis: Es gibt kein Icon
oder Menübefehl für Tangenten, aber die Konstruktion mit dem Thaleskreis (Kreis durch P um den Mittelpunkt
Z zwischen M und P) gelingt problemlos. Eine Funktionsvorschrift für gezeichnete Geraden kann weder direkt
abgelesen noch umgekehrt zur Bestimmung eines Graphen eingegeben werden. Aber die Koordinaten eines Punktes P
können mit x(P) bzw. y(P) in Termobjekten abgefragt und in Rechnungen verwendet werden, sodass Steigungen ebenso
wie der Achsenabschnitt ermittelt und angezeigt werden können. Um schließlich zu „beweisen", dass
die Tangente genau die Gerade mit der berechneten (Orthogonalen-)Steigung und dem ermittelten y-Achsenabschnitt ist,
kann man einen Punkt durch Koordinatenangaben erzeugen, wobei die x-Koordinaten beispielweise die durch einen
Schieberegler (Reiter „Messen & Rechnen", Icon „Zahlobjekt erstellen") eingestellte Zahl iks ist,
während für die y-Koordinate des Punktes die Funktionsgleichung „y = a * iks + b" bzw. im Beispiel
(wegen der entsprechenden Bezeichnung in den Termobjekten rechts) „y = Orthogonalensteigung * iks + b"
angegeben wird. Ändert man nun iks (am Schieberegler) mit der Maus oder automatisch per Animation, so läuft
der Kontrollpunkt auf der geometrisch konstruierten Tangente entlang und zeigt so, dass die Tangente der [beim
(Kontroll-)Punkt] eingegeben Funktionsvorschrift genügt.
3. Tangente an einen Kreis: Es gibt kein Icon
oder Menübefehl für Tangenten, aber die Konstruktion mit dem Thaleskreis (Kreis durch P um den Mittelpunkt
Z zwischen M und P) gelingt problemlos. Eine Funktionsvorschrift für gezeichnete Geraden kann weder direkt
abgelesen noch umgekehrt zur Bestimmung eines Graphen eingegeben werden. Aber die Koordinaten eines Punktes P
können mit x(P) bzw. y(P) in Termobjekten abgefragt und in Rechnungen verwendet werden, sodass Steigungen ebenso
wie der Achsenabschnitt ermittelt und angezeigt werden können. Um schließlich zu „beweisen", dass
die Tangente genau die Gerade mit der berechneten (Orthogonalen-)Steigung und dem ermittelten y-Achsenabschnitt ist,
kann man einen Punkt durch Koordinatenangaben erzeugen, wobei die x-Koordinaten beispielweise die durch einen
Schieberegler (Reiter „Messen & Rechnen", Icon „Zahlobjekt erstellen") eingestellte Zahl iks ist,
während für die y-Koordinate des Punktes die Funktionsgleichung „y = a * iks + b" bzw. im Beispiel
(wegen der entsprechenden Bezeichnung in den Termobjekten rechts) „y = Orthogonalensteigung * iks + b"
angegeben wird. Ändert man nun iks (am Schieberegler) mit der Maus oder automatisch per Animation, so läuft
der Kontrollpunkt auf der geometrisch konstruierten Tangente entlang und zeigt so, dass die Tangente der [beim
(Kontroll-)Punkt] eingegeben Funktionsvorschrift genügt.
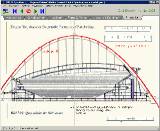 4. Parabelform der Kölnarena: In Euklid-DynaGeo kann immer nur höchstens ein Bild im .bmp-Format
eingelesen werden, das dann den Hintergrund unter dem Koordinatensystem bildet, wobei der Koordinatenursprung immer
genau in der Bildmitte ist. Das eingescannte Foto (hier aus dem Cornelsen-Schulbuch „Gymnasiale Oberstufe --
Mathematik -- 11. Schuljahr", Berlin 2000, ISBN 3-464-57210-2, Seite 74) musste also zuvor in einem
Bildbearbeitungsprogramm so in einen größeren Rahmen eingebettet und dann wieder passend beschnitten
werden, dass der als Ursprung ausgesuchte Punkt bezüglich der Bildhöhe wie der Bildbreite genau das
mittlere Bildpixel ist. Das Bild wird in Euklid-DynaGeo
immer in der Originalgröße angezeigt. Nach dieser etwas aufwändigen Vorarbeit gelang die Lösung
der Aufgabe mit dem Geometrie-Programm rasch: Zur Variation der beiden Parameter a und c wurden zusätzlich zum
Schieberegler iks (zum Durchspielen der x-Werte) jeweils Zahlobjekte erzeugt. Ein Punkt mit Koordinatenangabe wurde
durch x = iks und y = a * iks2 + c bestimmt und wandert (nach Einstellen von richtigem a und c) beim
Verändern von iks am Parabelbogen des Hintergrundbildes entlang. Erzeugt man die Spur bzw. Ortslinie dieses
Punktes, wird ein farbiger Parabelgraph sichtbar.
4. Parabelform der Kölnarena: In Euklid-DynaGeo kann immer nur höchstens ein Bild im .bmp-Format
eingelesen werden, das dann den Hintergrund unter dem Koordinatensystem bildet, wobei der Koordinatenursprung immer
genau in der Bildmitte ist. Das eingescannte Foto (hier aus dem Cornelsen-Schulbuch „Gymnasiale Oberstufe --
Mathematik -- 11. Schuljahr", Berlin 2000, ISBN 3-464-57210-2, Seite 74) musste also zuvor in einem
Bildbearbeitungsprogramm so in einen größeren Rahmen eingebettet und dann wieder passend beschnitten
werden, dass der als Ursprung ausgesuchte Punkt bezüglich der Bildhöhe wie der Bildbreite genau das
mittlere Bildpixel ist. Das Bild wird in Euklid-DynaGeo
immer in der Originalgröße angezeigt. Nach dieser etwas aufwändigen Vorarbeit gelang die Lösung
der Aufgabe mit dem Geometrie-Programm rasch: Zur Variation der beiden Parameter a und c wurden zusätzlich zum
Schieberegler iks (zum Durchspielen der x-Werte) jeweils Zahlobjekte erzeugt. Ein Punkt mit Koordinatenangabe wurde
durch x = iks und y = a * iks2 + c bestimmt und wandert (nach Einstellen von richtigem a und c) beim
Verändern von iks am Parabelbogen des Hintergrundbildes entlang. Erzeugt man die Spur bzw. Ortslinie dieses
Punktes, wird ein farbiger Parabelgraph sichtbar.
Insgesamt ist die Bedienung von Euklid-DynaGeo leicht zu
erlernen, bequem und logisch. Die Hilfe erwies sich als ordentlich; Such-Begriffe wie „Hintergrundbild"
führten schnell zu verständlichen Anleitungen. Schön sind die Schieberegler und Termobjekte und die
gut verwendbaren Textboxen (die auch einige Formatierungsmöglichkeiten erlauben und an Zeichnungsobjekte
gebunden werden können, um mit ihnen zu wandern). Bemerkenswert ist auch die bisher nicht erwähnte
Möglichkeit zur Rückblende / zum schrittweisen Nachvollziehen bereits erstellter Konstruktionen sowie die
Möglichkeit zur Ausgabe von Konstruktionsbeschreibungen. Etwas umständlich ist das Erzeugen von Graphen
durch bewegte Punkte mit Koordinatenangaben (wobei das Bewegen allerdings per Animation automatisiert werden kann).
Die analytische Funktionsvorschrift konstruierter Geraden kann nur über die Koordinaten geeigneter
zusätzlicher Punkte ermittelt werden. Weil das Koordinatensystem über dem Hintergrund-Bild nicht verschoben
werden kann, ist die vorherige entsprechende Vorbereitung des geplanten Hintergrundbildes nötig. [Nach Abschluss
der Besprechung teilte mir der Programmautor mit, dass in der im Herbst 2005 zu erwartenden Version 3.7 das
Hintergrundbild skalierbar und das Koordinatensystem darüber verschiebbar sein wird]. Euklid-DynaGeo verfügt über die einfachste Möglichkeit,
Arbeitsblätter ins Netz zu stellen, wie unten im Abschnitt „Publizieren.." noch
berichtet wird!
zum
Seitenanfang / zum Seitenende
GeoGebra 2.5.1
Dieses Programm hat auch einige CAS-Fähigkeiten und wurde diesbezüglich bereits bei meiner Rezension von Computer-Algebra-Systemen (Seite c)) besprochen. Hier interessieren jetzt die
geometrischen Fähigkeiten bei der Lösung der oben gestellten vier Aufgaben. GeoGebra will die Äquivalenz geometrischer und
analytisch/algebraische Beschreibung von Objekten durch gleichzeitige Darstellung von algebraischen
Objekteigenschaften und geometrischer Zeichnung in zwei parallelen Fenstern verdeutlichen. Das Erzeugen eines
Objekts, z.B. einer Geraden, ist im Allgemeinen auf jede der beiden Arten möglich (also durch Konstruktion oder
durch Eingabe eines Funktionsterms), wobei das Programm automatisch die jeweils andere Darstellungsform ergänzt.
Insofern sind gerade im Bereich der Koordinatengeometrie Vorteile zu erwarten, während jüngste
Schülerinnen und Schüler ohne Kenntnis des Koordinatensystems durch das (allerdings schließbare)
Algebra-Fenster vielleicht verwirrt werden. Aber der Reihe nach:
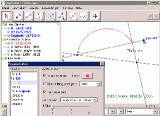 1. Thaleskreis: Die Konstruktion gelang einfach
und problemlos. Schön ist, dass die Punktnamen automatisch angezeigt werden (und mit der rechten Maustaste
leicht geändert werden können), ohne dass erst in umständlichen Dialogfenstern die Anzeige von Punkt-
oder Geradennamen ausgewählt werden muss. Im nach Rechtsklick auf den Scheitelpunkt des rechten Winkels (oder
seinen Eintrag im Objektbaum des Algebra-Fensters) erscheinenden Kontextmenü kann im Eigenschaften-Dialog leicht
das Erzeugen einer Spur angeklickt und so der Thaleskreis beim Verschieben des Zugpunktes erzeugt werden.
1. Thaleskreis: Die Konstruktion gelang einfach
und problemlos. Schön ist, dass die Punktnamen automatisch angezeigt werden (und mit der rechten Maustaste
leicht geändert werden können), ohne dass erst in umständlichen Dialogfenstern die Anzeige von Punkt-
oder Geradennamen ausgewählt werden muss. Im nach Rechtsklick auf den Scheitelpunkt des rechten Winkels (oder
seinen Eintrag im Objektbaum des Algebra-Fensters) erscheinenden Kontextmenü kann im Eigenschaften-Dialog leicht
das Erzeugen einer Spur angeklickt und so der Thaleskreis beim Verschieben des Zugpunktes erzeugt werden.
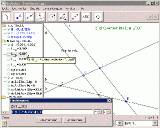 2. Strahlensatz: Die Streckenlängen
können wahlweise über das Icon „Abstand" (zu finden durch Klick auf den kleinen Pfeil rechts unten am
zunächst angezeigten Icon „Winkel" -- siehe Bild bei den nächsten Aufgabe) oder durch Eingabe des
Befehls „L_{AC} = Abstand[A,C]" in der Eingabezeile ermittelt werden; die Quotienten Q1 bzw. Q2 können nur
per Eingabezeile z.B. durch „Q1 = L_{AC}/L_{BD}" definiert werden und werden dann nur im linken Fenster
zahlenmäßig angezeigt. Die Werte ändern sich beim Ziehen an den freien Punkten; die
Übereinstimmung der beiden Quotienten wird augenfällig. Schön ist, dass GeoGebra die beweglichen Punkte (Freie Objekte) automatisch blau
färbt -- bei den anderen Programmen muss der Mensch für Färbung sorgen (wobei auch hier manuelle
Farbwahl möglich ist).
2. Strahlensatz: Die Streckenlängen
können wahlweise über das Icon „Abstand" (zu finden durch Klick auf den kleinen Pfeil rechts unten am
zunächst angezeigten Icon „Winkel" -- siehe Bild bei den nächsten Aufgabe) oder durch Eingabe des
Befehls „L_{AC} = Abstand[A,C]" in der Eingabezeile ermittelt werden; die Quotienten Q1 bzw. Q2 können nur
per Eingabezeile z.B. durch „Q1 = L_{AC}/L_{BD}" definiert werden und werden dann nur im linken Fenster
zahlenmäßig angezeigt. Die Werte ändern sich beim Ziehen an den freien Punkten; die
Übereinstimmung der beiden Quotienten wird augenfällig. Schön ist, dass GeoGebra die beweglichen Punkte (Freie Objekte) automatisch blau
färbt -- bei den anderen Programmen muss der Mensch für Färbung sorgen (wobei auch hier manuelle
Farbwahl möglich ist).
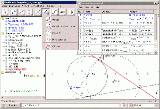 3. Tangenten: Als einziges der hier vorgestellten
Programme verfügt GeoGebra über die
Fähigkeit, direkt Tangenten zu erzeugen (die dann auch beide erstellt und angezeigt werden). Wegen des
Vergleichs mit den anderen Programmen wurde trotzdem auch die Thaleskreis-Konstruktion für S und T vorgenommen
(siehe automatisch erstelltes Konstruktionsprotokoll, Schritte 5 bis 8, statt S einfach als Schnittpunkt der Geraden
b mit dem Kreis K zu definieren). Die Steigung des Radius' MS kann entweder umständlich über die
Punktkoordinaten oder rascher über den Steigungs-Befehl erfolgen; im letzten Fall wird sogar ein Steigungsdreick
angezeigt. Gesuchte Größen wie die Steigung m und der y-Achsenabschnitt bt der Tangente können per
Eingabe entsprechender Formeln in der Eingabezeile erzeugt werden und werden links dann immer mit aktuellem
numerischen Wert angezeigt (die ursprüngliche Eingabe wird als Tooltip sichtbar, wenn man mit der Maus über
einem Objekt in der linken Liste verweilt). Die als „t: y = m * x + bt" eingegebene und rot gefärbte
Tangente liegt dann genau auf der konstruierten Geraden b, zeigt also die Richtigkeit der Funktionsvorschrift.
Natürlich hätte es hier auch gereicht, die ohnehin vom Programm sofort -- allerdings in der Allgemeinform A
x + B y = C -- angezeigte Funktionsvorschrift für die Gerade b von Hand in die Normalform umzuformen.
3. Tangenten: Als einziges der hier vorgestellten
Programme verfügt GeoGebra über die
Fähigkeit, direkt Tangenten zu erzeugen (die dann auch beide erstellt und angezeigt werden). Wegen des
Vergleichs mit den anderen Programmen wurde trotzdem auch die Thaleskreis-Konstruktion für S und T vorgenommen
(siehe automatisch erstelltes Konstruktionsprotokoll, Schritte 5 bis 8, statt S einfach als Schnittpunkt der Geraden
b mit dem Kreis K zu definieren). Die Steigung des Radius' MS kann entweder umständlich über die
Punktkoordinaten oder rascher über den Steigungs-Befehl erfolgen; im letzten Fall wird sogar ein Steigungsdreick
angezeigt. Gesuchte Größen wie die Steigung m und der y-Achsenabschnitt bt der Tangente können per
Eingabe entsprechender Formeln in der Eingabezeile erzeugt werden und werden links dann immer mit aktuellem
numerischen Wert angezeigt (die ursprüngliche Eingabe wird als Tooltip sichtbar, wenn man mit der Maus über
einem Objekt in der linken Liste verweilt). Die als „t: y = m * x + bt" eingegebene und rot gefärbte
Tangente liegt dann genau auf der konstruierten Geraden b, zeigt also die Richtigkeit der Funktionsvorschrift.
Natürlich hätte es hier auch gereicht, die ohnehin vom Programm sofort -- allerdings in der Allgemeinform A
x + B y = C -- angezeigte Funktionsvorschrift für die Gerade b von Hand in die Normalform umzuformen.
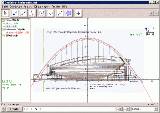 4. Parabelform der Kölnarena: In GeoGebra können beliebig viele Bilder (in einem der Formate .gif,
.jpg, .tif oder .png) eingebettet werden und durch Festlegen ihrer Eckpunkte im Koordinatensystem platziert bzw.
vergrößert / verkleinert, gestaucht und geschert werden. So ist es (notfalls mit etwas Probieren) für
jedes Bild möglich, es so zu setzen, dass jeder gewünschte Punkt über bzw. im Ursprung des
GeoGebra-Koordinatensystems zu liegen kommt. Im
Eigenschaften-Dialog wird ein Bild zum Hintergrundbild erklärt. Auch in GeoGebra gibt's Schieberegler zum Einstellen der Parameter a und c; nach
Eingabe des Funktionsterms „p: y = a * x^2 + b" wird automatisch der Parabelgraph angezeigt und kann durch
Betätigen der Schiebregler leicht dem gewünschten Verlauf angepasst werden.
4. Parabelform der Kölnarena: In GeoGebra können beliebig viele Bilder (in einem der Formate .gif,
.jpg, .tif oder .png) eingebettet werden und durch Festlegen ihrer Eckpunkte im Koordinatensystem platziert bzw.
vergrößert / verkleinert, gestaucht und geschert werden. So ist es (notfalls mit etwas Probieren) für
jedes Bild möglich, es so zu setzen, dass jeder gewünschte Punkt über bzw. im Ursprung des
GeoGebra-Koordinatensystems zu liegen kommt. Im
Eigenschaften-Dialog wird ein Bild zum Hintergrundbild erklärt. Auch in GeoGebra gibt's Schieberegler zum Einstellen der Parameter a und c; nach
Eingabe des Funktionsterms „p: y = a * x^2 + b" wird automatisch der Parabelgraph angezeigt und kann durch
Betätigen der Schiebregler leicht dem gewünschten Verlauf angepasst werden.
GeoGebra ist nach kurzer Eingewöhnung sehr angenehm
und schnell zu bedienen; durch die Parallelanzeige der Objekte im linken Fenster kann man (anders als in den
übrigen beiden Programmen) unabhängig von der Reihenfolge der Konstruktionsschritte leicht an jedes
beliebige Objekt heran, es ändern, umdefinieren oder einfach zusätzliche Informationen sammeln.
(Einzeiliger) Text kann durch Eingabe in Anführungsstrichen mittels der Eingabezeile eingefügt werden und
nach Anklicken des „Bewegen"-Icons (= Pfeil ganz links in der Werkzeugleiste) an jede beliebige Stelle des
Zeichenfensters geschoben werden. Oder auf Betätigen des ABC-Icons in der Werkzeugleiste öffnet sich ein
Dialogfenster für den Text. Wie bei den Objektnamen sorgen ein Unterstrich _ oder das Dach ^ für Tief- oder
Hochstellung des nachfolgenden Zeichens (oder aller in {..} eingeschlossenen folgenden Zeichen). Die Icons in der
Werkzeug-Leiste sind gruppiert; dass Ortslinie oder Schieberegler unter dem „Winkel"-Icon zu finden sind, merkt
man erst beim Suchen -- im Menü werden die Möglichkeiten nicht wiederholt. Dass die verschiebbaren freien
Objekte automatisch blau angezeigt werden, hatte ich ebenso wie die anpassbare Grafikeinbindung schon erwähnt.
Ein Konstruktionsprotokoll wird automatisch per Menübefehl erstellt. Für Zeichnungen besteht außerdem
die von CAD-Programmen bekannte Möglichkeit, Punkte im Koordinatengitter zu „fangen". Die durchdachten
Fähigkeiten bei klarer Struktur und -- sieht man von der anfänglichen Icon-Suche ab -- die letztlich
leichte und vor allem rasche Bedienung machen, insbesondere angesichts der Korrespondenz von Algebra und Geometrie in
den beiden Fenstern, dieses Programm zu meinem Favoriten unter den drei hier vorgestellten -- zumindest, so lange
keine Konstruktionsmöglichkeiten im Internet mit Werkzeugleiste angeboten werden sollen (s.u.): ein Feature, das
erst für kommende Versionen geplant ist.
zum
Seitenanfang / zum Seitenende
Z.u.L = Zirkel und Lineal 3.71
Dieses Programm hat schon eine längere Entwicklungsgeschichte vom einfachen Tool zum ausgereiften Programm
hinter sich und braucht sich mit seinen heutigen Fähigkeiten keinesfalls hinter anderen zu verstecken. Die Icons
sind alle gleichzeitig sichtbar, sodass das Blättern in den verschiedenen Reitern (wie bei Euklid-DynaGeo) oder die bei GeoGebra
gelegentlich nötige Suche in den ausklappbaren Gruppen entfallen. Außerdem stehen praktisch für alle
Befehle Hotkeys zur Verfügung, d.h. geübte Benutzerinnen oder Nutzer können die einzelnen Werkzeuge
auch per Tastendruck aktivieren, was eine noch schnellere Bedienung zulässt. Zu den einzelnen Aufgaben:
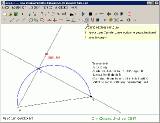 1. Thaleskreis: Die Konstruktion gelang ohne Weiteres.
Während Euklid-DynaGeo ohne Umschalttaste bei der Icon-Wahl nach
einmaligem Werkzeug-Gebrauch jeweils automatisch in den Zugmodus zurück springt, behält Zirkel und Lineal nach jedem Konstruktionsschritt das Werkzeug bei.
Bewegt werden kann trotzdem mit der rechten Maustaste. Mit der linken Maustaste erzeugt man gleichartige Objekte --
wer das nicht will, sollte ein neues Werkzeug wählen oder das Icon „Bewege Objekte" anklicken (bzw. Taste
'b' drücken). Beachtet man dies, gelingt die Konstruktion leicht und das Ergebnis kann sich sehen lasen; auch
mehrzeiliger Text ist gut einzugeben. Für das Aufzeichnen der Ortslinie stehen zwei Modi zur Verfügung:
wird der Zugpunkt von Hand bewegt, muss die erste (nicht automatisierte) Version per Icon „Ortslinie oder
Hüllkurve" oder Tastendruck 'o' gewählt werden.
1. Thaleskreis: Die Konstruktion gelang ohne Weiteres.
Während Euklid-DynaGeo ohne Umschalttaste bei der Icon-Wahl nach
einmaligem Werkzeug-Gebrauch jeweils automatisch in den Zugmodus zurück springt, behält Zirkel und Lineal nach jedem Konstruktionsschritt das Werkzeug bei.
Bewegt werden kann trotzdem mit der rechten Maustaste. Mit der linken Maustaste erzeugt man gleichartige Objekte --
wer das nicht will, sollte ein neues Werkzeug wählen oder das Icon „Bewege Objekte" anklicken (bzw. Taste
'b' drücken). Beachtet man dies, gelingt die Konstruktion leicht und das Ergebnis kann sich sehen lasen; auch
mehrzeiliger Text ist gut einzugeben. Für das Aufzeichnen der Ortslinie stehen zwei Modi zur Verfügung:
wird der Zugpunkt von Hand bewegt, muss die erste (nicht automatisierte) Version per Icon „Ortslinie oder
Hüllkurve" oder Tastendruck 'o' gewählt werden.
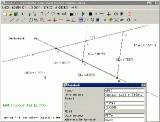 2. Strahlensatz: Die Konstruktion war nicht schwer. Um
die Namen der Punkte zu sehen, muss allerdings bei jedem Punkt im Eigenschaftsdialog (rechte Maustaste) der
'A'-Button gedrückt werden -- zumindest, solange man die Programm-Einstellungen nicht extra abändert. Bei
Strecken -- notfalls muss man zwei Punkte, die auf einer Geraden liegen, nochmal durch eine Strecke verbinden -- kann
man hier durch Anklicken des '0.5'-Buttons deren Länge sichtbar machen (beiGeraden, Strahlen oder Strecken ist
auch die Gleichung der Trägergeraden in der Form A*x+B*y = C im Eigenschaftsfenster zu sehen [siehe Bild zur
Tangente]: die Gleichung kann aber offenbar nicht auf dem Zeichenbildschirm sichtbar gemacht werden). Will man vor
die Streckenlänge etwas anderes als die Streckenbezeichnung schreiben, nimmt man auch für die
Längenangabe einen arithmetischen Ausdruck. Arithmetische Ausdrücke (Icon oder Taste 'x') werden auf jeden
Fall für die Berechnung der Quotienten gebraucht, wobei für das Verhältnis aus den Längen der
beiden Strecken namens s3 und s4 einfach „s3/s4" als Ausdruck und eine beliebige Beschreibung als wahlweise
davor anzuzeigender Text einzugeben ist. Die Anzeige kann an eine beliebige Stelle geschoben werden, so dass sie beim
Ändern an der Figur (mit „Bewege Objekte") gut im Blick ist, damit auch hier die Gleichheit beider
Quotienten auffällt.
2. Strahlensatz: Die Konstruktion war nicht schwer. Um
die Namen der Punkte zu sehen, muss allerdings bei jedem Punkt im Eigenschaftsdialog (rechte Maustaste) der
'A'-Button gedrückt werden -- zumindest, solange man die Programm-Einstellungen nicht extra abändert. Bei
Strecken -- notfalls muss man zwei Punkte, die auf einer Geraden liegen, nochmal durch eine Strecke verbinden -- kann
man hier durch Anklicken des '0.5'-Buttons deren Länge sichtbar machen (beiGeraden, Strahlen oder Strecken ist
auch die Gleichung der Trägergeraden in der Form A*x+B*y = C im Eigenschaftsfenster zu sehen [siehe Bild zur
Tangente]: die Gleichung kann aber offenbar nicht auf dem Zeichenbildschirm sichtbar gemacht werden). Will man vor
die Streckenlänge etwas anderes als die Streckenbezeichnung schreiben, nimmt man auch für die
Längenangabe einen arithmetischen Ausdruck. Arithmetische Ausdrücke (Icon oder Taste 'x') werden auf jeden
Fall für die Berechnung der Quotienten gebraucht, wobei für das Verhältnis aus den Längen der
beiden Strecken namens s3 und s4 einfach „s3/s4" als Ausdruck und eine beliebige Beschreibung als wahlweise
davor anzuzeigender Text einzugeben ist. Die Anzeige kann an eine beliebige Stelle geschoben werden, so dass sie beim
Ändern an der Figur (mit „Bewege Objekte") gut im Blick ist, damit auch hier die Gleichheit beider
Quotienten auffällt.
 3. Tangente: Die Konstruktion mit dem Thaleskreis war
in Zirkel und Lineal gut möglich, die Bestimmung und
Anzeige von Steigungen und y-Achsenabschnitt mit arithmetischen Ausdrücken z.B. der Form
„(y(S)-y(M))/(x(S)-x(M))" problemlos (über die Syntax der arithm. Ausdrücke informiert die Hilfe
gut). Das Einzeichnen eines Funktionsgraphen über die konstruierte Tangente geht zwar nicht per Icon in der
Werkzeugleiste, aber mit den Menübefehl „Bearbeiten" > „Funktion oder Kurve". Im erscheinenden
Dialogfenster kann als Variable x und als Ausdruck für den X-Wert ebenfalls x übernommen werden,
während als Ausdruck für den y-Wert hier „AD5*x+AD7" engegeben wird, weil AD5 und AD7 im Beispiel die
arithmetischen Ausdrücke zur Berechnung der Tangentensteigung und ihres y-Achsenabschnitts sind.
3. Tangente: Die Konstruktion mit dem Thaleskreis war
in Zirkel und Lineal gut möglich, die Bestimmung und
Anzeige von Steigungen und y-Achsenabschnitt mit arithmetischen Ausdrücken z.B. der Form
„(y(S)-y(M))/(x(S)-x(M))" problemlos (über die Syntax der arithm. Ausdrücke informiert die Hilfe
gut). Das Einzeichnen eines Funktionsgraphen über die konstruierte Tangente geht zwar nicht per Icon in der
Werkzeugleiste, aber mit den Menübefehl „Bearbeiten" > „Funktion oder Kurve". Im erscheinenden
Dialogfenster kann als Variable x und als Ausdruck für den X-Wert ebenfalls x übernommen werden,
während als Ausdruck für den y-Wert hier „AD5*x+AD7" engegeben wird, weil AD5 und AD7 im Beispiel die
arithmetischen Ausdrücke zur Berechnung der Tangentensteigung und ihres y-Achsenabschnitts sind.
 4. Parabelform der Kölnarena: Über den
Menüpunkt „Optionen" > „Hintergrund" > „Hintergrundbild laden.." lässt sich ein
.jpg- oder .gif-Bild laden, das jeweils die ganze gerade sichtbare Zeichenfläche einnimmt (und -- sofern
Zirkel und Lineal nicht im Vollbild, sondern im Fenster auf
dem Bildschirm ausgeführt wird -- durch Wahl einer geeigneten Fenstergröße
vergrößert/verkleinert bzw. gestaucht oder gestreckt werden kann). Das Z.u.L.-Koordinatensystem kann (mit etwas Geduld) an jede beliebige
Stelle verschoben werden, verschiebt sich aber bei nachträglichem Ändern der Fenstergröße wieder
relativ zum Bild. Schieberegler für das Ändern der Parameter per Maus stehen zwar nicht zur Verfügung
(könnten aber durch Verändern von Strecken ggf. selbst erzeugt werden), andererseits erlaubt der schon
erwähnte Menübefehl „Funktion oder Kurve" aber das leichte Eintippen eines Funktionsterms, sodass
hier durch Ausprobieren mit verschiedenen Zahlen bequem der richtige Funktionsterm getroffen werden kann.
Ärgerlicherweise wird beim normalen Speichern der Konstruktion (als .zir-Datei) das Hintergrundbild aber nicht
mit abgespeichert. Vielmehr musste es später nach dem Laden der Parabelkonstruktion erneut extra geladen werden.
[Nach Abschluss der Besprechung teilte mir der Autor von Z.u.L. mit, dass - durch diese Kritik angeregt - ab sofort (Version
3.81) beim erneuten Öffnen einer Zeichnung das Hintergrund-Bild aus dem gleichen Ordner automatisch mitgeladen
wird. Weitere Verbesserungen sollen in Kürze folgen.]
4. Parabelform der Kölnarena: Über den
Menüpunkt „Optionen" > „Hintergrund" > „Hintergrundbild laden.." lässt sich ein
.jpg- oder .gif-Bild laden, das jeweils die ganze gerade sichtbare Zeichenfläche einnimmt (und -- sofern
Zirkel und Lineal nicht im Vollbild, sondern im Fenster auf
dem Bildschirm ausgeführt wird -- durch Wahl einer geeigneten Fenstergröße
vergrößert/verkleinert bzw. gestaucht oder gestreckt werden kann). Das Z.u.L.-Koordinatensystem kann (mit etwas Geduld) an jede beliebige
Stelle verschoben werden, verschiebt sich aber bei nachträglichem Ändern der Fenstergröße wieder
relativ zum Bild. Schieberegler für das Ändern der Parameter per Maus stehen zwar nicht zur Verfügung
(könnten aber durch Verändern von Strecken ggf. selbst erzeugt werden), andererseits erlaubt der schon
erwähnte Menübefehl „Funktion oder Kurve" aber das leichte Eintippen eines Funktionsterms, sodass
hier durch Ausprobieren mit verschiedenen Zahlen bequem der richtige Funktionsterm getroffen werden kann.
Ärgerlicherweise wird beim normalen Speichern der Konstruktion (als .zir-Datei) das Hintergrundbild aber nicht
mit abgespeichert. Vielmehr musste es später nach dem Laden der Parabelkonstruktion erneut extra geladen werden.
[Nach Abschluss der Besprechung teilte mir der Autor von Z.u.L. mit, dass - durch diese Kritik angeregt - ab sofort (Version
3.81) beim erneuten Öffnen einer Zeichnung das Hintergrund-Bild aus dem gleichen Ordner automatisch mitgeladen
wird. Weitere Verbesserungen sollen in Kürze folgen.]
Zirkel und Lineal kann (z.B. wegen der Gleichungsanzeige
und der Darstellungsmöglichkeit von Funktionen und Kurven) mehr als Euklid-DynaGeo. Im Gegensatz zu beiden anderen Programmen sind auch Freihandlinien
('Malen') mit der Maus möglich. Ein Anfänger- und ein Schulmodus schränken die zur Auswahl stehenden
Werkzeuge ein; Aufgaben können als eine Art unveränderlicher Vorlagen zur Verfügung gestellt und
weiter bearbeitet werden. Dazu kommt die hier nicht getestete Möglichkeit, Makros zu definieren und zu
verwalten. Trotz des (nur in Version 3.7 noch auftretenden) Vergessens des Hintergrundbilds beim Speichern ist die
Grafikeinbindung zumindest leichter als bei Euklid-DynaGeo. Auch mehrzeiliger
Text kann (unformatiert) leicht eingebunden werden; Dateien lassen sich mit Kommentaren versehen (die beim Laden
angezeigt werden). Die insgesamt konsistente Bedienung erschien mir zwar anfangs etwas gewöhnungsbedürftig,
gelingt aber recht gut und ist außer mit der Maus sogar auch per Tastatur möglich.
Der Autor hat inzwischen Z.u.L. zum Open-Source-Projekt
gemacht, Schnittsellen und Formate veröffentlicht und lädt Programmiererinnen und Programmierer zur
Mitarbeit und Weiterentwicklung ein. Er hofft dadurch auch, dass sich das Z.u.L-Zeichnungsformat zu einem allgemeinen Standard entwickelt.
Inzwischen (Dezember 2007) bietet das Programm wohl die meisten und besten Möglichkeiten!
zum
Seitenanfang / zum Seitenende
Publizieren im Internet bzw. im Schulnetz
Alle drei Programme verfügen über die Möglichkeit, Konstruktionen ins Internet zu stellen bzw. zum
Öffnen in einem Webbrowser weiter zu geben. Und zwar können jeweils HTML-Seiten erzeugt werden, in die
Java-Applets mit den Zeichnungen eingebettet sind. Die Konstruktionen können dann auch im Schulnetz oder
Internet oder auf Rechnern, die die Geometrie-Software nicht enthalten, innerhalb der Webseite betrachtet und dort
dynamisch verändert werden.
Dabei nutzen die Programme unterschiedliche Ansätze: Zirkel und
Lineal sowie GeoGebra liefern jeweils eine
ca. 1 MB große .jar-Datei mit den benötigten Fähigkeiten mit, während Euklid-DynaGeo die Funktionalität bei bestehender
Internet-Verbindung vom DynaGeoX-Server lädt. Das enthebt Webmaster von der Pflicht, die .jar-Datei auf die
eigenen Seite hoch zu laden und vermindert den Traffic auf der eigenen Homepage. Zumindest auf Rechnern mit
installiertem Euklid-DynaGeo wird zum Glück bevorzugt
die lokale Installation benutzt und ist keine Internetverbindung nötig. (Tatsächlich bietet Euklid-DynaGeo zwei verschiedene HTML-Export-Möglichkeiten an: im
Geometria-Stil wird auch hier mit einer lokal kopierbaren jar-Datei -- mit 250 kB allerdings deutlich kleiner als bei
den Mitbewerbern -- gearbeitet). Soweit zumindest die Theorie.
Bei meinem Test funktionierten die Geometria-Variante von Euklid-DynaGeo und das Applet in der von GeoGebra erzeugten Webseite nicht sofort. Das GeoGebra-Applet verlangt auch beim Empfänger mindestens
installiertes Java 1.4.2 (mit installiertem Plug-in für den Webbrowser). Rüstet man den Browser
entsprechend auf, funktioniert die mit GeoGebra erzeugte
dynamische HTML-Seite einwandfrei: Die Punkte der Thaleskreis-Konstruktion konnten verschoben und beim Bewegen des
Zugpunktes der Thaleskreis schön aufgezeichnet werden. Beim Euklid-Geometria-Applet kam es hingegen beim Schieben des Punktes zu
einem Java-Fehler, Punktnamen und Ortslinie wurden nicht angezeigt.
Das Z.u.L-Applet und die aus Euklid-DynaGeo im DynaGeoX-Stil exportierte Webseite funktionierten auf
Anhieb einwandfrei (bei Zirkel und Lineal mussten zuvor
allerdings die Dateien zirkel.jar und die Konstruktion Thales.zir von Hand in den Ordner mit der Webseite kopiert
werden, während die anderen beiden Programme dies automatisch tun). Die letzte Variante hält noch eine
besondere Möglichkeit parat: Bei Euklid-DynaGeoX
braucht sich der Empfänger/Surfer nicht auf das Ziehen an den beweglichen Punkten der bereitgestellten Zeichnung
beschränken. Vielmehr kann die Autorin oder der Autor vor dem Export der Zeichnung durch Anklicken eine Reihe
von Werkzeugen auswählen (der Platz ist durch die gewählte Größe des Appletfensters
beschränkt), die der Webseitenbesucher bzw. die -besucherin benutzen kann, um selbst damit zu konstruieren.
Allerdings funktioniert das wegen dem auf ActiveX-Technik beruhenden DynaGeoX-Viewer nur auf Windows-Systemen und nur
mit dem Internet-Explorer. Das Beispiel zum Thales-Kreis findet sich hier (und verlangt ohne eigenes Euklid-DynaGeo auch eine gewisse Ladezeit):
Thales-Kreis zum Ausprobieren (nur mit MS Internet Explorer, als Euklid-DynaGeoX-Applet in
Extraseite)
Wenn innerhalb des Computerraums (oder bei allen Adressaten zu Hause) Internet Explorer und DynaGeo installiert
sind, ist es mit Euklid-DynaGeo also etwas bequemer oder
schneller, für Schülerinnen und Schüler Arbeitsblätter mit interaktiven Geometrie-Aufgaben zu
erzeugen. Bei heute üblichen schnellen Internet-Verbindungen ist dieser kleine Vorteil aber kaum noch
wichtig.
Lokal oder im Schulnetz (wo man ja keine langsamen Telefonmodem-Verbindungen befürchten muss) sind
natürlich die genannten größeren .jar-Dateien kein Problem. Und wer mit GeoGebra unter „Java 5" (SDK 1.5) konstruiert, erhält sogar
offenbar ein kleineres, nur noch ca. 400 kB großes .jar-Archiv. Wer den Traffic oder den Aufwand zur
Bereitstellung der .jar-Datei auf der eigenen Homepage fürchtet, kann seine GeoGebra-Zeichnungen außerdem kostenlos auf dem
GeoGebra-Wiki-Server veröffentlichen, muss dort offenbar nur die (sehr kompakten) .ggb-Zeichnungs- Dateien
hochladen und sich um den Rest nicht kümmern.
Schließlich wurde mir unmittelbar nach Abschluss der vorstehenden Besprechung mehrfach mitgeteilt, dass auch
Z.u.L. ebenfalls die von mir bei Euklid-DynGeo so gelobte Fähigkeit besitzt, Schülerinnen und
Schülern bzw. Websurfern auf der Webseite mit der Zeichnung auch eine Werkzeug-Leiste anzubieten, so dass nicht
nur Ziehen, sondern auch eigenes Konstruieren möglich ist -- und das bei Zirkel und Lineal sogar plattformunabhängig (aber bei langsamer
Internetverbindung eben leider mit langen Ladezeiten). Dies war mir wohl -- ebenso wie entsprechende wohl noch
bescheidene Ansätze für fortgeschrittene Benutzer in GeoGebra -- entgangen; ich will es aber demnächst noch ausprobieren
und werde ggf. entsprechende Erfahrungen nachtragen.
zum
Seitenanfang / zum Seitenende
Tabelle mit Bezugsquellen und Preisen der drei
Programme
| |
Euklid-DynaGeo |
GeoGebra |
Zirkel und Lineal |
| getestete Version |
2.6e |
2.5.1 |
3.71 |
Autor und
Webadresse |
Roland Mechling
http://www.dynageo.de |
Markus Hohenwarter
www.geogebra.at |
Rene Grothmann
www.z-u-l.de |
| Downloadgröße |
6,6 MB |
2,5 MB |
3,8 MB |
Preis (Stand Juli 2005)
- Einzellizenz
- Schullizenz |
Shareware (Gratis-Test, danach:)
29 €
87 € (inkl. Schüler 145 €) |
Freeware
kostenlos 0 €
kostenlos 0 € |
Freeware
kostenlos 0 €
kostenlos 0 € |
| Plattform |
Windows |
beliebig, sofern Java vorhanden *)
|
| aktuelle Version im Juli 2005 |
2.6e |
2.6a |
3.71 (ab 28.7.offenbar 3.81) |
| Nachtrag: aktuelle Version im Dezember 2007 |
3.0 f (2,6 MB) |
3.0.0 (22.7 MB) |
6.5 (6,3 MB) |
*) für GeoGebra mindestens Java 1.4.2 oder 1.5 -- Z.u.L. funktioniert auch mit der Java-VM, die mit dem
aktuellen Internet-Explorer mitgeliefert wird (möglichst aber 1.2 oder neuer).
zurück zur „Mathematik"-Hauptseite
 1. Thaleskreis (Aufgabenstellung s.o.): Das
Konstruktionsprinzip (das genau so auch mit den anderen beiden Programmen durchgeführt wurde) habe ich im Bild
erläutert (rechts auf die verkleinerte Version klicken: Bild öffnet sich in neuem Fenster und muss ggf.
noch vergrößert werden!); bei der Ortslinie gibt es zwei Möglichkeiten: Ist der Ziehpunkt wie im
Beispiel frei, so wird die Spur des Punktes C auf dem Bildschirm aufgezeichnet und bleibt auch dann noch in der
aufgezeichneten Form bestehen, wenn die Punkte A und B verschoben werden. Wird hingegen der Ziehpunkt z.B. an eine
Hilfsgerade (oder ein Zahlobjekt/Schieberegler) gebunden, dann ist die Ortslinie mit der Konstruktion verbunden und
die Linie wird bei Änderungen an die neue Strecke AB angepasst, so dass dann also immer ein ordentlicher
Halbkreis mitwandert. Im letzten Fall ist auch eine Animation möglich, d.h. ein automatisches Verschieben des
Ziehpunkts auf der Hilfslinie mit Aufzeichnung oder Nachfahren der Ortslinie.
1. Thaleskreis (Aufgabenstellung s.o.): Das
Konstruktionsprinzip (das genau so auch mit den anderen beiden Programmen durchgeführt wurde) habe ich im Bild
erläutert (rechts auf die verkleinerte Version klicken: Bild öffnet sich in neuem Fenster und muss ggf.
noch vergrößert werden!); bei der Ortslinie gibt es zwei Möglichkeiten: Ist der Ziehpunkt wie im
Beispiel frei, so wird die Spur des Punktes C auf dem Bildschirm aufgezeichnet und bleibt auch dann noch in der
aufgezeichneten Form bestehen, wenn die Punkte A und B verschoben werden. Wird hingegen der Ziehpunkt z.B. an eine
Hilfsgerade (oder ein Zahlobjekt/Schieberegler) gebunden, dann ist die Ortslinie mit der Konstruktion verbunden und
die Linie wird bei Änderungen an die neue Strecke AB angepasst, so dass dann also immer ein ordentlicher
Halbkreis mitwandert. Im letzten Fall ist auch eine Animation möglich, d.h. ein automatisches Verschieben des
Ziehpunkts auf der Hilfslinie mit Aufzeichnung oder Nachfahren der Ortslinie.









