| www.r-krell.de |
| Webangebot für Schule und Unterricht, Software, Fotovoltaik und mehr |
Willkommen/Übersicht > Mathematik >
Rezension von Mathematik-Software, Teil c) :
Symbolisch arbeitende Software (CAS=Computer-Algebra-Systeme)
Auf diesen Seiten berichte ich über meine Erfahrungen mit bzw. über persönliche Eindrücke von verschiedenen Mathematik-Programmen, nämlich:
a) numerische Programme: Rechen- und Zeichenhilfen
b) interaktive Programme: Lern- und Nachhilfe-Programme
| c) Computer-Algebra-Systeme (CAS): genaues und symbolisches Rechnen, Termumformungen und Zeichnen |
d) Dynamische Geometrie-Software (DGS): geometrisches Konstruieren, Abbilden, Bewegen und Messen
e) Software zur Linearen Algebra und zur Vektorgeometrie
zum Seitenanfang / zum Seitenende
Rezension von Mathematik-Software
c) Computer-Algebra-Systeme (CAS):
genaues und symbolisches Rechnen, Termumformungen und Zeichnen
Inzwischen sind auch Programme erschwinglich geworden, die formale Umformungen
mit Buchstaben beherrschen, also z.B. den Term der Stammfunktion mit Hilfe der Integrationsregeln algebraisch
ermitteln und exakte Rechnungen vornehmen können (CAS=Computer-Algebra-Systeme). Diese Programme sind nicht nur
weit leistungsfähiger als die in Teil a) vorgestellten, sondern erobern allmählich den Unterricht (vgl.
neuere Schulbücher und diverse Unterrichtsmaterialien von Schulbuchverlagen oder etwa dem Stark-Verlag sowie
verschiedene Webangebote). Getestet wurde im Mai 2005.
GeoGebra wird auch auf der Seite d) meiner Software-Rezensionen als dynamisches Geometrie-Programm vorgestellt. Und
auf Literatur über die Eignung von MuPAD und Derive für die Lineare Algebra und die Vektorgeometrie wird
auf der Seite e) meiner Mathe-Software-Besprechungen hingewiesen.
zum Seitenanfang / zum Seitenende
Die Aufgabe
Im Folgenden sollen drei Programme verglichen werden. Um Übereinstimmungen und Unterschiede deutlicher zu machen, wurde mit jeder Software die gleiche Aufgabe bearbeitet
| - und zwar soll der Flächeninhalt zwischen der x-Achse und dem Graphen der auf meiner Seite „Einführung in die Integralrechnung mit Fotovoltaik, einer Wiese und Excel" vorgestellten Funktion f(x) = 1/4 x2 + 2 im Bereich von 0 bis 4 bestimmt werden. Die Fläche soll gezeichnet und mit Unter- und Obersumme approximiert werden; außerdem soll der genaue Integralwert berechnet werden. |
Diese Aufgabe wird im Folgenden mit Derive, MuPAD und GeoGebra gelöst; anschließend folgen eine tabellarische Übersicht und Hinweise auf weitere Programme und fremde Webseiten (alle Links ohne Gewähr bzw. Haftung).
Auch wenn ich diese Aufgabe zum Test benutzt habe, glaube ich trotzdem, dass zumindest bei der Einführung in
die Integralrechnung zunächst auf CAS-Software verzichtet werden sollte, bis die Schülerinnen und
Schüler eine sichere Vorstellung von der Integration entwickelt haben. Ein zumindestens in Ansätzen
handlungsorientierter Zugang wie auf meiner vorgenannten Webseite „Einführung in die Integralrechnung..",
der zudem nicht auf ein Medium festgelegt ist, erscheint mir sinnvoller.
Hier ermöglicht nur GeoGebra mit seinem Schieberegler eine geringfügige Interaktion, ansonsten produziert
der Computer die Ergebnisse. Bei MuPAD mag der Zwang zu erklärenden (Zwischen-)Texten noch das Nachdenken bzw.
das Verständnis fördern.
Ansonsten dürfte der sinnvolle Einsatz aller Programme eher da liegen, wo nach erfolgter Einführung der
Integralrechnung durch Betrachtung einer Reihe zusätzlicher Beispiele neue Regeln oder Zusammenhänge
gefunden werden sollen, wo realitätsnahe Anwendungen im Vordergrund stehen und der (bei realistischen Zahlen oft
lästige und von Hand sehr langwierige oder kaum noch zu leistende) Rechenaufwand an den Computer delegiert
werden soll, oder wo Lehrkräfte zur Vorbereitung bzw. Schülerinnen und Schüler nachträglich zur
Kontrolle rasch die richtige Lösung von (Haus-)Aufgaben erhalten wollen. Insbesondere MuPAD eignet sich auch gut
zum Anfertigen von Facharbeiten oder mathematischen Aufsätzen und Artikeln.
zum Seitenanfang / zum Seitenende
Lösung mit Derive
Das bekannteste, traditionsreichste und bisher wohl noch am weitesten verbreite CAS-Programm ist Derive, das Texas Instruments in einer angepassten Version auch auf Taschenrechnern implementiert hat. Hier wird die (seit Mitte 2007 nicht mehr erhältliche!) PC-Version besprochen.

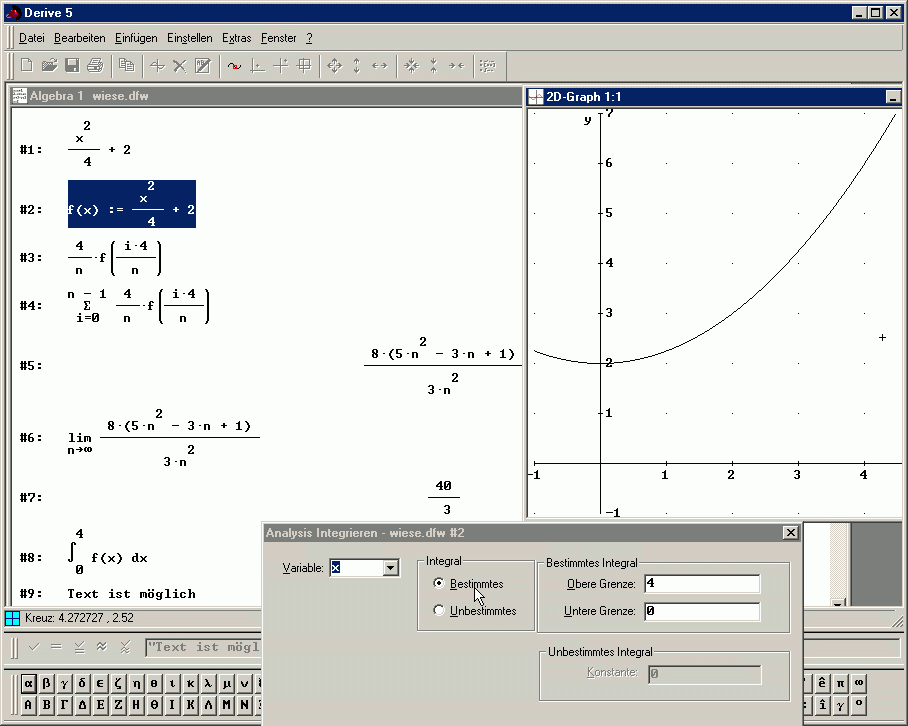
Das Programm arbeitet mit einer klar strukturierten Oberfläche. Die Eingabe erfolgt in einer besonderen Eingabezeile (standardmäßig am unteren Bildschirmrand, im Bild gerade mit "Text ist mögl[ich"] gefüllt). Dort kann die Funktionsvorschrift etwa als „f(x) := x^4/4+2" eingegeben werden. Im großen Rechen- bzw. Protokoll-Fenster wird die Funktionsvorschrift dann (mit automatisch vorangestellter Nummer) grafisch aufbereitet dargestellt. Die automatisch vergebenen Nummern können als Abkürzungen verwendet werden: Wurde, wie im Bild, zunächst nur der Funktonsterm eingegeben (und nach Druck auf die Eingabetaste als Ausdruck #1 dargestellt), so kann #2 kurz als „f(x) := #1" definiert werden und wird trotzdem vollständig dargestellt. Die Darstellungsart kann durch im Hintergrund definierte Konstanten dauerhaft beeinflusst werden; per Menü lassen sich Ausmultiplizieren, Faktorisieren und verschiedene andere Arten der Darstellung bzw. Umformung wählen. Die Ausgabe des Funktionsgraphen erfolgt in einem eigenen Fenster, das normalerweise (bei der Vollbildansicht) das Rechenfenster verdeckt. Nach Markieren der zu zeichnenden Funktion bzw. des Funktionsterms im Rechenfenster wechselt man per Button in der Toolbar zunächst ins (2D-)Grafik-Fenster, um dort mit erneutem Knopfdruck den Graphen ins Koordinatensystem zu zeichnen. Eine Möglichkeit, dort ein bestimmtes Flächenstück (wie etwa „die Wiese" aus meiner Aufgabe) schraffiert darzustellen, habe ich nicht gefunden. Auch vordefinierte Funktionen für Ober- und Untersumme scheint es nicht zu geben, aber natürlich lassen sich (wie in #3 gezeigt) Terme für die einzelnen Balken aufstellen und diese dann z.B. zur Untersumme #4 zusammen fassen. Dabei hilft nach dem Markieren von Term #3 und Knopfdruck auf das Summensymbol (aus der Toolbar, die bei aktiviertem linken Fenster auftaucht) ein Assistent: Im Dialogfenster fragt der Assistent den Laufindex sowie dessen untere und obere Grenze ab und erzeugt daraus den Ausdruck #4. Mit dem „ = "-Button („Vereinfachen") findet Derive für die Summe automatisch einen geschlossenen Ausdruck (#5; Umformungen rückt das System automatisch ein). Auch die Aufstellung des Grenzwert-Terms kann leicht per Dialog erfolgen, bei „Vereinfachen" wird der Grenzwert exakt angegeben (und könnte auf Wunsch mit „Approximieren" auch noch in den gerundeten Dezimalwert 13.333333 verwandelt werden). Zum Schluss wurde - wieder mit einem Assistenten, dessen Dialogfenster im Bild zu sehen ist - das Integral berechnet, das natürlich ebenfalls das Ergebnis 40/3 liefert. Ohne Assistent hätte in der Eingabezeile „int(#1,x,0,4)" oder „int(#2,x,0,4)" eingegeben werden müssen, um den Term #1 oder die Funktionsgleichung #2 nach der Laufvariablen x bestimmt von 0 bis 4 zu integrieren.
Das Derive-Protokoll #1 bis #8 im Rechenfenster gibt einen klaren Überblick über die durchgeführten Rechnungen und ihre Ergebnisse; die Ausgabe wird vom Programm automatisch formatiert. Zwar lassen sich über die Eingabezeile auch Bemerkungen, die in Anführungszeichen eingeschlossen sind, als Textzeilen einfügen. Dies eignet sich aber wegen der strengen Form eher für Zwischenüberschriften und kurze Kommentare als für längere Beschreibungen oder verbindenden Text, obwohl (per Toolbar-Button, Menüpunkt Einfügen | Textobjekt oder Hotkey F5) sowohl im Rechenfenster wie im Grafikfenster auch zusätzlich mehrzeiliger Text eingefügt werden kann. Derive ist offenbar eher als Hilfsmittel konzipiert, das neben Papier und Bleistift (oder neben einer Textverarbeitung) als mathematischer Knecht nur für die Mathematik verwendet wird, und dessen Ergebnisse dann von Hand ins Heft oder in das Textdokument übertragen werden. Eine Übertragung einzelner Formeln in die Textverarbeitung mit Kopieren und Einfügen führt im Allgemeinen nicht zu brauchbaren Resultaten: Wie man im Bild sieht, sind die nummerierten Terme wie etwa der markierte Ausdruck #2 im Bild in Wirklichkeit aus mehreren Zeilen mit einfachen Textzeichen zusammengesetzt, die in der Textverarbeitung nach dem Einfügen meist nicht mehr zusammen passen und insbesondere nicht als eine Formel mitten in einer Zeile normalen Textes stehen können. Das gesamte Rechen-Fenster kann aber nicht nur in eigenen Derive-Formaten abgespeichert werden, sondern für die Weitergabe als Textdokument auch in eine reine rtf-Textdatei exportiert werden, die - bei Darstellung in einem mehrzeiligen Textbereich mit fester Zeichenbreite - die Wiedergabe ähnlich der angezeigten Form ermöglicht. Derive installiert eine eigene TrueType-Schrift mit, damit die Ausgabe passt, die in der Art seit Dos-Zeiten praktisch unverändert ist. (Daneben können die Terme noch in die Syntax verschiedener Programmiersprachen exportiert werden). Erzeugte Graphen bzw. Grafikfenster lassen sich hingegen per Zwischenablage bequem als Bilder in andere Dokumente kopieren.
Derive beherrscht die Mathematik (Algebra, Analysis, Stochastik, Vektor- und Matrizenrechnung, Analytische Geometrie sowie komplizierte Funktionen samt 2D- und 3D-Grafik) in einem weit über den Schulstoff hinaus gehenden Umfang und arbeitet schnell und präzise. Die Bedienung ist einfach und kann meist auf verschiedene Arten erfolgen - neben dem Eintippen in die Eingabezeile sind die Dialogfenster der Assistenten nicht nur wie oben beschrieben per Button (Symbol) in der Toolbar (Werkzeugleiste), sondern auch per Hotkey (Tastenkombination) oder per Maus durch Auswahl im Menü erreichbar. Auch lassen sich eigene Funktionen definieren und für die spätere (Wieder-)Verwendung speichern. In der aktuellen Version 6.1 soll es außerdem die Möglichkeit geben, die vom System bei den automatischen Berechnungen ausgeführten Zwischenschritte auf Wunsch abzurufen, um so den Lösungsweg (auch beim Bestimmen von Summe oder Integral?) nachvollziehen zu können. Außerdem kann die neue PC-Version wohl auch Daten mit einigen Derive-bestückten Taschenrechnern (wie TI-89, TI-92+ und Voyager) austauschen.
Insgesamt ist Derive mathematisch ein ausgereiftes Produkt für rasche Rechnungen bzw. Umformungen. Die Software schwächelt allerdings, wenn man nicht nur Graphen und Endergebnisse, sondern auch die Formeln in ein Textdokument übernehmen will - erst Recht, wenn man dabei Wert auf einen vernünftigen Formelsatz legt, bei dem beispielsweise die Schriftgröße von Exponenten kleiner ist als die der Basis.
Zu Derive existiert sehr viel Literatur (u.a. auch wegen des flächendeckenden Einsatzes an Österreichs Gymnasien) und in neueren Schulbüchern und vielen angebotenen Unterrichtsmaterialien findet man zahlreiche Beispiele.
Aus dem Internet konnte eine 6,6 MB große Demo-Version des Programms gratis (und auch ohne Registrierung) zum kostenlosen 30-Tage-Test herunter geladen werden. Inzwischen ist der Vertrieb eingestellt und Ende 2007 sind alle Downloadangebote aus dem Internet verschwunden. Texas Instruments will einen Nachfolger aufbauen, der auf PCs und Taschenrechnern gleichermaßen funktioniert, in Vielem aber offenbar an Derive noch nicht heran reicht. Schade um ein einfach zu bedienendes Programm!
zum Seitenanfang / zum Seitenende
Lösung mit MuPAD Pro 3.1
Erst vor einigen Jahren als Projekt an der Universität Paderborn geboren, wurde MuPAD mit der Version 3.1 inzwischen zu beachtlicher Reife entwickelt. Eine schul- (und vor allem schüler-)gerechte Preispolitik und ein aktives Team, das auf Wünsche der Anwender eingeht und auf dem eigenen Server inzwischen über 400 Arbeitsblätter gesammelt hat, hat zum Erfolg sicher ebenso beigetragen, wie das Konzept der Software: MuPAD ermöglicht das Erstellen eines Arbeitsblatts oder einer Facharbeit in einem Guss, in dem sich Mathematik mit den wesentlichen Funktionen einer Textverarbeitung verbinden lassen. Auch Bilder u.ä. können eingebettet werden, wie z.B. mein Arbeitsblatt „Rotationskoerper_Weinflasche" zeigt. Dabei ist die Bedienung einfach: Geschrieben wird auf der Arbeitsfläche. Wird eine Region als Textbereich deklariert, reagiert das Programm als Textverarbeiter und schreibt den Text wie im gezeigten Beispiel schwarz (oder in der gewählten Farbe) hin. Ist ein Absatz als Eingaberegion gekennzeichnet (erkennbar am roten Punkt am Absatz-Anfang), wird der eingetippte Text rot geschrieben und beim Betätigen der Eingabetaste als Auftrag an das Mathematik-System interpretiert. Das ergänzt dann automatisch die blaue Lösung oder zeichnet die gewünschten Graphen.
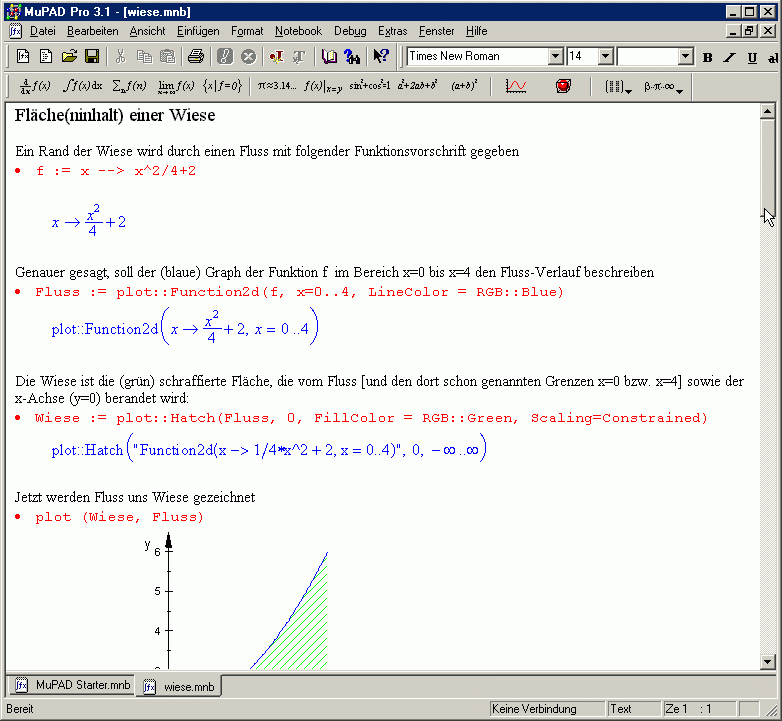
Die roten Mathematik-Eingaben können vollständig zeichenweise eingetippt werden. Tippt man die ersten
Buchstaben eines Befehls, kann man nach Strg+Leertaste aber auch aus einer Liste den passenden Befehl auswählen.
Und häufig verwendete Befehle wie beispielweise für Ableitung, Integral, Summe oder Grenzwert können
bequem durch Betätigen eines Buttons in der Toolbar abgerufen werden (und müssen dann nur noch an ein paar
Platzhaltern ergänzt werden). Ein umfangreiches Hilfesystem mit ausführlichen Erläuterungen zu jedem
Befehl jeweils einschließlich (kopierbarer) Beispiele hilft bei der richtigen Syntax. Schade allerdings:
Weiß man nicht ungefähr, wie der Befehlsname anfängt, wird's gelegentlich schwierig -- bei der Suche
nach den Stichwörtern „schraffiert", „Schraffur" oder „Flächenstück" lieferte die
Hilfe keinen Treffer. Wer hätte schon nach 'Hatch' gesucht?! Diese Möglichkeit hatte ich
zufällig in einem fremden Arbeitsblatt entdeckt und übernommen, um die Wiese grün zu schraffieren.
Außerdem ist interessant, dass die Graphen wie oben etwa Fluss und Wiese eigenständige Objekte bilden und
„vorab" definiert werden können, aber erst nach dem Aufruf z.B. von plot (Wiese, Fluss) wirklich
gezeichnet werden (Scaling=Constrained bedeutet dabei, dass x- und y-Achse in gleichem Maßstab geteilt
werden).
Schön: mit der mitgelieferten student-Bibliotheksfunktion plotRiemann können Unter- und Obersummen gezeichnet und berechnet werden.
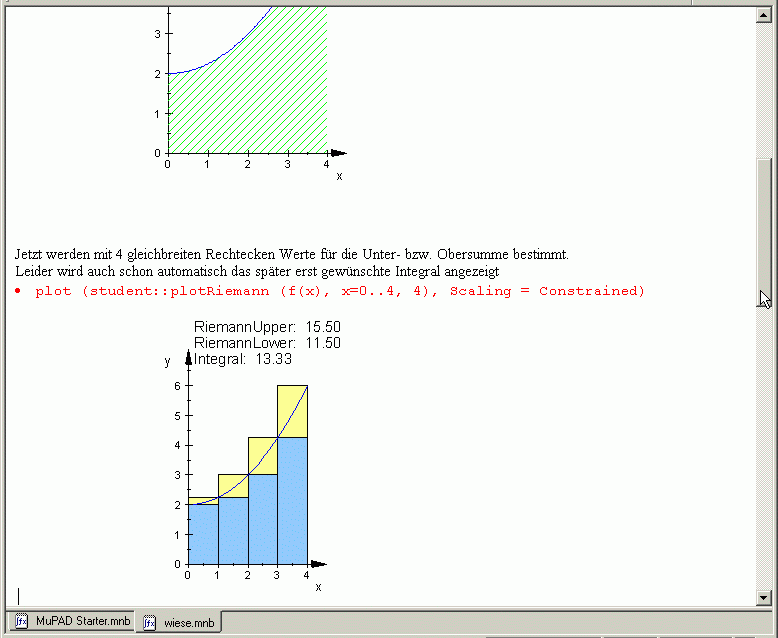
(Da das ganze MuPAD-Dokument mit der Ausgabe mehrere Bildschirme umfasst, obwohl vom Anwender nur wenige Zeilen eingegeben werden mussten, kann der vollständige Abdruck als pdf-Dokument (85 kB) hier in einem eigenen Fenster geöffnet werden. Darin sieht man auch automatisch erzeugte, typografisch ansprechende Summenformeln, die sich auch einzeln [als Bilder] in Textdokumente übernehmen lassen. Außerdem findet sich dort die symbolische Grenzwert- und Integralberechnung sowie das Beispielfoto einer Hilfeseite!) .
MuPAD beherrscht die Mathematik wohl in ähnlichem Umfang wie Derive (Algebra, Analysis, Lineare Algebra, Stochastik und analytische Geometrie) - in der MuPAD-Schriftenreihe „Mathematik 1x anders" [kostenlose pdf-Fassungen auf dem MuPAD-Internet-Server] werden hierzu und zu weiteren Gebieten Beispiele und Anwendungsmöglichkeiten vorgestellt.
Die Software erfordert zwar eine gewisse Einarbeitung bzw. Gewöhnung an das Konzept; die vielen auf http://www.sciface.com/education/material.php erhältlichen Beispiele, Broschüren und Materialien helfen allerdings sehr. Gelegentliche e-Mail-Rückfragen an das MuPAD+Schule-Team wurden zudem schnell und gut beantwortet. Außerdem nimmt die Verbreitung offenbar rasch zu, so dass auch von dritter Seite bald noch mehr Unterstützung zu erwarten ist. Insbesondere werden Schülerinnen und Schüler ermutigt, ihre Facharbeiten mit MuPAD zu schreiben, wofür es kostenlos eine zeitlich befristete Lizenz gibt. Wird die Arbeit gut oder sehr gut, wird dem Schüler bzw. der Schülerin eine Lizenz geschenkt. Und verfügt eine Schule bereits über eine Campus-Lizenz, können Schülerinnen und Schüler eine eigene Lizenz für zu Hause für nur 15 € erwerben.
Aus dem Internet kann jede(r) eine 30-Tage-Demoversion (44 bzw. 60 MB) zum kostenlosen Ausprobieren herunter laden (s.u.; Tabelle). Außer für Windows ist MuPAD auch für Mac und Linux verfügbar. Hervorzuheben ist noch, dass erstellte Arbeitsblätter (die als Notebooks bezeichnet werden) auch als html-Webseiten oder als rtf- und doc-(= MS Word-)Dokumente exportiert werden können. Animationen können als animierte Gif-Bilder oder AVI-Video-Sequenzen mit exportiert werden. Zur Zeit sind offenbar Ergänzungen in Arbeit, die auch in Word bzw. in veröffentlichten Webseiten einen Teil der mathematischen Funktionalität ermöglichen und noch mehr Layout-Möglichkeiten bieten, aber auch Berechnungen bzw. Umformungen durch die Besucher einer Webseite.
Ein kostenlos herunter ladbares zusätzliches 'Schrittrechner'-Package ermöglicht angeblich jetzt schon MuPAD-Besitzern bei einigen Rechnungen, insbesondere beim Lösen von Gleichungen, die Ausgabe von Zwischenschritten, um so den vom Programm gewählten Lösungsweg zu verdeutlichen.
zum Seitenanfang / zum Seitenende
Lösung mit GeoGebra 2.5.1
Das wohl neueste hier besprochene Produkt ist die in letzter Zeit mehrfach ausgezeichnete, offenbar an der Uni Salzburg entwickelte Software GeoGebra, die völlig kostenlos erhältlich ist und gratis verwendet werden darf (GNU General Public License). Das Programm verbindet Algebra und elementare Geometrie, kann also vor allem viel, was man sonst in Programmen wie Euklid-DynaGeo oder dem kostenlosen Zirkel und Lineal (Z.u.L) findet (s.u., „Weitere Software und Hinweise"). Es ist kein CAS-Programm im strengen Sinne, hat aber - obwohl das nicht der Schwerpunkt von GeoGebra ist - einige Fähigkeiten, mit denen sich die oben gestellte Aufgabe lösen lässt. Im getesteten Analysis-Bereich gehen die Fähigkeiten nicht über den Schulstoff hinaus; sichere symbolische Umformungen werden nur für Polynome versprochen, klappen aber zum Teil auch bei Exponential- oder gebrochen-rationalen Funktionen. Das objektorientierte Konzept unterscheidet sich von den beiden vorgenannten Programmen: Wird z.B. eine Funktionsgleichung eingegeben, so nimmt GeoGebra die Funktion nicht nur in den Objektbestand auf, sondern zeichnet sofort und automatisch den Graphen (es sei denn, man entfernt extra das Häkchen vor „Objekt anzeigen" in den Objekteigenschaften). Lässt man ein Integral berechnen, werden bei der Standardeinstellung die zugehörigen Flächenstücke im Graphen automatisch eingefärbt.
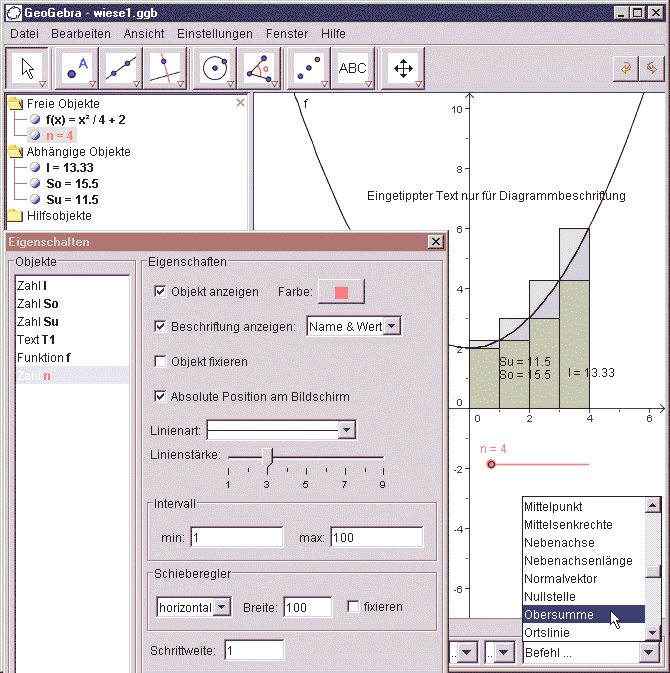
Für die Lösung der oben genannten Aufgabe mit einer Wiese muss (in eine spezielle, am unteren Fensterrand befindlichen Eingabezeile, die im Bild leider gerade vom Dialog-Fenster 'Eigenschaften' verdeckt ist) zunächst die Funktionsvorschrift eingetippt werden: „f(x) = x^2/4+2". Beim Betätigen der Eingabetaste wird die Funktion dann im linken (Objekt-)Fenster als 'Freies Objekt' aufgenommen und gleichzeitig sofort im rechten (Grafik-)Fenster gezeichnet. Um später 4 (oder auch eine andere Anzahl n von) Streifen für die Unter- bzw. Obersumme zu zeichnen, erfolgt als Zweites die Eingabe „n=4". Danach wird „So = Obersumme[f,0,4,n]" eingegeben, um automatisch die Obersumme für die Funktion f im Bereich 0..4 mit n Streifen zu berechnen (das Ergebnis So = 15.5 erscheint links) und zu zeichnen (rechts erscheinen vier Streifen, die transparent eingefärbt sind, sodass später auch die Markierungen für die Untersumme und das Integral trotz Überdeckung ebenfalls sichtbar sind. Der ebenfalls rechts angezeigte Zahlenwert kann mit der Maus verschoben werden, um gut erkennbar zu sein). Statt die Eingabe vollständig zeichenweise einzutippen, hätte das Wort Obersumme auch aus einer Befehlsliste rechts neben der Eingabezeile gewählt werden können (s. Bild); außerdem versucht das System nach erkannten ersten Zeichen Befehle auch automatisch zu vervollständigen. In gleicher Weise kann die vierte Eingabe „Su = Untersumme[f,0,4,n]" mit dem selbstgewählten, beliebigen Namen Su erfolgen (ohne Zuweisung an eine Variable hätte GeoGebra die Ergebnisse a=15,5 und b=11,5 genannt). Und die fünfte Eingabe „I = Integral[f,0,4]" führt zur Berechnung des Integrals und dem Tönen der entsprechenden Fläche unterm Graphen. Dass das Ergebnis I=13.33 im linken Fenster vor der Unter- und Obersumme steht, liegt daran, dass im Objektbaum die Objekte offensichtlich alphabetisch und nicht chronologisch angeordnet werden.
Mit wenigen, einfachen Befehlen konnte hier die Aufgabe weitgehend gelöst werden. Allerdings sucht man in GeoGebra vergeblich einen Befehl, um einen allgemeinen Term für die Unter- bzw. Obersumme aufzustellen bzw. anzuzeigen und/oder eine algebraische Grenzwertbetrachtung durchzuführen. Dafür kann im Objektbaum die Zeile n=4 mit der rechten Maustaste angeklickt werden, woraufhin sich der abgebildete Eigenschafts-Dialog öffnet. Dort kann gewählt werden, dass das Objekt n als Schieberegler angezeigt wird (rot im Grafikfenster) und mit der Schrittweite 1 beispielsweise zwischen 1 und 100 variiert werden darf. Betätigt man dann später mit der Maus diesen Schieberegler, so wird automatisch grafisch die Zerlegung mit der neu eingestellten Streifenzahl und links die aktuellen Ergebnisse von Unter- und Obersumme angezeigt, sodass man auch hier die Konvergenz der Werte veranschaulichen bzw. erfahren kann!
Auch wenn sie beim Lösen der Test-Aufgabe nicht unbedingt benötigt wird, soll unbedingt auf eine sensationelle Eigenschaft von GeoGebra hingewiesen werden: Als Kombination aus dynamischer Geometrie-Software und CAS-System konzipiert, hängen Funktionsvorschrift und Graph in beiden Richtungen zusammen: Es wird nicht nur, wie oben erwähnt, zu einem eingegeben Term automatisch der Graph erzeugt. Umgekehrt kann man auch mit der Maus die Parabel verschieben - und automatisch wird der Funktionsterm verändert(!), werden Unter-, Obersumme und Integral zahlenmäßig aktualisiert. GeoGebra gelingt es so, die Äquivalenz verschiedener Repräsentationen eines mathematischen Objekts automatisch zu veranschaulichen.
Dem Programm ist eine gut verständliche Dokumentation mit Beispielen (als pdf-Datei) beigegeben. Der Autor hat auf http://www.geogebra.org/cms/ unter Hilfe u.a. ein Benutzerforum eingerichtet; außerdem gibt es viele Hundert fertige Beispiele und Materialien und auf GeoGebraWiki kann man auch eigene GeoGebra-Unterrichtsreihen und -beispiele hoch laden kann, um sie der Öffentlichkeit zur Verfügung zu stellen. Insofern kann auch hier auf viele Beispiele und Erfahrungen anderer zurück gegriffen werden.
GeoGebra eignet sich - anders als MuPAD - zwar nicht, um damit ganze Arbeitsblätter zu erstellen. Andererseits ist die Bedienung sehr einfach und neben den besonderen Möglichkeiten des Programms (Verwandlung von Gleichungen in Graphen und umgekehrt; Interaktion per Schieberegler,...) sind auch die Exportmöglichkeiten beachtlich: Die Ergebnisse können als Bilder, bei geometrischen Konstruktionen auch als Konstruktionsprotokoll sowie als dynamische Webseiten (wo etwa der Besucher der Webseite den Schieberegler betätigen kann und so die Streifenzahl und die Ergebnisse verändert) exportiert werden!
GeoGebra ist in Java geschrieben und läuft auf allen Plattformen, auf denen Java 1.4.2 verfügbar ist. Der Download der GeoGebra-Software umfasst nur 2,5 MB.
zum Seitenanfang / zum Seitenende
Tabelle mit wichtigen Daten der 3 Programme
| Derive | MuPAD Pro | GeoGebra | |
| im April/Mai 2005 getestet | 5.06 | 3.1.0 | 2.51 |
| aktuelle Version Mai 2005 | 6.1 | 3.1.1 | 2.51 |
| Nachtrag: letzte Version im Juni 2009 |
Der Vertrieb von Derive wurde Ende 2007 ohne vergleichbaren Nachfolger eingestellt! | 4.0.6 - Der Vertrieb von MuPAD wurde im Sept. 2008 eingestellt. Es wird künftig in 'MATLAB and Symbolic Math Toolbox' integriert. | 3.2 |
| Hersteller/Vertrieb Webadresse |
Texas Instruments www.derive-europe.com |
SciFace www.mupad.de |
Markus Hohenwarter www.geogebra.org |
| 30-Tage-Demo gratis erhältlich | ja | ja | ja (Vollversion) |
| Downloadgröße (Mai 2005) | 6,6 MB | 44...60 MB | 2,5 MB |
| Preise (Ende Mai 2005) für - Einzellizenz - Schullizenz - Schülerzusatzlizenz |
199 € (bzw. 84 € für Stud./Lehrer) 399 € (1198 € inkl. Schüler) 19 € |
120 € (Lehrer) / 80 € (Stud.) 408 € (986 € inkl. Schüler) 15 € |
kostenlos (0 €) kostenlos (0 €) kostenlos (0 €) |
| eigener Server für Unterrichtsmaterialien | -- | Seit Oktober 2008 nur noch mupad.zum.de. Achtung: Service endet am 1.8.2009! | http://www.geogebra.org/de/wiki |
| Eingabe | Eingabezeile | Seite (Text- oder Eingaberegion) | Eingabezeile |
| Eingabehilfe / Assistenten | vorhanden | vorhanden | vorhanden |
| Einfügen von Bildern und OLE-Objekten*) | möglich (ins Rechenfenster) | möglich (an beliebiger Stelle auf der Seite innerhalb einer Textregion) | nur Bilder (auch als Hintergrund) ins Graphikfenster („Zeichenblatt") |
| Import (außer eig. Dateiformat) | -- | rtf- oder doc-Dokument(e) | -- |
| Export (außer eig. Dateiformat) | einfacher rtf-Text, Programmiersprachensyntax | rtf- oder doc-Dokument oder html-Webseite mit Bildern; Programmtext | dynamische html-Webseite (mit Applet), Konstruktionsprotokoll |
| Besonderheiten | altbewährte und bekannte Software, leider seit 2007 nicht mehr erhältlich | vielfältige Möglichkeiten; Erstellen von Übungsblättern, Artikeln u.ä. „in einem Guss" | algebraische Darstellung bidirektional verknüpft mit dynam. Geometrie; Java erforderlich |
| Besprechung (Aufgabenstellung) | Lösung mit Derive | Lösung mit MuPAD | Lösung mit GeoGebra |
*) OLE-Objekte sind Dokumente anderer auf dem eigenen Computer registrierter Programme, z.B. Excel-Tabellen, Powerpoint-Präsentationen, Videos, Bilder des Bildbearbeitungsprogramms, u.ä. In das Mathe-Programm (Derive oder MuPAD) wird ein kleines Bild z.B. einer Excel-Tabelle eingebettet; mit Doppelklick darauf kann man dann Excel öffnen und die Tabelle ansehen/nutzen oder bearbeiten. Analoges gilt für die Dateien anderer Programme.
zum Seitenanfang / zum Seitenende
Weitere Software und Hinweise
Die von MuPAD aufgegriffene Idee, Text und Mathematik zu verbinden, ist nicht neu. So wird dieses Konzept schon
lange von MathCAD (www.mathcad.com) verwirklicht (bei MathCad
lassen sich normaler Text und Formeln bzw. Berechnungen sogar innerhalb einer Zeile mischen - bei MuPAD braucht man
dazu Word und das zusätzlich vom MuPAD-Hersteller käuflich erhältliche Word-AddIn MuPAD für Word)). Der Vertrieb hat aber (z.B. mit ingenieurwissenschaftlichen
Zusatzpaketen) bisher eher industrielle Anwender angesprochen und sich kaum um Schulen bemüht. Der Preis von 869
€ (z.B. bei www.softline.de im Mai 2005) allein für
eine Einzellizenz vom MathCAD 12 überfordert Schulen wohl auch im
Allgemeinen, wenngleich gelegentlich ältere Versionen als preisgünstige Student's Editions erscheinen und
eine abgespeckte Version 8 im Dezember 2003 mal kostenlos auf der Heft-CD der Zeitschrift „PC Professionell" zu
finden war. Auf http://www.schulphysik.de/mathcad.html nennt Herr Krahmer allerdings günstigere Preise und zeigt
und verweist auch auf MathCad-Beispiele.
Eher im Universitätsbereich anzutreffen und ebenfalls mit abschreckender Preispolitik (die Einzelversion von
Maple 10 Professional kostet 1245 US-$, obwohl im Rahmen eines
High-School-Programms jetzt Studenten-/Schüler-Versionen ab 125 $ verkauft werden - Materialien und
Kursunterlagen kosten jeweils extra) ist das ebenfalls schon lange am Markt befindliche und offenbar recht
leistungsfähige Maple (www.maplesoft.com), das hier nur der Vollständigkeit halber
erwähnt wird.
Hingewiesen sei auf die Webseiten des österreichischen Zentrums für die Didaktik von Computeralgebra unter http://www.acdca.ac.at/. Literatur zu CAS-Programmen für die Schule, insbesondere zu Derive, gibt es u.a. bei bk-teachware.com.
In Deutschland finden sich Besprechungen, Beispiele und lohnenswerte Hinweise u.a. auf den Mathe-Seiten von lehrer-online sowie an vielen Stellen im sehr umfangreichen, manchmal etwas verwirrenden Webangebot von Dörte Haftendorn (die u.a. mit MuPAD, GeoGebra und Euklid-DynaGeo arbeitet), sowie - übersichtlich, aber nicht ganz aktuell - bei learn-line (siehe dort Auswahlmenü am rechten Rand). Die konkrete Suche im Internet fördert jede Menge weiterer Seiten und Angebote zu Tage.
Trotz Suche konnte ich allerdings die früher einmal hier erwähnte Java-Bibliothek HartMath für symbolisches Rechnen von Klaus Hartlage nicht mehr im Web finden - vermutlich ist sie nicht mehr public domain. Eine Vielzahl fertiger interaktiver mathematischer Java-Applets ist aber auf der japanischen, zum Glück englischsprachigen Seite JAVA - Manipula for Math verfügbar.
Die bei der Besprechung von GeoGebra erwähnten dynamischen Geometrie-Programme gibt es bei http://www.dynageo.de (Euklid-DynaGeo; im Mai 2005 gabs die Version 2.6e mit ca. 2,1 MB Downloadumfang als Shareware; Einzellizenz 29 €, Schullizenz 87..145 €) bzw. http://www.ku-eichstaett.de/Fakultaeten/MGF/Mathematik/Grothmann/Software.de oder www.z-u-l.de (Zirkel und Lineal Z.u.L., im Mai 2005 Version 3.71 mit ca. 3,8 MB Downloadgröße, kostenlos, Java erforderlich). Sie werden auf Seite d) meiner Besprechungen miteinander verglichen (dort auch Hinweise auf aktuelle Versionen)!
Und Literatur zum Einsatz von Derive und MuPad in der Linearen Algebra und Vektorgeometrie wird auf der Seite e) meiner Mathe-Software-Besprechungen angegeben.
zurück zur „Mathematik"-Hauptseite