| www.r-krell.de |
| Webangebot für Schule und Unterricht, Software, Fotovoltaik und mehr |
Willkommen/Übersicht > Mathematik >
Rezension von Mathematik-Software, Teil b2) :
Interaktive Lern- und Nachhilfeprogramme
S II
Auf diesen Seiten berichte ich über meine Erfahrungen mit bzw. meine Eindrücke von verschiedenen Mathematik-Programmen, nämlich:
a) numerische Programme: Rechen- und Zeichenhilfen
b) interaktive Programme: Lern- und Nachhilfe-Programme
c) Computer-Algebra-Systeme (CAS): genaues und symbolisches Rechnen, Termumformungen und Zeichnen
d) Dynamische Geometrie-Software (DGS): geometrisches Konstruieren, Abbilden, Bewegen und Messen
e) Software zur Linearen Algebra und zur Vektorgeometrie
zum Seitenanfang / zum Seitenende
Rezension von Mathematik-Software
b2) interaktive Programme:
Lern- und Nachhilfe-Programme für die S II
Diese Gruppe von Programmen ist vor allem für Schülerinnen und Schüler etwa der Klassen 10 bis 13 gedacht, die zu Hause mathematische Teilgebiete wiederholen, üben, nachholen oder vertiefen wollen. Die Software kann aber oft auch begleitend (z.B. in Übungsphasen) im Unterricht eingesetzt werden oder vom Lehrer oder der Lehrerin bei der Unterrichtsvorbereitung als Quelle für Aufgabenmaterial herangezogen werden.
Die Programme wurden in den Jahren 1999 bis 2001 z.T. preisgünstig (reduzierte Restauflagen) gekauft und daher noch in DM bezahlt: 1 DM sind umgerechnet rund 0,5 €uro bzw 1 € = 2 DM. Es folgen die Besprechungen im Einzelnen:
zum Seitenanfang / zum Seitenende
Klar abraten muss ich vom Mathematik-Baukasten, den es im Jahr 2000 für 39,95 DM beim Weltbild-Verlag gab (Tel. 0180-5354321, Bestell-Nr. 601815) und der später im Buchhandel im Franzis-Karton zu kaufen war. Das Windows-Programm wird als interaktives Programm zum kreativen Experimentieren mit Mathematik angeboten. Die offenbar im/vom Franzis-Verlag entwickelte Software erwies sich als eine dürftige Sammlung verschiedener kleinerer Programme, u.a. einem Zeichen- bzw. Malprogramm, das weniger konnte, als das in Windows enthaltene Paint (oder Paintbrush). Dafür wurde auf kariertem Papier statt auf einer einfachen weißen Zeichenfläche gezeichnet. Konstruktions-Befehle, wie sie in CAD- oder Geometrie-Programmen üblich sind, fehlten. Andere Teil-Programme konnten einfache Rechnungen durchführen oder Graphen zeichnen, blieben aber weit hinter dem Funktionsumfang der im Teil a) besprochenen Programme zurück. Die Interaktivität beschränkte sich auf das Eingeben von Zahlen bzw. der Funktionsterme und war nirgends besser als in den oben vorgestellten Programmen. „Jetzt können Sie in photorealistischen 3-D-Laboratorien fröhlich experimentieren!" heißt es irreführend in der Werbung. Wenn die Software nicht entscheidend verändert wurde, bezieht sich diese Aussage nur auf das Titelbild: In der perspektivischen Ansicht eines Zimmers mit Schreibtisch kann man entweder auf einen dort liegenden Taschenrechner oder ein Zeichenbrett klicken, um die entsprechenden Programmteile zu starten. Beim Taschenrechner wird der aus Windows gestartet! Erst nach Abschluss jedes Teilprogramms (das jeweils ohne Laboratmosphäre auskommt) findet man sich wieder im 'fotorealistischen' Zimmer, das man mit einem Klick auf die Tür auch ganz verlassen kann, um so den Mathematik-Baukasten zu beenden. Möglicherweise ist das die gelungenste Funktion dieser enttäuschenden Software. In der gleichen Reihe gibt's noch mehr Baukästen.
zum Seitenanfang / zum Seitenende
Mathematik interaktiv / Telekolleg II: Analysis - Differentialrechnung von der TR Verlagsunion/Rossipaul (in Zusammenarbeit mit der ARD-Sendereihe Telekolleg) bietet hingegen die versprochene Interaktivität: Es möchte Wissen über die Analysis vermitteln oder zumindest vertiefen und konkurriert so mit den von vielen Verlagen herausgegebenen Schülerhilfen oder Trainingsbüchern zur Analysis. Funktionsgrenzwerte, das Tangentenproblem (von der Sekanten- zur Tangenten- bzw. Graphen-Steigung), Ableitungen und Ableitungsregeln (auch Produkt-, Quotienten- und Kettenregel) sowie Extremwertaufgaben werden behandelt. Neben einem einführenden, z.T. animierten Lehrtext („Darstellung") können und müssen Beispiele am Bildschirm gelöst werden („Übungen"). Zum Teil muss die richtige Reihenfolge der Schritte angegeben werden oder es müssen -- bei den meisten Aufgaben -- innerhalb einer vorgegeben Schrittfolge Terme aufgestellt, umgeformt, berechnet und eingegeben werden. Bei Problemen können Tipps (meist die entsprechende Regel mit zusätzlichem, ähnlichen Beispiel) oder auch die richtige Lösung abgerufen werden.
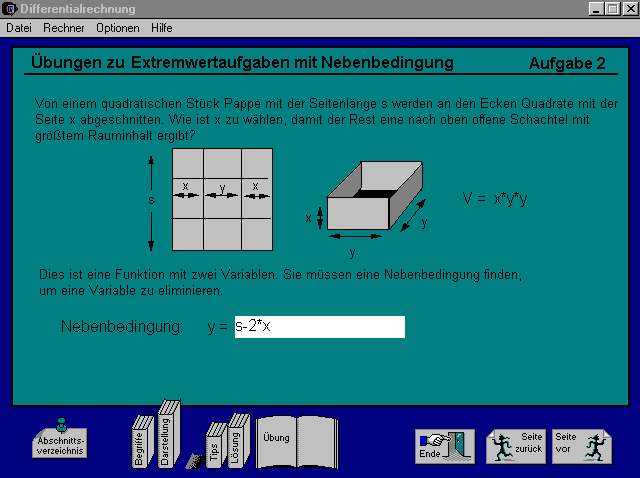Während die Schrittfolge und damit der Lösungsweg leider starr fest liegen, ist das Programm bei den Eingaben erstaunlich flexibel: Wird
z.B. wie bei der dargestellten Extremwertaufgabe nach dem Volumen V = x2*y einer Kiste gefragt, so erkennt das Programm Eingaben
wie x*y*x oder yx^2, aber auch 0,5*y*2x^2 als richtig an.
Zu den meisten Bereichen können beliebig viele, zufällig erzeugte Übungsbeispiele (im üblichen Lehrbuchstil) abgerufen werden; lediglich bei den Extremwertaufgaben gibt's nur 4 feste Aufgaben, die allerdings recht unterschiedlich und ansprechend sind. Der Dialog mit dem Programm zwingt vermutlich eher zum Lernen als ein Buch -- zumindest bei computerbegeisterten Jugendlichen.
Wegen der Möglichkeit der Formeleingabe (alle anderen hier besprochenen Programme bieten nur die Mehrfachauswahl oder gelegentlich Zahleneingaben) und des klaren Aufbaus hat mir dieses Programm am besten von allen hier vorgestellten Programmen gefallen!
Insgesamt halte ich das Programm auch für Schülerinnen und Schüler für eine gelungene Alternative zu einem gedruckten Trainingswerk. Es kommt auf zwei 3,5"-Disketten für Windows 3.1 (läuft auch unter Win 95/98) und gab's im Sommer '99 für knapp 20,- DM (Best.-Nr. SA-748-01 bei Pearl, Tel. 0180-55582). Auch zu anderen Themenbereichen der Mathematik werden in der gleichen Reihe Programme angeboten (z.B. „Telekolleg Rechentechniken" im Oktober '99 bei Pearl für nur 8,80 DM, Best.-Nr. SA-719-04).
zum Seitenanfang / zum Seitenende
Differential- & Integralrechnung (V 1.1, Bd. 2 aus der Reihe 'Multimedia Mathematik' im Franzis-Verlag, (C) Tedata 1996): Das Programm wendet sich -- obwohl unter der Überschrift „Lernen kann auch Spaß machen!" angeboten -- eher an Mathematik-Studentinnen und -Studenten der ersten Semester, weniger an Schüler. Wegen der Inhalte, der oft anspruchsvollen Beispiele und des doch recht hohen Formalisierungsgrades in der Darstellung/Sprechweise könnte es höchstens begleitend im (Leistungskurs-)Unterricht eingesetzt werden. Da sind auch die kleinen Trickfilme, z.B. über nicht-differenzierbare Funktionen (wie f(x) = |x| oder g(x) = x sin(1/x) jeweils bei xo = 0) hilfreich.
Dabei ist die Fülle des behandelten Stoffes beeindruckend. Neben üblichem Schulstoff einschl. Integration durch Substitution und partielle Integration findet man auch Differential, implizite Funktionen, Funktionen in 2 Variablen; bei der Integration auch Doppelintegrale, Kurvenlänge, Volumen und Mantelflächen von Rotationskörpern, sowie einige physikalische Beispiele (Dichte und Schwerpunkt eines inhomogenen Stabes, Stromfluss [leider fließen die Elektronen im Film in Stromrichtung], Arbeit im Radialfeld, Spannarbeit, Radioaktiver Zerfall, u.a.).
Bei den Aufgaben kann zur Hilfe neben der vorgerechneten Lösung oft noch die allgemeine Vorgehensweise per gesprochenem oder geschriebenem Text abgerufen werden; zu den Übungen gibt es wahlweise Theorieverweise (auf Kapitel im Lehrtext), Grafikhilfe (z.B. Graph von Funktion und Ableitung), Analysishilfe (einige wichtige Rechenschritte oder Umformungen, die benutzt werden müssen) oder Tutorverweise (ähnliche Aufgaben mit kommentierter Lösung). Die Ergebnisse der vielen Übungen, die offenbar auf einem Blatt gemacht werden sollen und z.T. längere Rechnung erfordern, werden aber nicht ins Programm eingegeben, sondern müssen vom Benutzer mit der richtigen Lösung verglichen werden. Für die Statistik kann man nur richtig oder falsch markieren. Die Software ist gut programmiert, flüssig im Ablauf und die Navigationsmöglichkeiten sind sehr gut und übersichtlich gelöst. Im Oktober 1999 noch für 29,95 DM, jetzt im Februar 2000 für nur noch 14,95 DM (Best.-Nr. 8019-185 bei SMM.) gut als Nachschlagewerk bzw. zur Unterrichtsergänzung für Lehrerinnen und Lehrer oder zur Abiturvorbereitung von Leistungskursschülerinnen und -schülern geeignet, aber meiner Meinung nach eben kaum als Training für Schüler der 11. Klasse.
zum Seitenanfang / zum Seitenende
Extremwerte (1997, aus der Reihe 'Leicht gelernt' des Hemming-Verlags): Zwar bietet dieses Programm („ab 14 Jahren") nach langem, bunten Vorspann auch einige Seiten Geschichte, Anwendungsbereiche (nur kurze Texthinweise), Theorie, Grundlagen und Formelsammlung. Aber diese Themen wurden nur pflichtmäßig mehr schlecht als recht, trocken und viel zu knapp abgehandelt, lediglich eine (nicht animierte) Graphenserie jeweils von f, f' unf f" zur Verdeutlichung der Kriterien bei der Kurvendiskussion ist ganz nett. Kernpunkt der Software sind eindeutig die 50 Extremwertaufgaben, nach unerfindlichen Kriterien in 10 Gruppen à 5 Aufgaben geordnet, und als „Praktische Anwendungen" betitelt. Als Vorbereitung gibt's zuvor in den „Grundlagen" eine Musteraufgabe mit kompletter Lösung und vier Übungen nur für Nebenbedingungen.
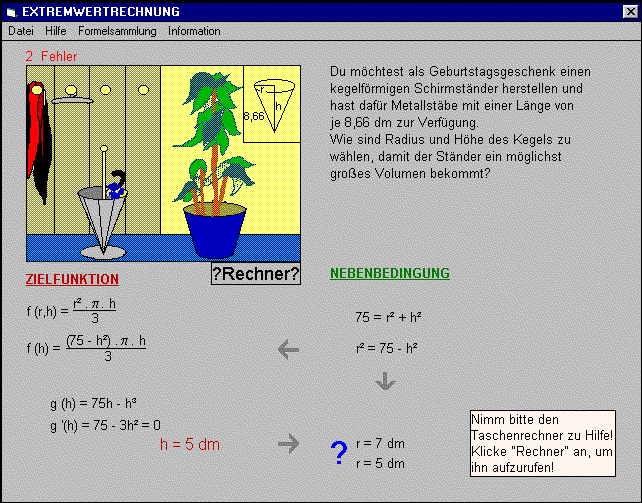Die überwiegend interessanten Aufgaben entstammen vielen Bereichen und sind ansprechend verpackt. Die
Lösung geschieht am Bildschirm, wobei der Lösungsweg strikt geführt ist: nach der Reihe werden
Nebenbedingungen, Zielfunktion, Umformungsschritte und Ableitung abgefragt, wobei jeweils eine von
zwei vorgegebenen Alternativen anzuklicken ist. Die erreichbare Hilfe ist eher spärlich (kontextabhängig
u.a. Übersicht über die Ableitungsregeln oder sehr allgemeine Grundsätze zum Finden einer Zielfunktion
oder Aufstellen einer Nebenbedingung). Wird die falsche Alternative gewählt, weist oft ein kurzer Text auf
die mögliche Fehlerursache hin, allerdings fehlen Erklärungen z.B. der gewählten Bedingungen oder Ansätze. Dafür gibt's gelegentlich sogar Modellkritik: nach dem ein volumenmaximierter Schirmständer plötzlich
1,4 Meter breit wird, erscheint die Frage, ob wohl nach diesem Kriterium Ständer hergestellt werden sollten (ohne Antwort[-möglichkeit]).
Leider verleitet das Programm dazu, sich ohne viel Nachdenken durch die Alternativen zu klicken, zumal keine weitere Interaktion möglich ist. Bei den schönen Aufgaben eigentlich schade.
Die Software läuft problemlos von CD (Vorsicht: das automatische Setup kopiert nicht das Programm auf die Festplatte, sondern überschreibt gnadenlos einige auf fast allen Rechnern längst vorhandene DLLs mit alten Versionen von der CD). Bei höheren Bildschirmauflösungen wird trotzdem nur ein 640x480-Pixel-Bereich in der Mitte genutzt. Die Navigationsmöglichkeiten sind unzureichend: man kann nicht einfach eine Seite zurückblättern, sondern muss vom Kapitelanfang wieder vor. Andererseits sind die technischen Unzulänglichkeiten bei einem Preis von nur noch 5,95 DM sicher zu verschmerzen. Wer (auch als Unterichtende[r]) viele Extremwertbeispiele sucht oder als Lernende[r] massenweise Aufgaben üben will und genug Disziplin mitbringt, nicht einfach nur zu klicken, sollte diesen Betrag ruhig riskieren (Ende 1999 für 5,95 DM als Best.-Nr. 5050-176 bei SMM).
zum Seitenanfang / zum Seitenende
Mathe Tutor Oberstufe (Version 1, (C) Maaß/Stöckel, 1997, im Vertrieb von Koch Media): Dieses Programm unterscheidet sich von den drei anderen
vor allem in der Art des Zugangs: MUED-gemäß (vgl. meine Mathematik-Seite) werden Anwendungen nicht nur als kleinere Verbrämungen der Fachsystematik verstanden, sondern das Mathematisieren selbst, also der ganze Weg von einem Alltagsproblem hin zu einer mathematischen Fragestellung sowie --
nach erfolgter mathematischer Lösung, die natürlich auch dazu gehört -- die anschließende Rückführung des Rechenergebnisses in eine Alltagslösung
einschließlich kritischer Reflexion des Modells, soll mit dieser CD erlernt oder zumindest geübt werden.
Die Hauptauswahl enthält 4 Alternativen: Lernmodule, Übungsbeispiele, Wissensstand und Projekte.
Die Lernmodule sollen offenbar zunächst die benötigten Fähigkeiten trainieren: Themen wie die Einführung des Differenzierens (z.T. schön animiert mit beweglicher Tangente an einem Graphen) und einer -- leider sehr textbasierten -- Erklärung der Intervallschachtelung finden sich hier ebenso wie jeweils ein ausführlich erläutertes Beispiel zur Kurvendiskussion und zu Extremwertaufgaben. Bei der Extremwertaufgabe werden die einzelnen Lösungsschritte fragend-entwickelnd geführt und gut erklärt -- insofern mag sich das Programm wirklich als Nachhilfe-Lehrer eignen, wie Verlag und Titel behaupten. Leider lassen sich bei vielen gestellten Fragen aber keine eigenen Antworten eingeben, das Programm spricht und nennt auf Mausklick ein paar Möglichkeiten. Offenbar wird erwartet, dass der Benutzer sich zuvor auf Papier um eine eigene Lösung bemüht hat und diese nur noch vergleicht. Auch bei der Aufforderung „Zeichnen Sie.." liefert ein Klick schon den fertigen Graph als (Kontroll-)Lösung. Über den mathematischen Teil hinaus gibt's aber auch Hinweise zur Modellbildung (z.T. gesprochen) und zum Textverständnis, wobei in den Lernmodulen allerdings im Wesentlichen Übersetzungen von Text in Formeln vorgeführt werden.
Mehr Benutzer-Aktivität ist dann bei den Übungsbeispielen gefragt: Hier können offenbar beliebig viele Ableitungen
gefragt werden, wobei die richtige Antwort jeweils aus mehreren Alternativen ausgewählt werden muss. Die Auswahl
wird mit Geräuschen kommentiert, bei falscher Auswahl werden meist mögliche Ursachen (z.B. „Sie haben die Exponenten falsch berechnet") genannt. Leider wird dann sofort die richtige Antwort gezeigt, so dass andere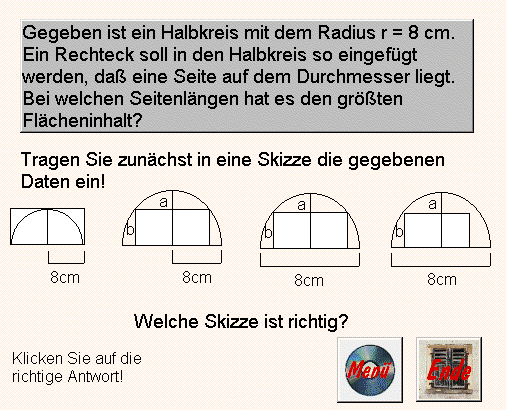 
Alternativen wohl
nicht mehr probiert werden -- schade, wenn der Schülerin oder dem Schüler eine Antwort schon als so wahrscheinlich
erschien, dass genauere Überlegungen nicht mehr angestellt und die restlichen Alternativen noch nicht geprüft wurden.
Weiterhin gibt es bei den Übungen drei Aufgaben, in denen eine vollständige Kurvendiskussion verlangt wird. Hier
sollen auf einem Blatt notierte Ergebnisse zur Kontrolle in das Programm eingegeben werden, d.h. berechnete Null-, Pol-,
Extrem- und Wendestellen sollen per Schieberegler auf drei Stellen genau eingestellt werden. Das Ergebnis 3 1,732...
wird als 1,73 akzeptiert, während 1,74 ohne Hinweis auf eventuelle Rundungsfehler als falsch gilt. Beim Bereich Textverständnis geht es oft entweder um die Auswahl von einem von immerhin drei Formelpaaren für Nebenbedingung und
Zielfunktion zu einer Extremwert-Aufgabenstellung. Oder man muss aus mehreren Formeln die auszuwählen, die den
vorgestellten Text am besten wiedergibt bzw. -- anders herum -- man muss zu einer genannten Formel das Teilstück in
einer längeren Textpassage markieren, das den entsprechenden mathematischen Zusammenhang beschreibt (wird allerdings ein Randwort nicht mit markiert, wird eine sonst richtige Antwort nicht anerkannt -- auch hier zeigen sich grundsätzliche Beschränkungen der Maschine). Aber überhaupt Übungen dieser Art softwaremäßig umzusetzen ist jedenfalls
sehr verdienstvoll, wissen wir doch alle, wie schwer sich Schülerinnen und Schüler mit Problemen dieser Art tun und wie nötig solche Übungen sind.
Unter Wissensstand kann eine Statistik abgerufen werden, mit welchem Erfolg die Übungsbeispiele aus den verschiedenen Bereichen bearbeitet wurden.
Glanzstück der CD sind aber sicher die drei Projekte:
Im Projekt „Autobahnbaustelle" geht es letztlich darum, die Geschwindigkeit zu finden, bei der der Verkehrsdurchsatz auf einer
einspurigen Straße am größten ist. Filme regen zur Verkehrszählung und Durchsatzschätzung an, die Modellbildung erfolgt
transparent, wobei Vereinfachungsschritte klar festgehalten (und auch später hinsichtlich ihrer Auswirkungen untersucht)
werden. Gerade diese Projekte lohnen den Kauf der CD -- wobei ich hier allerdings weniger an Nachhilfe denke, sondern auch daran, diese CD z.B. Schülerinnen oder Schülern in die Hand zu drücken, damit sie ein Referat oder vielleicht sogar eine Facharbeit zu einem vorgestellten (oder besser noch: ähnlichen) Thema anfertigen. Vielen Lehrerinnen und Lehrer, die vor der unterrichtlichen Umsetzung von MUED-Ideen bisher zurückgeschreckt sind, mag der Mathe Tutor auch als willkommene eigene Anleitung dienen (mehr zur MUED auf meiner Mathematik-Hauptseite). Und zum Umlauf in der Fachkonferenz ist die Software allemal geeignet.
Ob die Erwartung, dass gerade die von der Werbung angesprochenen leistungsschwächeren Schüler vom innovativen Ansatz profitieren (zumal sie ja mehr lernen müssen, als im herkömmlichen Unterricht verlangt), mag dahingestellt bleiben. Auch halte ich es nicht für realistisch, dass Schülerinnen und Schüler vor dem Anklicken der Lösung immer erst selber überlegen oder rechnen -- ein Manko, mit dem natürlich jedes Software-Produkt leben muss (nur die Termeingabe von „Mathematik interaktiv / Telekolleg" ist besser, weil nicht einfach geklickt werden kann). Aber für die von mir bezeichnete Zielgruppe und für alle, die einige Projekte einmal elektronisch präsentiert sehen oder präsentieren möchten, ist diese Software zu empfehlen -- zumal es sie wegen der nachdrängenden Neuauflage jetzt sehr günstig gibt.
Dabei soll nicht verschwiegen werden, dass die Computerprogrammierung beim „Mathe Tutor" von allen hier besprochenen Programmen am schlechtesten ist: Die Navigation zwischen den Seiten ist bisweilen schwierig, weil die hierarchische Struktur unklar ist. Bei höheren Bildschirmauflösungen beschränkt sich auch dieses Programm auf einen 640x480-Bereich in der Bildmitte. Und meine Version konnte nicht normal beendet werden: Das Programm hing sich regelmäßig beim Schlussbild auf und musste über den Taskmanager abgebrochen werden. Bei böswilligen Fehleingaben ließen sich auch zwischendrin Abstürze provozieren. Für den Start von CD werden zusätzlich noch ca. 10 MB Festplattenspeicher benötigt, weitere Produkte aus der gleichen Reihe (z.B. der Mathe Tutor Geometrie) installieren einige gleiche Dateien noch mal in neue Verzeichnisse.
Für eine neue Version wünsche ich mir, dass noch mehr Interaktivität möglich wird und eine abgestufte Bewertung von Lösungen erfolgt. Freie Eingaben statt Auswahl wären zu wünschen. Und der Multimedia-Einsatz sollte sich weniger nach den Möglichkeiten, als nach den Erfordernissen richten: Ein rotierendes 3D-Modell mag optisch ansprechend und anschaulich sein, ist aber als Lösung eher störend, wenn vom Schüler eine Skizze verlangt wurde. Und ob Realismus und Alltagsnähe dadurch erzeugt wird, dass wir im Film minutenlang mit ansehen müssen, wie sich jemand mit dem Giebel einer Milchtüte abquält, bevor er deren Inhalt in einen Messbecher ausgießen kann, mag unterschiedlich beurteilt werden -- beim realen Experiment im Unterricht hätte man allerdings auch mit solchen Tücken zu kämpfen und entsprechende Wartezeiten..
Im Jan./Februar 2000 nur noch 3,33 DM (bzw. mit drei weiteren Programmen im Restposten-Aktions-Paket für zusammen 9,99 DM + Versand) bei SMM (Best.-Nr. 8325-185).
zum Seitenanfang / zum Seitenende
Mathe Tutor Oberstufe 2.0 (© Maaß/Stöckl, 1999; ISBN 3-901678-04-1, im Vertrieb von Koch Media. UVP knapp 50,- DM.)
Mit dieser Ende '99 erschienen CD liegt die erweiterte Neuauflage des vorstehend besprochenen Mathe-Tutors für die SII vor, der motivierende, multimediale Übung und Nachhilfe am heimischen Computer (mit Windows 95 oder 98) verspricht.
Das lobenswerte Konzept, Schülerinnen und Schülern auch Textaufgaben, Modellbildung und realitätsnahe Projekte näher zu bringen, wurde noch ausgebaut. Die bei der alten Version kritisierte Benutzerführung ist jetzt gut gelungen. In einem schmalen Fenster sieht man links auf dem Bildschirm immer auch eine Gliederung mit den Abschnittsüberschriften des aktiven Kapitels; anhand der Nummern und Zwischenüberschriften im Text (leider nicht durch farbige Unterlegung des gerade bearbeiteten Gliederungspunktes in der Übersicht) gelingt die Orientierung. Bei der Installation werden satte 105 MB auf der Festplatte belegt (während Version 1 noch mit 10 MB aus kam), zusätzlich wird die CD benötigt. Jetzt wird nur die Bildschirmauflösung 800x600 unterstützt (Version 1: nur 640x480).
Das Startmenü bietet die drei großen Bereiche „Lernmodule", „Übungsbeispiele" und „Projekte" -- sowie die Erläuterung der jetzt guten Navigationsmöglichkeiten.
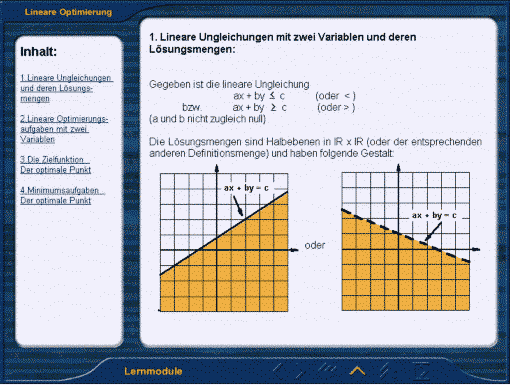Die „Lernmodule" beinhalten Kapitel zu Modellbildung, Textverständnis, elementarer Geometrie (Drei- und
Vierecke, Kreis, Quader, Zylinder, Kegel u. Kugel), *Vektorrechnung, Gleichungen lösen (allgemein, linear,
quadrat., lineare 2x2-Systeme), Intervallschachtelung, *Linearer Optimierung, Funktionsgraphen (lin., quadrat., einige einfache rationale, Wurzel, exp und ln), Trigonometrie, Differentialrechnung, Kurvendiskussion,
Extremwertaufgaben und Integralrechnung. Die mit * gekennzeichneten Kapitel sind neu in der Version 2.0,
andere wurden z.T. erweitert. Angesprochen werden also Themen der Analysis, der (vor allem elementaren)
Geometrie und der Linearen Algebra; Stochastik fehlt leider nach wie vor völlig. In den Lernmodulen sollen
wohl die Grundfertigkeiten der genannten Gebiete wiederholt und gefestigt werden. Meist wird Lehrtext mit
vorgerechneten Beispielen präsentiert, der mit Bildern, gelegentlicher Sprachausgabe oder Videosequenzen
aufgelockert ist. Nur in wenigen „Lernmodul"-Kapiteln wie z.B. bei den Funktionsgraphen oder Gleichungen
sind Eingaben gefordert oder möglich, wobei Koeffizienten verändert werden können oder Lösungen vom
Benutzer verlangt werden -- für mehr Interaktion gibt es dann den Bereich „Übungsbeispiele".
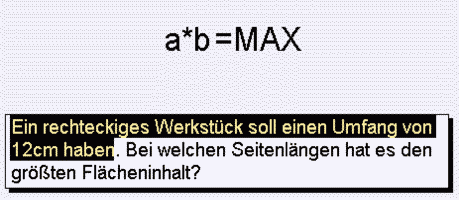„Übungsbeispiele" werden zu den Kapiteln
Differenzieren (unterteilt nach 5
Funktionsklassen), Textverständnis,
*Umfang-, Flächen- und Volumenformeln,
Extremwertaufgaben, Kurvendiskussion, Integration, Funktionen (i.w. Kurvendiskussion), Gleichungen, *Linearem Optimieren, (*)Trigonometrie und Vektorrechnung/Analytischer Geometrie angeboten. Während z.B. beim Differenzieren jeweils drei Aufgaben des gewählten Funktionstyps immer wieder neu
zufällig erstellt und ihre Ableitungen durch Auswahl aus jeweils vier Möglichkeiten gefunden werden müssen, gibt
es bei manchen anderen Kapiteln, wie z.B. den Extremwertaufgaben, nur drei feste Aufgaben, deren Lösungen bei
wiederholter Benutzung eben schon bekannt sind. Beim Textverständnis müssen zu vorgegebenen Formeln gehörige Textpassagen markiert oder umgekehrt unter mehreren
Gleichungen die den Text am besten formalisierende ausgesucht werden. Hier stehen zehn feste Übungen zur Verfügung. Richtige Lösungen werden -- durch das laute „Juchhu" der
Version 1 genervte Mitbewohner atmen auf -- stumm per Text bestätigt: „Diese Antwort ist richtig!". Falsche Lösungsauswahl wird meist mit einem Hinweis auf den gemachten
Fehler kommentiert; außerdem wird automatisch die richtige Antwort gezeigt, was weiteres (Herum-)Probieren unmöglich macht. Die Übungen entsprechen im Stil meist üblichen
Mathematik-Unterrichts- bzw. -Buch-Aufgaben und sind okay; nur in einer Übung zur Vektorrechnung besteht das Programm wegen eines Vorzeichenfehlers beim Vergleich der
Lage zweier Geraden darauf, dass die Richtungsvektoren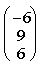 
und 
parallel sind (mit Faktor -3). Der Lösungserfolg wird in der Kapitel-Übersicht mit drei Farben angezeigt.
Im Projekt „Altmetall" wird nach Möglichkeiten gesucht, Blech bei der Herstellung von Konservendosen sparsam einzusetzen. Es werden -- soweit möglich im Dialog -- und von Videosequenzen u.a. zum Dosenöffnen und Messen unterstützt, schrittweise verfeinerte Modelle entwickelt und diskutiert, den tatsächlichen Materialverbrauch zu erfassen und schließlich zu minimieren. Im Projekt „Autobahnbaustelle" wird letztlich die Geschwindigkeit gesucht, bei der die Verkehrsstärke auf einer einspurigen Straße am größten ist. Filme regen zur Verkehrszählung und Durchsatzschätzung an, die Modellbildung erfolgt transparent, wobei Vereinfachungsschritte klar festgehalten (und auch später hinsichtlich ihrer Auswirkungen untersucht) werden. Und im letzten Projekt, der „Milchverpackung", geht es um die materialsparende Produktion von Milchtüten (wie in der ersten Version, s.o.).
Insgesamt ist der Mathe Tutor Oberstufe 2.0 ein durchaus gelungenes Programm, das gegenüber der davor besprochenen Version 1 noch verbessert wurde -- wenngleich auch nicht alle oben geäußerten Wünsche verwirklicht wurden.