| www.r-krell.de |
| Webangebot für Schule und Unterricht, Software, Fotovoltaik und
mehr |
Willkommen/Übersicht > Informatik > Informatik mit Java, Seite t)
Informatik mit Java
Teil t): Simulation einer Turing-Maschine in/mit Java
Das Projekt, eine Turing-Maschine in Java zu programmieren, wird im Folgenden hier - und nach und nach auf weiteren Seiten - ausführlich
vorgestellt. Dabei werden die Entwurfsentscheidungen aufgezeigt, alternative Möglichkeiten angesprochen und der Weg bis zum fertigen Programm
nachvollziehbar und mit Java-Quelltext dargestellt. Bevor man aber eine Turingmaschine programmieren kann, muss man erstmal wissen, was eine
Turingmaschine ist und wie sie funktioniert.
Projekt: Entwicklung einer Turing-Maschinen-Simulation
Eine vollständige Übersicht aller "Informatik mit Java"-Seiten gibt's auf der Informatik-Hauptseite.
Viele der dort aufgeführten Seiten enthalten ausführlich beschriebene Java-Programme im Quelltext. Außerdem wird auf die Seiten
SWE1 und SWE2 zum Software-Engineering hingewiesen.
zum Seitenanfang / zum
Seitenende
Was ist eine Turing-Maschine?
Das Konzept der später nach ihm benannten Turing-Maschine(n) wurde um 1936 von Alan Turing (GB, 1912 - 1954) entwickelt, um im
Gedankenexperiment zu überlegen, welche Aufgaben und Probleme überhaupt von (solchen) Maschinen gelöst werden könnten. Damit
wurde die Theorie der (automatischen) Berechenbarkeit begründet, bevor es die ersten "richtigen" elektrischen bzw. elektronischen Computer
gab.
a) Anschauliche Beschreibung
Turingmaschinen sind einfach aufgebaut: Als (Daten-)Speicher sowie gleichzeitig als Ein- und Ausgabegerät steht nur ein einziges langes
Band zur Verfügung, auf dem in linear nebeneinander angeordneten Feldern jeweils einzelne Zeichen stehen können. Alle übrigen Felder
des Bandes sind leer. Über dem Band bewegt sich ein kombinierter Lese- und Schreibkopf, der jeweils genau ein Zeichen lesen und es eventuell
durch ein anderes Zeichen ersetzen kann. Der Einfachheit halber lässt man dabei den Kopf immer ein Zeichen schreiben: soll das
ursprünglich gelesene Zeichen erhalten bleiben, wird es mit sich selbst überschrieben, sonst schreibt man ein anderes Zeichen aufs Band.
Nach der Lese- und Schreib-Operation kann der Kopf über der gleichen Stelle des Bandes verharren (und im nächsten Arbeitsschritt das
gerade ins aktuelle Band-Arbeitsfeld geschriebene Zeichen wieder lesen) oder sich auf dem Band entweder um eine Stelle nach links oder um eine
Stelle nach rechts bewegen, um im nächsten Takt den Inhalt des Nachbarfelds zu lesen und ggf. zu verändern.
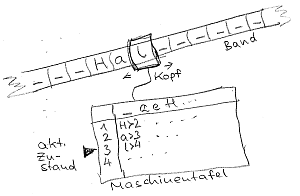 Die Aktionen des
Lese-/Schreib-Kopfes werden durch das Programm gesteuert, das bei einer begrenzten Zahl möglicher Zustände durch die so genannte
Maschinentafel festgelegt wird. Die Maschinentafel ist eine zweidimensionalen Tabelle, in der für jeden Zustand und jedes gerade vom Band
gelesene Zeichen eingetragen ist, wie die Maschine reagieren soll: welches Zeichen aufs Band geschrieben wird, ob bzw. in welche Richtung sich der
Kopf bewegen soll, und welchen (Folge-)Zustand die Maschine annimmt, bevor der nächste Arbeitstakt beginnt. Die Maschinentafel kann
während des Programmablaufs nicht mehr verändert werden.
Die Aktionen des
Lese-/Schreib-Kopfes werden durch das Programm gesteuert, das bei einer begrenzten Zahl möglicher Zustände durch die so genannte
Maschinentafel festgelegt wird. Die Maschinentafel ist eine zweidimensionalen Tabelle, in der für jeden Zustand und jedes gerade vom Band
gelesene Zeichen eingetragen ist, wie die Maschine reagieren soll: welches Zeichen aufs Band geschrieben wird, ob bzw. in welche Richtung sich der
Kopf bewegen soll, und welchen (Folge-)Zustand die Maschine annimmt, bevor der nächste Arbeitstakt beginnt. Die Maschinentafel kann
während des Programmablaufs nicht mehr verändert werden.
Während das Band theoretisch unendlich lang sein kann, dürfen nur endlich viele verschiedene Zeichen benutzt werden (die das so
genannte Bandalphabet bilden) und sind auch nur endlich viele Zustände erlaubt. Zum Bandalphabet gehört auch das Leerzeichen, das sich
anfangs in allen nicht anderweitig beschrifteten Feldern des Bandes befindet. Zu den Zuständen gehört mindestens ein Endzustand, bei
dessen Erreichen die Maschine anhält und so den ordnungsgemäßen Abschluss des Programms anzeigt. Allerdings gibt es durchaus
Aufgabenstellungen, für die kein Turing-Programm möglich oder bekannt ist, das sicher irgendwann anhält (Halteproblem).
Interessanterweise können die hier beschriebenen Turingmaschinen (wobei man eine Turingmaschine mit anderem Programm als eigene
Turingmaschine auffasst) genau die gleichen Probleme lösen und Aufgaben berechnen wie unsere heutigen, modernsten Computer [mehr dazu am Ende
des Abschnitts b3) weiter unten!]. Deshalb gehören Turingmaschinen nach wie vor zum wichtigen Inventar der Theoretischen Informatik und werden
dort auch heute noch gerne als Computermodelle verwendet.
zum Seitenanfang / zum Seitenende
b) Einige Turing-Maschinen-Beispiele
b1) "Hallo Welt"
Wenn Turingmaschinen genauso mächtig sind wie normale Computer, dann muss es auch eine Turingmaschine geben, die "Hallo Welt" auf das
anfangs leere Band schreibt. Das Bandalphabet hierfür besteht außer dem Leerzeichen _ aus den sechs Buchstaben des zu schreibenden
Textes, also aus { _, a, e, H, l, o, t, W }. Ein schnell geschriebenes Programm benutzt elf Zustände und startet im Zustand 1. Die
Maschinentafel wäre damit eine (8 x 11)-Tabelle plus Randbeschriftung, wobei hier allerdings nur die erste innere Spalte (unter dem
Leerzeichen _ ) interessant ist, weil das Band anfangs leer ist und der Kopf nur nach rechts wandert, sodass nie andere Zeichen als das Leerzeichen
gelesen werden. Jeder Tabelleneintrag besteht aus einem Tripel: (neues Zeichen, Kopfbewegung, nächster Zustand). So bedeutet etwa das Tripel
(H,>,2) bzw. kurz H>2, dass das Zeichen H aufs Band geschrieben wird, der Kopf sich dann um ein Feld nach rechts
(>) bewegt und die Maschine in den Zustand 2 übergeht:
| Maschinentafel einer Turingmaschine, die "Hallo Welt" auf ein anfangs leeres Band schreibt und hält |
| letzter Zustand \ gelesenes Zeichen |
_ |
a |
e |
H |
l |
o |
t |
W |
| 1 (Startzustand) |
H>2 |
|
|
|
|
|
|
|
| 2 |
a>3 |
|
|
|
|
|
|
|
| 3 |
l>4 |
|
|
|
|
|
|
|
| 4 |
l>5 |
|
|
|
|
|
|
|
| 5 |
o>6 |
|
|
|
|
|
|
|
| 6 |
_>7 |
|
|
|
|
|
|
|
| 7 |
W>8 |
|
|
|
|
|
|
|
| 8 |
e>9 |
|
|
|
|
|
|
|
| 9 |
l>10 |
|
|
|
|
|
|
|
| 10 |
t>11 |
|
|
|
|
|
|
|
| 11 (Endzustand) |
Halt |
Halt |
Halt |
Halt |
Halt |
Halt |
Halt |
Halt |
Es ist sofort klar, dass die Maschine - irgendwo auf einem völlig leeren Band im Zustand 1 gestartet - wirklich die gestellte Aufgabe
löst, nämlich in 10 Schritten insgesamt "Hallo Welt" notiert und mit dem Kopf hinter dem letzten Buchstaben t stehen bleibt. Das Anhalten
signalisiert den Erfolg und das fehlerfreie Programmende. Da beim anfangs leeren Band nie andere Zeichen als das Leerzeichen _ gelesen werden
können, brauchen hier die meisten Spalten der Tabelle gar nicht ausgefüllt werden (oder könnten beliebige Inhalte haben).
Muss man hingegen befürchten, dass auf dem Band schon irrtümlich etwas steht und will diesen Fall als Fehler kennzeichnen, könnte
man in alle bisher frei gelassenen Tabellenfelder Einträge schreiben, die z.B. das gelesene falsche Zeichen mit sich selbst
überschreiben, den Kopf an der Stelle lassen und auch im gleichen Zustand bleiben, sodass das falsche Zeichen endlos immer wieder gelesen und
geschrieben wird, die Maschine also nie anhält -- Im folgenden Abschnitt b2) wird auch noch eine andere Art der Fehlerbehandlung gezeigt.
zum Seitenanfang / zum Seitenende
b2) Addition von zwei (Dual-)Zahlen
Das vorige Beispiel erscheint - nachdem man mal die Arbeitsweise einer Turingmaschine erfasst hat - nicht sehr kompliziert. Kann aber eine
Turingmaschine außer dieser Primitivform von Textverarbeitung auch rechnen? Dass soll beispielhaft an der Addition zweier einstelliger
Dualzahlen x und y, gezeigt werden - wenn x und y Bits, nämlich Elemente aus {0,1} sind.
Die Turingmaschine soll auf alle richtig gestellten Aufgaben der Form "x+y=" die korrekte Summe rechts neben das Gleichheitszeichen schreiben und
dann anhalten. Die Aufgabe muss vor dem Start bereits auf dem Band stehen (als anfängliche Bandinschrift), der Kopf soll sich anfangs auf dem
ersten Zeichen der Aufgabe befinden (also auf/über dem x).
Startzustand sei immer der Zustand 1.
Die Turingmaschine mit folgender Maschinentafel ist geeignet:
| Turingmaschine, die hinter die anfängliche Bandinschrift "x+y=" die Summe schreibt und hält |
| letzter Zustand \ gelesenes Zeichen |
_ |
+ |
= |
0 |
1 |
| 1 (Start auf x) |
_=13 |
+=13 |
==13 |
0>2 |
1>3 |
| 2 |
_=13 |
+>4 |
==13 |
0=13 |
1=13 |
| 3 |
_=13 |
+>5 |
==13 |
0=13 |
1=13 |
| 4 |
_=13 |
+=13 |
==13 |
0>6 |
1>7 |
| 5 |
_=13 |
+=13 |
==13 |
0>7 |
1>8 |
| 6 |
_=13 |
+=13 |
=>9 |
0=13 |
1=13 |
| 7 |
_=13 |
+=13 |
=>10 |
0=13 |
1=13 |
| 8 |
_=13 |
+=13 |
=>11 |
0=13 |
1=13 |
| 9 |
0>14 |
+=13 |
==13 |
0=13 |
1=13 |
| 10 |
1>14 |
+=13 |
==13 |
0=13 |
1=13 |
| 11 |
1>12 |
+=13 |
==13 |
0=13 |
1=13 |
| 12 |
0>14 |
+=13 |
==13 |
0=13 |
1=13 |
| 13 (Dauerzustand nach Eingabefehler) |
_=13 |
+=13 |
==13 |
0=13 |
1=13 |
| 14 (Endzustand) |
Halt |
Halt |
Halt |
Halt |
Halt |
Dabei ist zu beachten, dass diese Maschine nicht nur addiert, sondern auch die Eingabe auf syntaktische Korrektheit überprüft. Steht
der Kopf anfangs nicht auf dem ersten Bit oder gibt es zusätzliche Leerzeichen, mehrstellige Dualzahlen oder fehlende Rechen- oder
Gleichheitszeichen bzw. steht direkt hinter dem Gleichheitszeichen schon eine Zahl auf dem Band, dann gerät die Maschine in den Zustand 13 und
hält nie an: der Kopf bleibt über dem beanstandeten Zeichen und liest und schreibt dies endlos immer wieder! Zur besseren Übersicht
wurden die Einträge, die der Fehlerbehandlung dienen, in der Tafel kursiv und hellgrau eingetragen.
Bei richtiger Eingabe schreibt die Maschine die richtige ein- oder zweistellige Summe und hält an, wobei dann der Kopf hinter der letzten
geschriebenen Ziffer steht.
Die abgebildete Maschine merkt sich übrigens in den Zuständen, welcher Teil der Eingabe bereits gelesen wurde: Wurde als Eingabeanfang
bzw. Beginn der Aufgabe "0" erkannt, führt das zum Zustand 2. Der Eingabeteil "0+" führt zum Zustand 4, "0+0" zum Zustand 6, "0+0=" zum
Zustand 9, der schließlich dafür sorgt, dass das anschließende Leerzeichen mit dem Ergebnis 0 überschrieben wird (jetzt also
"0+0=0" auf dem Band steht und der Kopf nach rechts dahinter rückt), bevor die Maschine anhält.
In ähnlicher Weise führt die Erkenntnis von "1" zum Zustand 3, "1+" zum Zustand 5, "1+0" zum Zustand 7, "1+0=" zum Zustand 10, sodass nun
das Ergebnis 1 geschrieben werden kann und muss. Umgekehrt ist bei Erreichen beispielsweise des Zustands 7 sicher, dass entweder bereits "1+0" oder
"0+1" gelesen wurde, das spätere Ergebnis also 1 sein muss, aber zunächst das Gleichheitszeichen erwartet wird, bevor das Ergebnis (nach
Erreichen von Zustand 10) geschrieben werden darf.
Dass wirklich "0+1=" (Zustand 10) und auch "1+1=" (Zustand 11) schrittweise richtig erkannt werden, mag an der obigen Tabelle als Übung
überprüft werden. Außerdem ist erkennbar, dass im letzten Fall das zweistellige Ergebnis 10 notiert wird, wobei der Zustand 12
'weiß', das bereits die vordere der beiden Ergebnisziffern (mit dem Stellenwert 2) geschrieben wurde und nur noch die Einerziffer 0 fehlt,
die jetzt an die leere Stelle muss.
Allgemein ist eine Turingmaschine allerdings nicht darauf angewiesen, sich Fortschritte oder Zwischenergebnisse unbedingt in Zuständen zu
merken, da auch das Band z.B. zum Notieren von Zwischenwerten benutzt werden kann. Spezielle Codes, die über Buchstaben hinausgehen, die
für die Aufgabe bzw. die Bandinschrift verwendet werden, können Zustände sparen: So kann etwa ein Zwischenergebnis Zehn statt
dezimal (d.h. als eine 10 aus zwei Zeichen 1 und 0) besser in einem Zeichen, etwa als A notiert werden; ein eingefügtes, vielleicht am Ende
wieder zu entfernendes Zeichen $ könnte markieren, wie weit eine Aufgabe bereits bearbeitet wurde.
Dadurch, dass die oben vorgestellte Maschine praktisch Scanner und Parser vereint, die ursprünglich auf dem Band
befindliche Aufgabe also auf richtige Schreibweise kontrolliert und dann korrekt löst, ist die Maschine relativ aufwändig. Vertraut man
auf die korrekte Eingabe der beiden jetzt nur noch durch genau ein Leerzeichen getrennten Summanden x und y und verzichtet auf Rechen- und
Gleichheitszeichen, reicht eine viel kleinere Maschine zum Ersetzen der Summanden durch ihre Summe (wobei beim Halt also nur noch die Summe auf den
Band steht, während die ursprünglichen Summanden gelöscht wurden oder überschrieben sind):
| Turingmaschine, die die Bandinschrift "x y" durch ihre Summe ersetzt |
| letzter Zustand \ gelesenes Zeichen |
_ |
0 |
1 |
| 1 (Start auf x) |
_=1 |
_>2 |
_>3 |
| 2 |
_>2 |
0>5 |
1>5 |
| 3 |
_>3 |
1>5 |
1>4 |
| 4 |
0>5 |
0=4 |
1=4 |
| 5 (Endzustand) |
Halt |
Halt |
Halt |
Die hellgrauen Einträge kommen nur bei fehlerhafter Bandbeschriftung zum Einsatz (wenn neben bzw. hinter dem y noch etwas steht), sollten
also laut Voraussetzung nie gebraucht werden und führen dazu, dass die Maschine im Fehlerfall endlos an der Fehlerstelle verharrt, aber nicht
anhält (ein eigener Fehlerzustand, wie oben als Zustand 13 eingefügt, ist also gar nicht nötig - vgl. auch Text am Ende von
b1)).
Diese Additionsmaschine mit 5 Zuständen ist übrigens die Turingmaschine, die auf der nächsten
Projekt-Webseite als Beispiel zum Speichern auf einem dauerhaften Speichermedium bzw. Datenträger verwendet wird.
zum Seitenanfang / zum Seitenende
b3) Turingmaschinen für logische Verknüpfungen
In ähnlicher Weise wie die in b2) vorgestellten Additionsmaschine können Turingmaschinen geplant werden, die
- ein anfangs auf dem Band befindliches Bit invertieren. Die Version mit Parser, die hinter die Aufgabe "~0=" bzw. "~1=" die richtige Negation
schreibt, ist nicht schwer. Noch schneller ist die Einfachversion programmiert, die x durch ~x ersetzt, also aus einer 0 eine 1 macht und
umgekehrt:
| Turingmaschine, die die Bandinschrift "x" durch ihr Inverses ersetzt |
| letzter Zustand \ gelesenes Zeichen |
_ |
0 |
1 |
| 1 (Start auf x) |
_=1 |
1>2 |
0>2 |
| 2 (Endzustand) |
Halt |
Halt |
Halt |
- ein logisches Und simulieren, d.h. die Bandinschriften wie etwa "1&0=" richtig durch 0 vervollständigen bzw. - weniger mühsam -
zwei Bits auf dem Band durch das Resultat ihrer Und-Verknüpfung ersetzen.
- eine logische Oder-Verknüpfung für zwei Bits x und y durchführen bzw. hinter Aufgaben vom Typ "x | y=" das richtige Ergebnis
der Disjunktion schreiben.
Hier wurden die logischen Verknüpfungen in der Javasyntax aufgeschrieben; man muss lediglich das Operator-Zeichen austauschen, um mit der
sonst gleichen Maschine die mathematische Notation (etwa mit 'dach' statt &) verarbeiten zu können.
Mit der Addition und den drei logischen Operationen beherrschen Turingmaschinen die Grundfunktionen einer Arithmetisch-Logischen-Einheit (ALU),
die den Kern des Rechenwerks jedes modernen Computers bildet (vgl. auch mein im pdf-Format verfügbares Skript über Logik und Aufbau eines
Computers, gepackt in voramor-pascal.zip bzw. voramor-java.zip auf meiner Software-Seite). Wenn aber Turingmaschinen die Grundoperationen eines normalen Computers beherrschen, können sie im Prinzip
auch alles berechnen, was ein normaler Computer (also eine von-Neumann-Registermaschine) berechnen kann. Das führt zur Erkenntnis 1:
Turingmaschinen sind mindestens so leistungsfähig wie normale Computer!
Da umgekehrt Turingmaschinen auf Digital-Computern simuliert werden können - das hier beschriebene und im Folgenden ausgeführte Projekt
widmet sich genau dieser Aufgabe - sind normale Computer offensichtlich mindestens so mächtig wie Turingmaschinen, da sie Turingmaschinen
simulieren können (aber auch noch andere Programme laufen). Daraus ergibt sich Erkenntnis 2: Normale Computer können mindestens so viel
wie Turingmaschinen.
Aus beiden Erkenntnissen zusammen ergibt sich die eingangs (am Ende von Abschnitt a)) getroffene Aussage, dass moderne Computer und die 1936
modellhaft erdachten Turingmaschinen prinzipiell gleichwertig sein müssen, weil keine der beiden Geräteklassen mehr Aufgaben lösen
kann.
zum Seitenanfang / zum Seitenende
c) Theoretische Beschreibung
Wie oben am Ende des Abschnitts a) bereits erwähnt, werden Turingmaschinen gerne in der Theoretischen Informatik verwendet. Dort gibt man
sich aber nicht mit einer anschaulichen Beschreibung und Beispielen zufrieden, sondern definiert formal, was eine Turingmaschine ist. Dabei findet
man unterschiedliche Definitionen: manchmal wird nicht nur ein Endzustand, sondern werden mehrere Endzustände zugelassen; an anderer Stelle
wird zwischen dem Eingabealphabet (das nur die in der anfänglichen Bandinschrift verwendeten Zeichen enthält) und dem umfassenderen
Bandalphabet aller möglichen, auch später zu schreibenden Zeichen unterschieden, wobei dann meist das Leerzeichen nicht zum
Eingabealphabet gehört - obwohl die Bandinschrift trotzdem aus mehreren, durch Leerzeichen getrennten Teilen bestehen darf. Wird die
Kopfbewegung mit Buchstaben wie L (links), R (rechts) und S (still stehen bleiben) abgekürzt, dürfen diese Buchstaben in einigen
Definitionen nicht im Eingabe- oder Bandalphabet vorkommen, offenbar um Verwechslungen zu vermeiden [obwohl diese durch die Position im
Tabelleneintrag eigentlich ausgeschlossen sein sollten: bei ==13 bzw. (=, =, 13) in meiner
ersten Maschinentafel in b1) ist das erste Zeichen des Tripels das neu aufs Band zu schreibende Zeichen des Bandalphabets (hier das
Gleichheitszeichen), in der Mitte gefolgt vom Zeichen für die Kopfbewegung (wobei ich mit = den Stillstand symbolisiere) und an letzter Stelle
gefolgt von der Nummer des Zustands. Eine einstelligen Zustandsnummer könnte ohne Beachtung der allerdings wichtigen Reihenfolge ja auch mit
einem Zeichen des Bandalphabets verwechselt werden, wie der Eintrag 1>2 in meiner Maschinentafel in b3) zeigt: die erste 1 ist das aufs
Band zu schreibende Zeichen, die hintere 2 die Nummer des Folgezustands]. Manche Autoren verzichten auch auf die von mir oben jeweils angegebene
letzte Zeile in der Maschinentafel, die ja nur 'Halt' enthält, und zählen den Endzustand deshalb bei den Zuständen nicht mit,
würden also die Invertier-Maschine aus b3) als Turingmaschine mit nur einem Zustand bezeichnen. Im Zug weiterer Verwirrung erlauben manche
Definitionen nur ein einseitig unbeschränktes Band (Strahl) statt eines nach beiden Seiten unendlichen Bandes oder erlauben keinen Stillstand
des Lese-/Schreib-Kopfes. Zum Glück haben solche scheinbaren Einschränkungen keine Auswirkung auf das, was mit solchen Maschinen
berechnet werden kann. Eventuell sind die Programme etwas aufwändiger (oder bei mehreren Endzuständen vielleicht auch kürzer), aber
im Endeffekt können letztlich immer genau die gleichen Probleme berechnet werden wie mit einer Maschine mit beidseitig offenem Band, drei
Kopf-'bewegungs'-möglichkeiten und nur genau einem Endzustand. Ich definiere eine Turingmaschine M durch ein 6-Tupel:
M = (B, Z, bLeer, d,
zS, zE,)
d.h. eine Turingmaschine M braucht
- ein endliches Bandalphabet B mit allen möglichen Zeichen, die vom Band gelesen oder aufs Band geschrieben werden
können, einschließlich des
- Leerzeichens bLeer, das insofern eine Sonderrolle spielt, weil es - abgesehen von der endlichen Bandinschrift
i - sonst überall auf dem Band ist. (In meinen Beispielen oben habe ich immer den Unterstrich _ als Leerzeichen benutzt.)
- einer endlichen Menge Z von Zuständen einschließlich
- einem Anfangs- oder Startzustand zS (in meinem Beispielen immer Zustand 1) sowie
- einem (einzigen) Endzustand zE, bei dessen Erreichen die Turingmaschine anhält (bei mir immer der
Zustand mit der höchsten Nummer).
- die Überführungsfunktion d: B×Z° ---> B × {<,=,>} × Z, die jeder möglichen
Kombination (Paar) aus gelesenem Zeichen balt aus B und aktuellem Zustand zalt aus Z° ein Tripel aus einem neuem
Bandzeichen bneu aus B, einer Kopfbewegung k aus {<,=,>} und einem Folgezustand zneu aus Z zuordnet: d:
(balt, zalt) |---> (bneu, k, zneu ). Dabei muss Z° =
Z \ {zE} definiert werden, weil zum Endzustand zE ja kein richtiger Eintrag mehr gehört, sondern die
Maschine nur noch hält. Die Übergangsfunktion d wird meist durch eine vollständige Wertetabelle in Form der Maschinentafel
definiert; gelegentlich findet man aber auch andere Darstellungen (etwa ähnlich den Automatengraphen).
Es fehlt noch
- die Bandinschrift i, die schon vor dem Start der Maschine auf dem Band steht. Im Allgemeinen gilt i nicht als Teil der Turingmaschine (und
fehlt daher oben im 6-Tupel), sondern i ist eine mögliche Eingabe. Man wendet also die Maschine M auf die Bandinschrift i an. Damit man
(zusätzlich zum für alle Inschriften i immer gleichen Startzustand zS) nicht auch noch die Position des Kopfes beim Start
relativ zu i angeben muss, wird vereinbart, dass der Kopf anfangs immer auf dem ersten 'echten' Zeichen der Bandinschrift stehen soll. Nur bei
leerer (nicht vorhandener) Bandinschrift i startet die Maschine auf einem Leerzeichen, also irgendwo mitten auf dem Band. Die Bandinschrift i
darf nur aus endlich vielen Zeichen bestehen, von denen natürlich jedes aus dem Bandalphabet B kommen muss.
Das Vorhandensein von Band und Kopf wird in der Regel stillschweigend vorausgesetzt und findet sich nicht explizit im 6-Tupel oder in i wieder.
Offensichtlich muss es diese Dinge aber geben, weil sonst B, bLeer oder i sowie die innerhalb von d vorkommenden Kopfbewegungen
{<,=,>} bedeutungslos wären. Die Maschinentafel wird implizit durch d gefordert.
Wie oft in der Informatik ist die formale, algebraisch-"axiomatische" Definition ohne zusätzliche Beschreibung nicht oder nur schwer
verständlich und gibt ohne Weiteres keinen Hinweis auf Aussehen und Funktion des üblichen Turingmaschinen-Modells.
Ein Blick in Lehrbücher der Theoretischen Informatik, in Wikipedia oder ein kurze Internetrecherche werden schnell zu ähnlichen, aber
nicht immer ganz identischen formalen Definition führen, wobei die Komponenten des Tupels gerne mit griechischen Buchstaben bezeichnet werden.
Weiterhin gibt es neben den hier vorgestellten deterministischen Turingmaschinen manchmal auch noch weitere Formen.
zum Seitenanfang / zum Seitenende
d) Ehrgeizige Programmierung und Fleißige Biber (busy beaver)
Während bei Hochsprachenprogrammen (also etwa Java-Programmen) heute ein übersichtlicher, leicht wartbarer, gut-strukturierter und
Objekt-orientierter Programmierstil das Ziel ist (auch wenn der Programmtext dadurch deutlich an Umfang gewinnt), entwickeln
Turing-Maschinen-Ersteller oft den Ehrgeiz, ein Problem mit einer möglichst kleinen Turing-Maschine zu lösen: Die Anzahl der
Zustände soll minimal sein und das Bandalphabet wird auch auf das Nötigste beschränkt und soll möglichst keine bzw.
höchstens wenige zusätzliche Zeichen für Zwischenergebnisse u.ä. enthalten.
Als Königsdiziplin des Minimalismus gilt seit dem Jahr 1962 die Programmierung so genannter Fleißiger Biber. Bei dieser Sonderform
von Turingmaschinen ist das Bandalphabet auf zwei Zeichen, nämlich das Leerzeichen _ und einen Strich | (der als Baumstamm gedeutet werden
kann) beschränkt. Damit der Biber fleißig ist, darf der Kopf nicht still stehen, d.h. es gibt nur die beiden Kopfbewegungen links (<)
oder rechts (>). Ziel ist es, unter diesen Bedingungen mit möglichst wenigen Zuständen möglichst viele Striche lückenlos
nebeneinander auf das anfangs leere Band zu schreiben, bevor der Biber hält.
Das Anhalten ist wichtig, denn eine Maschine mit nur einem einzigen Zustand 1 und dem Tabelleneintrag |>1 in der Leerzeichen-Spalte
dieses Startzustands würde unendliche viele Striche schreiben können, kommt aber nie zum Halt.
Zählt man den Endzustand nicht mit, so kann der beste Fleißige Biber mit genau einem echten Zustand nur einen Strich, ein
Fleißiger Biber mit 2 echten Zuständen schon 4 Striche, ein Biber mit 3 Zuständen insgesamt 6 Striche und ein 4-Zustands-Biber 13
Striche schreiben. Für einen Biber mit 5 echten Zuständen galt bis zum Jahr 1983 ein Rekord von 240 Strichen. Binnen Jahresfrist wurden
Maschinen für 501 und schließlich für 1915 Striche ersonnen und seit dem Jahr 1989 ist ein Biber mit 5 Zuständen bekannt, der
sogar 4098 Striche produziert. Ob noch eine weitere Steigerung der Strichzahl möglich ist, ist unbekannt. Die Anzahl der Striche, die mit 6
echten Zuständen geschrieben werden kann, ist hingegen riesig viel größer: Die seit dem Jahr 2010 erreichbare Anzahl von Strichen
ist eine Dezimalzahl mit 18267 Stellen!
zum Seitenanfang / zum
Seitenende
Projekt: Javaprogramm zur Simulation von Turingmaschinen
Nachdem jetzt bekannt ist, was eine Turingmaschine ist und wie sie funktioniert, kann mit der Programmierung begonnen werden. Zwar können
im Internet ohne Weiteres einige kostenlose Turingmaschinen-Programme gefunden werden, die sich auch für den Schulunterricht oder das
(Selbst-)Studium eignen - auf meiner Software-Seite gibt es mit 'TuringMa 3.0' auch noch ein betagtes, leicht (aber antiquiert) bedienbares, seinerzeit in
Turbo-Pascal programmiertes fertiges eigenes Simulationsprogramm -, soll hier ein neuer Versuch mit Java unternommen werden. Dabei werden die
Entwurfsentscheidungen und Entwicklungsschritte mitgeteilt und erläutert. Dieses schon recht umfangreiche Projekt wird in mehrerer Hinsicht
über bisher Gezeigtes und den normalen Schulunterricht (auch des Informatik-Leistungskurses) hinaus gehen:
Vier Vorhaben
- Die auf meinen vielen Seiten "Informatik mit Java" entwickelten und vorgestellten Programmen haben oft relativ ähnliche
Oberflächen, die den Blick nicht von der eigentlichen Aufgabe ablenken sollten, sondern nur die notwendigen Ein- und Ausgaben
einigermaßen komfortabel ermöglichen sollten.
Aufwändigere Techniken - Menüleisten mit Aufklappmenüs oder Ribbons, aufpoppende Kontextmenüs und Eingabefenster - wurden auf
meiner Webseite noch nicht mit Java vorgeführt, sind hier aber möglicherweise sinnvoll.
- Und nur in wenigen Fällen wurde auch ein Abspeichern oder ein Öffnen bereits gespeicherter Daten programmiert. Nur in der erweiterten Fuhrparkverwaltung, in dort zusätzlich angegebenen
Arbeitsblättern und bei den binären Sortierbäumen wurden mit
aufDisk und vonDisk Methoden zum Speichern oder Öffnen von Dat(ei)en auf der Festplatte, SSD, USB-Stick oder einem anderen
nichtflüchtigen Speicher behandelt.
Zwar verwendet auch meine Compiler-Simulation Datei-Operationen, die allerdings
nicht im Quelltext vorgestellt wurden. Das Java-SQL-Interface greift nur indirekt
über Datenbankbefehle auf periphere Speicher zu, sodass keine Java-Ein-/Ausgabe-Operationen zum Einsatz kommen. Und beim Kartenspiel-Projekt oder den Programmen P9_A3b (Galgenmännchen) bzw. dem Autorennen P12 kann man auch kaum von Dateioperationen sprechen, wenn nur mit
einem einfachen Java-Befehl fertige Bilder in die Oberfläche geladen werden: ein echter Transfer eigener Daten - etwa das Speichern eines
Spielstands oder das Zurückholen eines in einer früheren Sitzung angefangenen Spiels - fehlt. Bei den vielen andere Anwendungen selbst
mit größeren Datenstrukturen (etwa bei den linearen abstrakten Datentypen) habe ich auf Schreiben/Lesen in externe Speicher ganz
verzichtet.
Das soll jetzt anders werden.
- Schließlich kann auch noch überlegt werden, ob ein Ausdruck der Turingmaschine auf Papier wünschenswert wäre - und
welcher Programmieraufwand getrieben werden muss, wenn man nicht einfach auf die "(ganzen) Bildschirm drucken"-Funktion des Betriebssystems
verweisen will, sondern eine eigene Druckfunktion implementieren will.
- Dabei soll natürlich die eigentliche Simulation der Turingmaschine wieder weitgehend unabhängig von der Oberfläche bzw. der
Benutzerschnittstelle in einer eigenen Klasse programmiert werden.
Diese Vorhaben werden ab Sommer 2019 nach und nach realisiert - gehen Sie auf die nächste(n) Seiten(n) und schauen, was schon alles da
ist!
weiter zur zweiten Seite des "Turingmaschinen-Projekts": Speichern und Öffnen von
Turingmaschinen - Untersuchung dreier Varianten
springe direkt zur dritten Seite des "Turingmaschinen-Projekts": Benötigte Eigenschaften und Fähigkeiten im
Hintergrund
zurück zum Anfang der Informatik-Hauptseite
direkt zur Übersicht aller "Informatik-mit-Java"-Seiten auf der
Informatik-Hauptseite
 Die Aktionen des
Lese-/Schreib-Kopfes werden durch das Programm gesteuert, das bei einer begrenzten Zahl möglicher Zustände durch die so genannte
Maschinentafel festgelegt wird. Die Maschinentafel ist eine zweidimensionalen Tabelle, in der für jeden Zustand und jedes gerade vom Band
gelesene Zeichen eingetragen ist, wie die Maschine reagieren soll: welches Zeichen aufs Band geschrieben wird, ob bzw. in welche Richtung sich der
Kopf bewegen soll, und welchen (Folge-)Zustand die Maschine annimmt, bevor der nächste Arbeitstakt beginnt. Die Maschinentafel kann
während des Programmablaufs nicht mehr verändert werden.
Die Aktionen des
Lese-/Schreib-Kopfes werden durch das Programm gesteuert, das bei einer begrenzten Zahl möglicher Zustände durch die so genannte
Maschinentafel festgelegt wird. Die Maschinentafel ist eine zweidimensionalen Tabelle, in der für jeden Zustand und jedes gerade vom Band
gelesene Zeichen eingetragen ist, wie die Maschine reagieren soll: welches Zeichen aufs Band geschrieben wird, ob bzw. in welche Richtung sich der
Kopf bewegen soll, und welchen (Folge-)Zustand die Maschine annimmt, bevor der nächste Arbeitstakt beginnt. Die Maschinentafel kann
während des Programmablaufs nicht mehr verändert werden.