
| www.r-krell.de |
| Webangebot für Schule und Unterricht, Software, Fotovoltaik und mehr |
Willkommen/Übersicht > Informatik >
Teil l): Schutz der Programmieridee durch (Krypto-)Obfuscation
Eine vollständige Übersicht aller meiner Seiten "Informatik mit Java" gibt's auf der Informatik-Hauptseite!
Diese Seite l) "Schutz der Programmieridee durch
(Krypto-)Obfuscation" enthält die
Abschnitte
(Im Deutschen wären statt 'Decompiliern' und 'Obfuscation' auch die Schreibweisen ('Dekompilieren' und 'Obfuskation' möglich.)
zum Seitenanfang / zum Seitenende
Gute Software zu schreiben erfordert Können, Mühe, Sorgfalt und Kreativität. Wer von der Softwareentwicklung lebt, verkauft zwar seine/ihre fertigen Programme, möchte aber den Quelltext oft geheim halten. Nur dann kann er/sie auf Wartungsverträge bzw. Anschlussaufträge hoffen, beispielsweise wenn die Anwendung erweitert oder an neue Umstände angepasst werden muss. Der Programmtext ist geistiges Eigentum der Programmiererin bzw. des Programmierers und soll es auch bleiben. Deswegen wäre es schön, wenn technische Mittel verhindern, dass der Quelltext von jedem eingesehen, studiert, in Stücken weiter verwendet oder abgeändert werden kann. Kriminelle Verletzungen des Urheberrechts sollten am besten gar nicht erst möglich sein.
Leider bietet Java hier besonders wenig Schutz. Zwar bleiben die .java-Dateien mit dem Quelltext beim Software-Entwickler/der Software-Entwicklerin. Es wird nur das daraus erzeugte Programm als .jar-Datei weiter gegeben. In der jar-Datei befinden sich 'nur' die .class-Dateien mit dem compilierten Byte-Code für die virtuelle Java-Maschine. Daraus lässt sich aber mit geringem Aufwand der Quelltext mit allen Bezeichnern (also den sprechenden Variablen-, Methoden- und Klassennamen) ‚zurück' gewinnen (deshalb: reverse engineering) - nur die Kommentare fehlen. Dies und mögliche stärkere Schutzmaßnahmen sollen gleich gezeigt werden.
Dafür wird außer dem installierten Java-SE-Development-Kit ('Java-JDK', hier z.B. der 32-Bit-Version jdk-8u301-windows-i586.exe von https://www.oracle.com/java/technologies/javase/javase8u211-later-archive-downloads.html) nur folgende ebenfalls kostenlose Software verwendet:
Die Versionen und Quellen entsprechen dem Stand von Ende Januar 2022, auch wenn JD-GUI noch einen Copyright-Hinweis von 2012 enthält (und manche hier nicht benutzte Neuerungen der letzten Java-JDKs nicht kennt). Die letzten drei Programme sind angenehm kompakt.
zum Seitenanfang / zum Seitenende
Zunächst wird ein einfaches Javaprogramm geschrieben (Entwurfstechniken für komplexere Programme finden sich auf meinen Seiten zum Software-Engineering 1 und 2).
Als Beispiel soll ein Programm reichen, das die Zweierpotenz einer eingegeben Ganzzahl bestimmt, also z.B. nach Eingabe von 3 das Ergebnis 8 (=23) berechnet und anzeigt. In der Variante A erfolgt die Rechnung mit einer for- bzw. Zähl-Schleife:

Interessanter ist der selbstgeschriebene Inhalt in der vom Javaeditor leer angelegten Methode bOK_ActionPerformed, die beim Drücken des O.K.-Buttons aufgerufen wird:
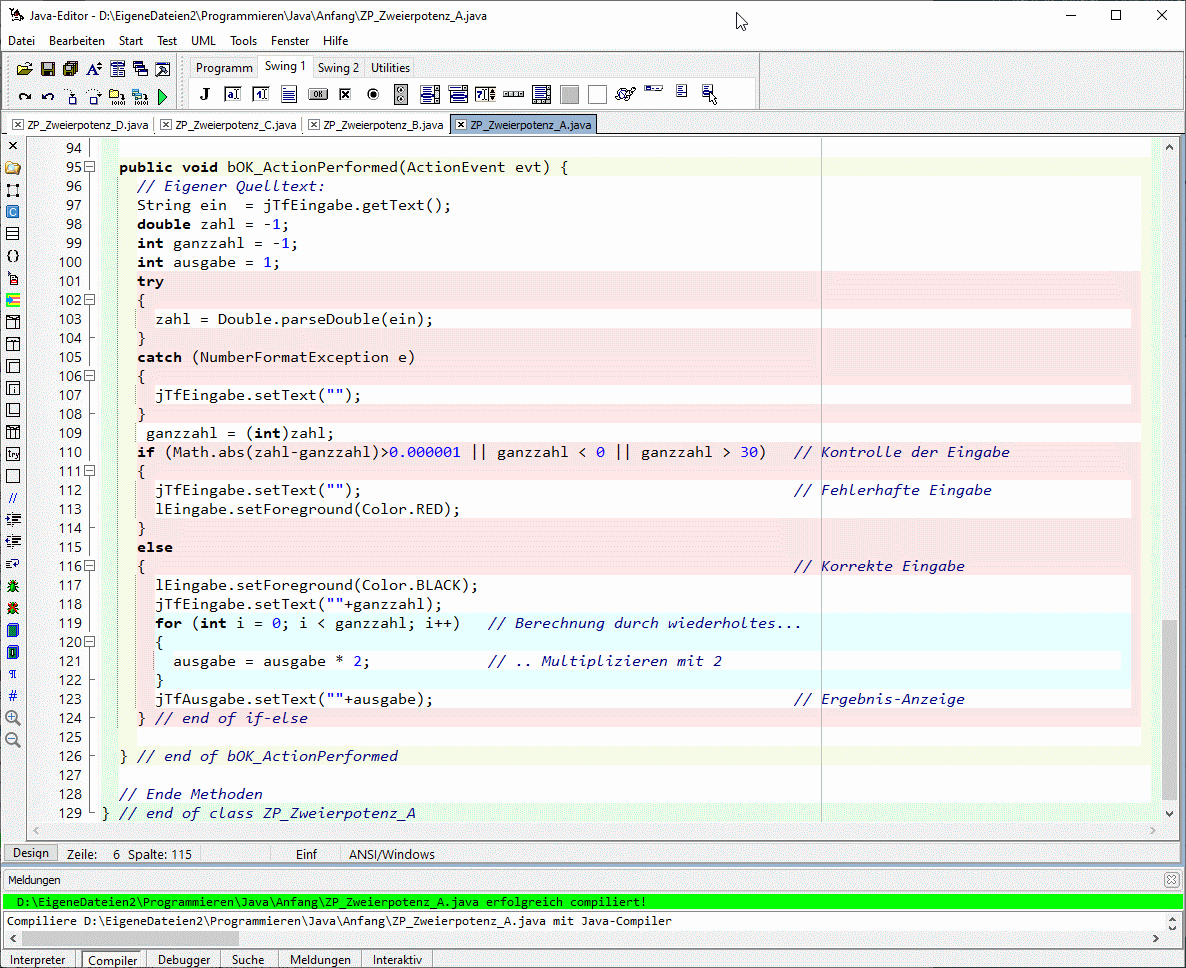
Die Zeilen 101 bis 114 dienen der Eingabe-Kontrolle. Wurde nichts oder etwas anderes als eine Kommazahl eingegeben, misslingt die Umwandlung in Zeile 103 und die fehlerhafte Eingabe wird gelöscht (Z. 107). Außerdem behält zahl den Wert -1 (aus Z. 98), sodass in Z. 109 auch ganzzahl den (unzulässigen) Wert -1 annimmt, was in Z. 110 bemerkt wird. Deshalb wird die Eingabe nochmal gelöscht (in Zeile 112; auf Zeile 107 hätte also verzichtet werden können). Außerdem wird die Schrift "Eingabe einer Ganzzahl zw. 0 und 30" rot angezeigt (Z. 113), um den Benutzer auf seinen Fehler hinzuweisen bzw. ihm eine erneute, jetzt korrekte Eingabe abzuverlangen.
Die Zeilen 112 und 113 werden im Übrigen auch dann ausgeführt, wenn zwar eine Zahleingabe erfolgte, aber die Zahl eine Kommazahl ist, die um mehr als ein Millionenstel von der nächsten Ganzzahl abweicht, oder zwar ganz, aber negativ oder größer als 30 ist.
Insofern wird der Block von Zeile 116 bis Zeile 124 wirklich nur ausgeführt, wenn eine korrekte Eingabe vorliegt bzw. tatsächlich eine ganzzahl zwischen 0 und 30 erkannt wurde.
Zunächst wird dann (in Zeile 117) die Schrift über dem Eingabe-Textfeld sicherheitshalber (wieder) schwarz gefärbt: Eventuell war sie von einer vorangehenden Fehleingabe noch rot; sonst stört das unnötige Schwärzen aber nicht und ist weniger aufwändig als eine zusätzliche Abfrage. Dann wird in Zeile 118 die ganzzahl im Eingabefeld angezeigt (und ersetzt evtl. eine Eingabe wie 3.999999999 oder 4.0 durch die stattdessen verwendete 4). Die eigentliche Berechnung der Zweierpotenz erfolgt anschließend in den Zeilen 119 bis 122. Weil die ausgabe zuvor (Z. 100) mit 1 initialisiert war, ist das auch das richtige Ergebnis für die Eingabe bzw. die ganzzahl = 0, wenn die Schleife gar nicht ausgeführt wird. Aber auch alle anderen erlaubten Werte von ganzzahl führen zum richtigen Ergebnis in ausgabe (während bei ganzzahl-Werten > 30 das Ergebnis den 32-Bit-Ganzzahl-Bereich von Java überschreiten und nicht mehr in ausgabe passen würde, wo dann ohne Fehlermeldung ein abgeschnittener und daher falscher Wert erschiene).
Zeile 123 schreibt das Ergebnis schließlich ins Ausgabe-Textfeld.
zum Seitenanfang / zum Seitenende
Das war jetzt nicht sehr schwer oder besonders kreativ, sondern diente nur dazu, ein Programm zu haben, zu compilieren und in eine .jar-Datei zu packen. Im Javaeditor geschieht letzteres über das Menü Start > Jar-Datei > Erzeugen. Es empfiehlt sich, vorher den Java-Quelltext alleine in einem eigenen Ordner abzuspeichern und dort zu compilieren, weil sonst auch fremde .class-Dateien aus dem gleichen Verzeichnis mit ins Archiv ZP_Zweierpotenz_A.jar gepackt werden. Diese .jar-Datei kann an eine beliebige Stelle kopiert oder weiter gegeben und dort ohne Quelltext oder Javaeditor bzw. Entwicklungsumgebung durch Doppelklick als eigenständige Anwendung gestartet werden (sofern im Zielsystem wenigstens eine Java-Runtime-Umgebung JRE installiert ist).
Wer das Programm ausprobieren (oder wie nachfolgend beschrieben weiter untersuchen) will, kann meine Datei "ZP_Zweierpotenz_A.jar" hier herunter laden (nach Klick 'Speichern', 'Datei speichern', 'Speichern unter..' o.ä. wählen!).
Wer ZP_Zweierpotenz_A.jar auf seinem Rechner hat, hat aber nicht nur die lauffähige Anwendung, sondern -- normalerweise zum Leidwesen des Programmierers, wenn nicht (wie hier) das reverse engineering ausdrücklich erlaubt sein soll -- hat damit auch viele nur schlecht verborgene Informationen über den Quelltext erhalten.
zum Seitenanfang / zum Seitenende
Startet man nämlich den Java-Decompiler JD-GUI (s.o.) und öffnet damit das herunter geladene Archiv ZP_Zweierpotenz_A.jar auf dem eigenen Computer, so kann man links im Baum navigieren, findet u.a. die Methode bOK_ActionPerformed(...) und kann sich durch einfachen Klick deren Quelltext anzeigen lassen:
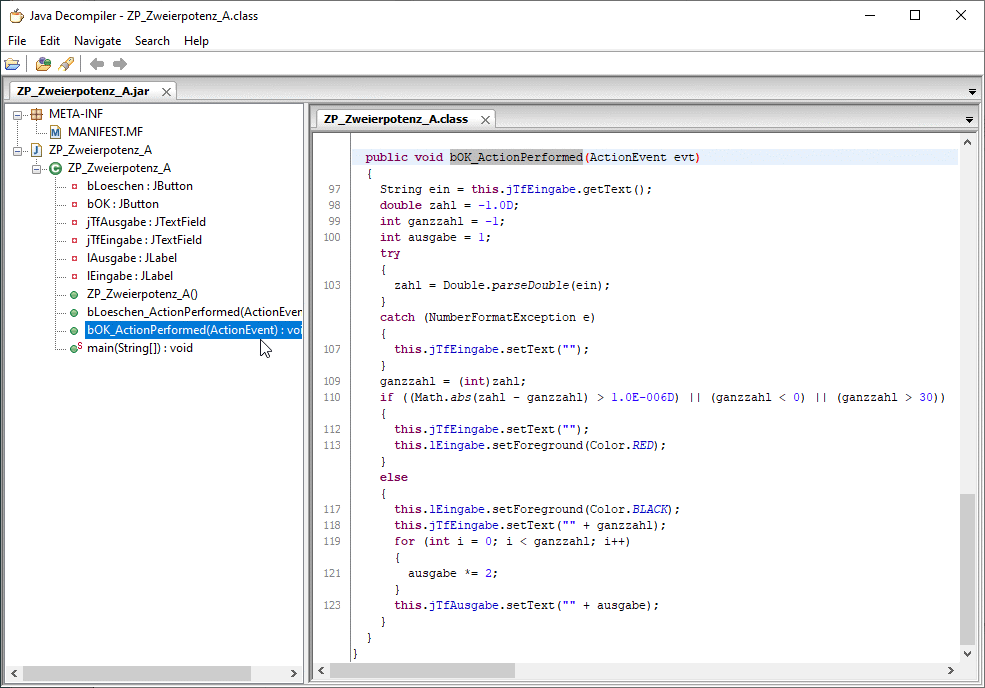
Der angezeigte Programmtext stimmt einschließlich der Zeilennummern und der Struktur mit meinem Original überein; nur die Kommentare fehlen. Anweisungen oder Konstanten können allerdings auch mal in synonymer Schreibweise erscheinen (z.B. 1.0E-006D statt 0.000001 in Zeile 110 oder ausgabe *= 2 statt ausgabe = ausgabe * 2 in Zeile 121), was aber ebensowenig stört, wie viele eingefügte "this.".
Der angezeigte Quelltext kann aus JD-GUI mit File > Save Source bzw. File > Save All Sources in eine (oder mehrere) .java-Datei(en) gespeichert und so später (wenn i.A. auch unerlaubterweise!) beliebig bearbeitet und weiter verwendet werden. Abweichende Original-Zeilennummern werden als Kommentare angezeigt. Das geistige Eigentum der Programmiererin/des Programmierers liegt völlig offen.
zum Seitenanfang / zum Seitenende
Wer das Auslesen des Quelltextes erschweren will, muss diesen verschleiern. Dies geschieht mit einem Obfuscator (to obfuscate = verschleiern, verwirren, vernebeln), hier z.B. mit ProGuard (s.o.). Nach dem Start wird in Input/Output mit Add input... die Datei ZP_Zweierpotenz_A.jargewählt. Außerdem muss mit Add Output... Pfad und Name der zu erzeugenden, verschleierten .jar-Datei angegeben werden (hier "ZP_A.jar" in einem anderen Ordner) (Die 'Library jars' im unteren Fenster wurden automatisch gefunden und brauch[t]en nicht verändert werden.)
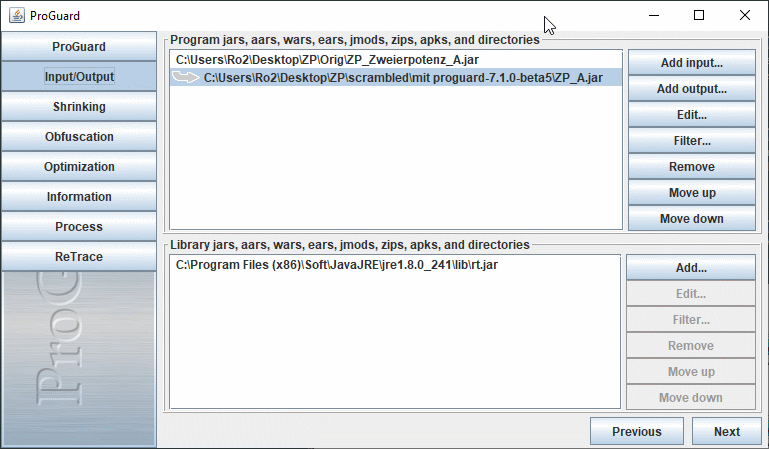
Die weiteren Schaltflächen auf der linken Seite (Shrinking, Obfuscation, Optimization..) öffnen Dialoge für zahlreiche Einstellungsmöglichkeiten, mit denen die Verarbeitung gesteuert bzw. das Ergebnis verändert werden kann. Ich habe es hier bei den Voreinstellungen von ProGuard belassen, sodass direkt mit Process und schließlich dort -- trotz eventueller Warnung, dass die Ausgabedatei leer bleibt, wenn sie nicht nach der Eingabedatei gewählt wurde -- mit Process! die Verwandlung erfolgreich in Gang gesetzt werden kann.
Leider zeigt ProGuard selbst nicht den Erfolg seiner Arbeit. Dazu muss die damit erzeugte Datei ZP_A.jar wieder mit einem Decompiler wie JD-GUI analysiert werden (vgl. Abschnitt c):
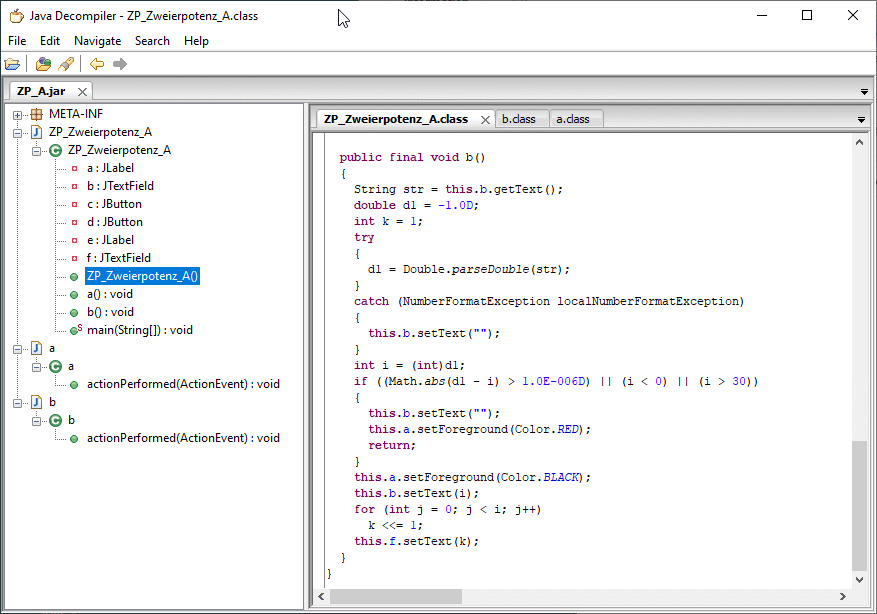
Man erkennt, dass die Zeilennummern fehlen, sprechende Namen durch einfache Buchstaben ersetzt wurden und auch die Anweisung im Schleifenkörper auf k <<= l; verändert wurde, was statt der Multiplikation der ausgabe (die jetzt offenbar k heißt) mit 2 einer Verschiebung ihrer Dualdarstellung um eine Stelle nach links entspricht (was natürlich zum gleichen Ergebnis führt).
In ProGuard war die Shrink-Option voreingestellt, womit die erzeugte .jar-Datei ZP_A.jar u.a. durch kurze Bezeichner möglichst klein gehalten wird. Mit anderen Optionen wären statt a, b, c... auch Bezeichner wie etwa OO100lO1ll0, Ol00lOll1l0,... möglich, die nur aus Kombinationen vom Großbuchstaben O, dem Kleinbuchstaben l und Nullen und Einsen bestehen, und für den menschlichen Betrachter schwer zu unterscheiden und auf den ersten Blick noch verwirrender sind. Allerdings können solche Bezeichner im gewonnenen Quelltext in jedem beliebigen Java- oder Text-Editor durch Suchen und Ersetzen leicht wieder in unterscheidbarere Namen verwandelt werden.
Außerdem besteht die Möglichkeit, durch zusätzliche Variablen und Kontrollstrukturen die erzeugte jar-Datei unnötig aufzublähen und damit dem menschlichen Leser die Analyse zu erschweren. Sinnlose Verzweigungen (if-Abfragen) können kompliziert aussehenden Programmtext enthalten, der wegen einer nicht-trivialen, aber nie erfüllbaren Bedingung aber gar nicht ausgeführt wird. Geschachtelte Wiederholstrukturen können weiteren nie benötigten Code enthalten oder den eingeschlossenen Programmblock genau einmal ausführen lassen.
Das Verteilen des Textes auf mehrere Dateien, Verstecken der Aufrufe von Math.abs oder setText in eigene Methoden (am besten in weiteren Klassen) mit nichtssagenden Namen, u.ä. wären zusätzliche Maßnahmen, um Zusammenhänge zu verschleiern. Der Fantasie sind kaum Grenzen gesetzt, und für Profi-Programmierer gibt es eine größere Auswahl sehr teurer kommerzieller Obfuscatoren, die ein reverse engineering angeblich nahezu unmöglich machen. Dass es aber umgekehrt auch Deobfuscatoren gibt, die die typischen Verwirrtechniken beliebter Obfuscatoren kennen und z.T. wieder aufheben können, sei nur am Rande erwähnt -- der Wettlauf von gegenseitigem Aufrüsten von Verschleierungs- und Entschleierungs-Verfahren überrascht nicht und entspricht dem Kampf zwischen Verschlüsslern und Codeknackern in der Kryptologie.
zum Seitenanfang / zum Seitenende
Da hätte man kaum gedacht, dass es doch 100%-ige Sicherheit geben soll. Laut dem Artikel
„Kryptografie - Der heilige Gral der Informatik"
in "Spektrum der Wissenschaft", Heft 12.21 (Dezember 2021), Seiten 70 bis 77, ist es Jain, Sahai und Lin in den USA 2020 nämlich gelungen, echte Sicherheit mathematisch zu beweisen:
siehe sdw_2021_12_S70.pdf (knapp 640 kB) von https://www.spektrum.de/pdf/070-077-sdw-202112-pdf/1944820.
Statt mit symmetrischen Verfahren zu ver- und entschlüsseln (bzw. zu ver- und entschleiern), sollen kryptografische Einwegfunktionen helfen (vgl. meine Seite Kryptologie II, auch wenn im Zeitschriften-Artikel nicht ‚mein' bzw. der RSA-übliche Divisionsrest einer Potenzfunktion, sondern elliptische Kurven als Beispiele für Einwegfunktionen vorgestellt werden).
Leider ist es bei der Krypto-Ofuscation nicht ganz so einfach wie bei Bankkarten: Dort ist die PIN (persönliche Identifikationsnummer, also die Geheimzahl) längst nicht mehr im Klartext, sondern nur als Hashwert auf der Kredit-, Debit- oder Giro-Karte gespeichert. Der Hashwert ist bei bekannter PIN leicht und schnell zu berechnen; umgekehrt kann aus dem Hashwert aber selbst mit größtem Aufwand die PIN nicht in überschaubarer Zeit ermittelt werden. Hashen gelingt also nur in eine Richtung, nicht umgekehrt, weswegen man von einer Einwegfunktion spricht. Außerdem ist die Einweg-Hashfunktion so gewählt, dass verschiedene PINs nur in extrem seltenen Fällen zum gleichen Hashwert führen können. Deshalb ist es gar nicht nötig, dass der Hashwert auf der Karte entschlüsselt wird (was, wie gesagt, ja auch praktisch unmöglich ist). Vielmehr kann der Bankautomat oder die Zahlstelle einfach aus der eingetippten PIN rasch deren Hashwert ermitteln und mit dem Hashwert auf der Karte vergleichen. Sind beide Hashwerte gleich, handelt es sich aller Wahrscheinlichkeit nach um gleiche PINs und somit um einen berechtigten Karten-Einsatz und die Zahlung wird freigeben. Übermittelt man hingegen nur den Hashwert eines Quelltextes, kann dieser sicher nicht als Programm ausgeführt werden. Ein Neueingeben des Programms zu Vergleichszwecken verbietet sich, da es nicht nur zu aufwändig wäre, sondern erst recht den Quelltext offen legen würde.
Verschlüsselt eine Autorin/ein Autor seine .jar-Datei hingegen mit seinem privaten Schlüssel z.B. per RSA-Verfahren, könnte der (aber auch jeder andere, unberechtigte) Empfänger die .jar-Datei mit dem zugehörigen öffentlichen Schlüssel des Programmierers oder der Programmiererin wieder in den Originalzustand zurück versetzen und ausführen. Der Empfänger wäre dann aber auch wieder in der Lage, einen Decompiler zu verwenden. Durch das Verfahren wäre höchstens die Urheberschaft beweisbar, nicht aber der Programmtext versteckt.
Es muss also eine Möglichkeit gefunden werden, eine .jar-Datei -- am besten unter Benutzung des öffentlichen Schlüssels des Empfängers -- so zu verschlüsseln, dass sie (nur) vom rechtmäßigen Nutzer nach Eingabe seines privaten Schlüssels zwar in ein lauffähiges Programm verwandelt wird, sich aber trotz gleicher Funktion von der ursprünglichen .jar-Datei deutlich unterscheidet und praktisch nichts vom ursprünglichen Quelltext preis gibt.
Im genannten Spektrum-Artikel wird die Suche nach solchen Möglichkeiten beschrieben. Leider ist das Ergebnis von 2020 offenbar noch wenig brauchbar. Man weiß wohl nur, dass es eine solche Möglichkeiten geben muss oder kann, hat aber offenbar noch kein praktikables Verfahren, eine solche Obfuskation wirklich zu erzeugen. Der Schlussabsatz des Artikels gesteht ein: „Allerdings sind die bisherigen Arbeiten rein theoretischer Natur: Selbst die einfachsten Programme würden durch eine solche Obfuskation zu gigantischen Ausmaßen aufgeblasen, was sie in der Praxis völlig unbrauchbar macht" (S. 77).
Dabei war der
Geheimhaltungsbegriff schon etwas abgeschwächt worden: Denn
die Funktion des Programms kann ja durch seine Reaktion auf
verschiedenste Eingaben getestet und ermittelt werden, ist also
nie geheim. Es sollte reichen, wenn aus der ausführbaren
Anwendung (hier also der .jar-Datei) nicht ermittelt werden kann,
auf welche Weise die Ausgabe erzeugt wird bzw. welcher
Algorithmus programmiert wurde (‚indistinguishable
Obfuscation [iO]'). Konkret: Würde für meine
Zweierpotenz irgendeine der vier gezeigten (oder auch jede
andere) Berechnungsmethode verwendet,
A: for (int i = 0; i < ganzzahl; i++) // Berechnung durch wiederholtes... { ausgabe = ausgabe * 2; // .. Multiplizieren mit 2 } B: for (int i = 0; i < ganzzahl; i++) // Berechnung durch wiederholtes... { ausgabe = ausgabe + ausgabe; // .. Addieren mit sich selbst // (um Verdoppelung zu erreichen) } C: ausgabe = (int)Math.pow(2,ganzzahl); // Nutzung der Potenzfunktion für // Kommazahlen aus der Java-Math-Bibliothek D: ausgabe = 1<<ganzzahl; // Bit-Operation: schiebt die Dualdarstellung // von 1 um ganzzahl Stellen nach links |
sollte es reichen, wenn man an/aus der verschleierten und der daraus letztlich erhaltenen ausführbaren Datei nicht mehr erkennen kann, welches der aufgeführten Verfahren ursprünglich programmiert wurde. Mit der Verwandlung von "ausgabe = ausgabe * 2" in "k <<= 1" (was "k = k << 1" bedeutet) wurde von ProGuard schon ein erster Schritt zur Verwischung der Unterschiede von A und D getan, aber sicher längst nicht genug. Außerdem steckt auch in der Programmierung der Oberfläche und der vielen restlichen Zeilen und Strukturen schützenswerte Arbeit.
Für eine detailliertere Übersicht über die skizzierten und weitere Krypto-Ansätze und zum aktuellen Forschungstand sollte der zu Beginn dieses Abschnitts e genannte und verlinkte Zeitschriftenartikel studiert werden. Dort wird auch von der Idee berichtet, Teile des Schlüssels und des Entschlüsselungsmechanismus' mit im Programmtext zu verstecken, sodass sich das per Obfuskation gesicherte Programm zwar bei der Ausführung nach und nach selbst entschlüsseln (und so lauffähig werden) kann, jeder Decompilier-Versuch aber nur das unlesbar verschlüsselte Programm mit dem ununterscheidbar eingemischten Schlüssel als Gesamt-Zeichenbrei, aber nichts Verständliches liefert.
zum Seitenanfang / zum Seitenende
Auch ohne
Decompiler lässt sich sehen, dass eine nicht mit einem
Obfuscator behandelte .jar-Datei die Originalbezeichner
enthält. Eine .jar-Datei ist nämlich eine ganz normale
.zip-Datei, die nur eine andere Dateiendung (".jar") erhalten
hat, um sie dadurch Java zuzuordnen. [Damit man die Endungen auch
sehen kann, setzt man in Windows im (Windows- bzw. Datei-)
Explorer im Menü bzw. Ribbon Ansicht das Häkchen vor
Dateinamenerweiterungen].
Benennt man nun (trotz Warnung, dass sie dadurch vielleicht
unbrauchbar wird) die Datei ZP_Zweierpotenz_A.jar aus dem Abschnitt
b in ZP_Zweierpotenz_A.zip um, kann man sie im Explorer (oder
mit einem [Un]Zip-Programm) entpacken (extrahieren) und den
Inhalt sehen. Außer der Manifestdatei (mit den Angaben zum
Start) wurden im Beispiel drei .class-Dateien erzeugt, die
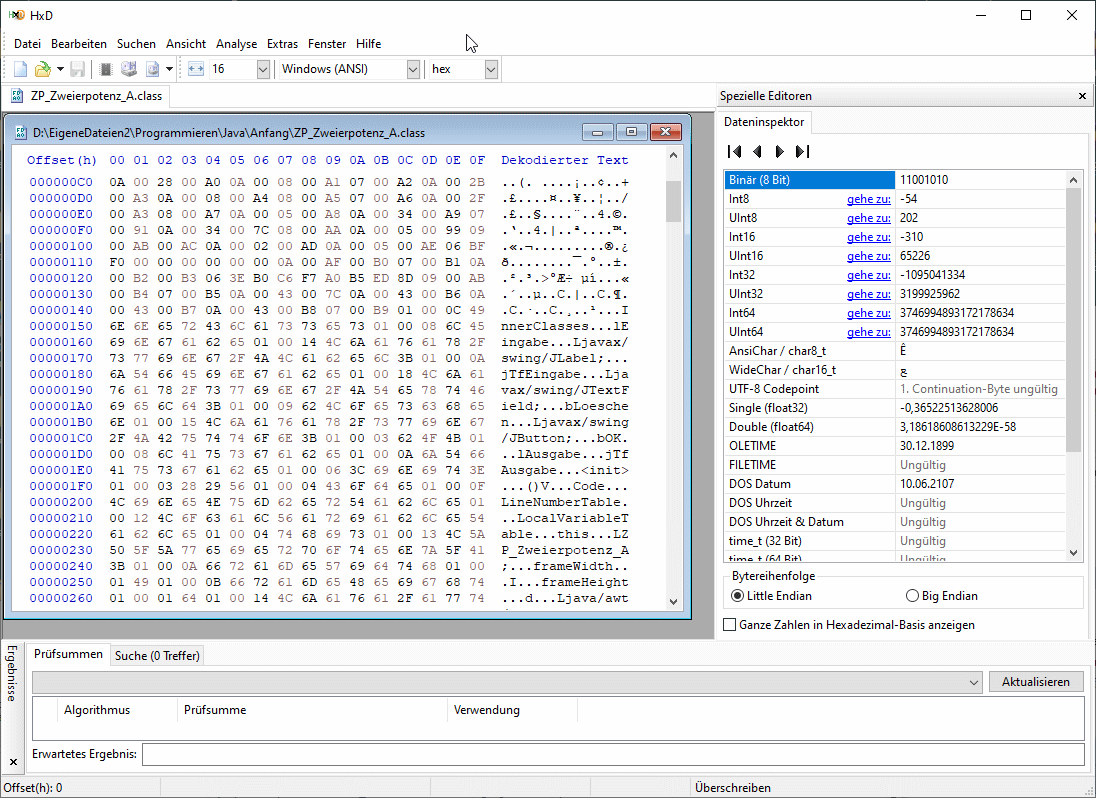
nacheinander mit einem HexEditor inspiziert werden können.
Neben unverständlichem Zeug sind die Bezeichner beim
Durchscrollen klar zu lesen -- was gezeigt werden sollte. Ein
Decompiler (wie oben JD-GUI) liefert aber mehr
und zeigt verständlich den kompletten Programmtext an, nur
eben ohne die ja für Menschen gedachten Kommentare, die
schon beim Compilieren übersprungen wurden und somit nie in
die .class-Datei(en) für die (Virtuelle) Maschine geraten
sind.
zurück zur Informatik-Hauptseite
(Die anderen Java-Seiten werden am besten auf der Informatik-Hauptseite ausgewählt)