Willkommen/Übersicht  >  Informatik  >   Informatik-Seite k)

Informatik mit Java

Teil k):  Kryptologie II

Eine vollständige Übersicht aller meiner Seiten "Informatik mit Java" gibt's auf der Informatik-Hauptseite!

In Teil j): Kryptologie I waren aufgeführt: Kryptologie -- Hauptzweige und Ziele, 1. Steganografie, 2. Symmetrische Chiffrier-Verfahren [2a) Skytale, 2b) Cäsar, 2c) monoalphabetische Substitution, 2d) Vigenère-Verfahren / polyalphabetische Substitution], 3. Verschlüsselung ohne Weitergabe eines Schlüssels (Shamir's no-key-Algorithmus).

Auf dieser Seite "Kryptologie II" finden sich folgende Kapitel und Abschnitte

• 4. Die Funktion f: f(x) = g^x mod p = g^x % p
• 4a) f(x) = g^x % p als Einwegfunktion
• 4b) Die Berechnung von g^x % p sowie das square-and-multiply-Verfahren
• 5. Schlüsselvereinbarung nach Diffie, Hellman und Merkle (mit interaktivem Applet)
• 6. Das RSA-Verfahren (mit interaktivem Applet)
• 6a) Beschreibung und Ablauf des RSA-Verfahrens sowie sein Korrektheitsbeweis
• 6b) Das Primzahlsieb des Eratosthenes
• 6c) Einfacher Euklid-Algorithmus zur Bestimmung des größten gemeinsamen Teilers ggT
• 6d) Zwei Verfahren zur d-Bestimmung: Probieren und der Erweiterte Euklid-Algorithmus
• 6e)  Sicherheit und Anwendung des RSA-Verfahrens
• 7. Digitale Signatur und Hash-Verfahren (sowie Krypto-Obfuscation)
• Passwortsicherheit, Nachwort und Ausblick (einschl. Sicherheitsrisiko durch Quantencomputer und nötiger Post-Quanten-Verschlüsselung)
• 
  

zum Seitenanfang / zum Seitenende

4. Die Funktion f: f(x) = g^x mod p = g^x % p

4a)  f(x) = g^x % p  als Einwegfunktion

Bei den folgenden kryptologischen Verfahren spielen Einwegfunktionen eine entscheidende Rolle. Einwegfunktionen sind Funktionen, bei denen man zu jedem gegebenem x aus dem Definitionsbereich (hier i.A. natürliche Zahlen) leicht und effektiv y = f(x) berechnen kann. Aber zu bekanntem y aus dem Wertebereich soll es so gut wie unmöglich sein, in angemessener Zeit das oder ein passendes x = f ^-1(y) zu bestimmen. (Die Schreibweise f ^-1 soll deutlich machen, dass die Funktion durchaus bijektiv sein dürfte. Falls nicht, soll es trotzdem ganz schwer sein, auch nur irgendein x mit f(x)=y zu finden).

Der gern gewählte Funktionstyp y = f(x) = g^x mod p = g^x % p nutzt das Potenzieren bzw. eine Exponentialfunktion mit Restbildung. Während die Potenzen mit natürlichen Exponenten leicht durch Multiplizieren bzw. -- wie wir im Abschnitt 4b) noch sehen werden -- durch duale Exponentation berechnet werden können, ist das Logarithmieren deutlich schwerer (Problem der Berechnung des diskreten Logarithmus): Hierfür gibt es kein einfaches Rechenverfahren. Letztlich müssen verschiedene Exponenten ausprobiert werden. Die zusätzliche Restbildung in der (Original-)Funktion sorgt dafür, dass die y-Werte alle im Bereich von 0 bis p-1 liegen und keineswegs mit steigendem x automatisch größer werden, sondern scheinbar regellos hin und her schwanken. Insofern hat man nach einer Probe keinen Anhaltspunkt, ob man lieber ein größeres oder kleineres x nehmen muss, um dem gewünschten Ergebnis y näher zu kommen. Man kann nicht gezielt auf das richtige x hin arbeiten, sondern es müssen letztlich alle x ausprobiert werden. Dazu nimmt man als Modulus p am besten eine Primzahl und als Basis g eine so genannte Primitivwurzel von p: dann nimmt für natürliche x aus dem Bereich von 1 bis p-1 das zugehörige y jeden Wert zwischen 1 und p-1 genau einmal an und man hat eine bijektive Abbildung, die den vollen Wertebereich von 1 bis p-1 nutzt. So hat man die Maximalzahl verschiedener y-Werte und erzwingt besonders langes Probieren, um ein richtiges x zu finden! (x=0 wird nicht zum Definitionsbereich zugelassen, weil damit immer y=1 wird und dafür die Umkehrung x=0 bekannt wäre).

Beispiel mit p=7 und g=3, also f(x) = 3^x % 7

Für x = 7, 8, 9, 10,.. wiederholen sich die Ergebnisse 3, 2, 6, 4, 5 und 1 immer wieder in gleicher Reihenfolge! g = 4 hingegen ist keine Primitivwurzel von p=7: Bei y=4^x % 7 treten als Ergebnisse nur die drei verschiedenen Reste 1, 2 und 4 auf, sodass eine Umkehrung bzw. das Finden eines passenden x wegen weniger nötiger Proben leichter wäre.

In Wirklichkeit werden natürlich nicht so kleine Zahlen genommen -- die wären schnell durchprobiert. Sondern man nimmt etwa Primzahlen p mit über 100 Dezimalstellen, sodass über 10¹⁰⁰ verschiedene y-Werte möglich und ebenso viele x-Werte nötig sind. Selbst ein schneller Rechner, der pro Sekunde eine Million Funktionswerte ermitteln könnte, bräuchte 10⁹⁴ Sekunden = 3,2 * 10⁸⁶ Jahre = 2,4 * 10⁷⁶ * (Alter unseres Universums), um so viele (x-)Werte zu durchzuspielen. Natürlich könnte schon relativ früh zufällig ein passendes x gefunden werden, aber im Mittel ist die Hälfte der angegebenen Zeit nötig -- was abschreckend genug wirken sollte. Selbst 20-stellige Primzahlen p mit Rechenzeiten um 10000 Jahren sind demnach ausreichend, sofern die Rechengeschwindigkeit nicht ganz dramatisch erhöht werden kann, das Problem nicht auf viele Tausende Computer verteilt wird oder grundsätzlich bessere Berechnungsverfahren gefunden werden!

zum Seitenanfang / zum Seitenende

4b)  Die herkömmliche Berechnung von g^x % p
sowie das square-and-multiply-Verfahren

Auf herkömmliche Weise ermittelt man -- wie oben in der Wertetabelle angegeben -- erst die Potenz und dann den Rest:

• Mit dem Taschenrechner berechnet man y = g^x mod p = g^x % p für kleine Zahlen, indem man zunächst die Potenz g^x bestimmt, diese durch p dividiert und sich den ganzzahligen Teil des Ergebnisses merkt, um schließlich g^x - gemerkt*p = y zu rechnen [Beim zweizeiligen Taschenrechner kann auch direkt g^x / p = eingetippt werden. Dann geht man mit den Navigationstasten zur Rechnung zurück, ersetzt das Divisionszeichen durch ein Minus, rollt wieder ans Ende der Formel und gibt *GanzzahligerAnteil ein, den man aus der Ergebniszeile abschreiben kann, bevor man erneut die =-Taste für das Ergebnis y drückt].
• Auch mit Tabellenkalkulationsprogrammen lässt sich etwa mit der Formel  = Rest (Potenz(g;x); p) nur für recht kleine Zahlen g und x ein Ergebnis erhalten (wobei g, x und p durch Konstanten [konkrete Zahlen] bzw. besser durch entsprechende Zellbezüge ersetzt werden müssen). Nach Angaben des Herstellers Softmaker arbeitet die Excel-Rest-Funktion übrigens fehlerhaft und man soll statt der gleichnamigen kompatiblen Funktion in der Tabellenkalkulation Planmaker besser die korrigierte RestP-Funktion einsetzen. Bei obigen Beispielen konnte ich keinen Unterschied feststellen; vermutlich tritt der Fehler nur bei der Bestimmung von Resten von negativen Quotienten auf, denn auch viele Programmiersprachen haben damit Probleme, sodass die Restbestimmung von negativen Zahlen möglichst vermieden werden sollte.
• Aber auch für positive ganze Zahlen scheitert die Java-Anweisung int y = Math.pow(g, x) % p; schnell an den großen Potenzen:

Schon die Berechnung etwa von 4³⁰ % 7 gelingt wegen der 18-stelligen Zwischenergebnisse auf keine der genannten Weisen richtig!

Deshalb muss ein schnelles und besseres Verfahren zur Berechnung von g^x bzw. von y = g^x % p gefunden werden, das übergroße (und damit wegen der begrenzten Stellenzahl zwangsläufig ungenaue) Zwischenergebnisse vermeidet.

Will man zunächst nur g^x -- also etwa g¹³ -- berechnen, so kann man sich die Dualdarstellung des Exponenten zunutze machen: 13 = 8 + 4 + 0 + 1 = (1101)₂. Damit lässt sich g¹³ = g^8+4+0+1 = g⁸ * g⁴ * 1 * g¹ = g⁸ * g⁴ * g¹ schreiben, wobei zu beachten ist, dass g² = (g¹)², g⁴ = (g²)² und g⁸ = (g⁴)² ist. Erinnert man sich jetzt noch, dass die Dualdarstellung von 13 durch die von hinten nach vorne gelesenen Reste in der Kette 13 : 2 = 6 Rest 1, 6 : 2 = 3 Rest 0, 3 : 2 = 1 Rest 1 und 1 : 2 = 0 Rest 1 gefunden werden kann, ist der normale square-&-multiply-Algorithmus (=Verfahren der dualen Exponentation) praktisch fertig und in nebenstehendem Struktogramm dargestellt: Weil beim Divisionsrest-Verfahren zur Bestimmung der Dualdarstellung des Exponenten x zuerst das niederwertigste Bit gefunden wird, wird beim Multiplizieren mit der kleinsten Potenz g¹ begonnen. Hat die Dualdarstellung eine 0 (keine 1), wird die entsprechende Potenz von g nicht mit in die Multiplikation aufgenommen. Und der ganzzahlige Anteil der Division x : 2 wird wieder in der Variablen x gespeichert, sodass im Programm die Variable x immer kleiner wird und das Verfahren bei x=0 endet.

Dieses Verfahren ist schnell (der Aufwand, d.h. die Zahl der Schleifendurchläufe, hängt nur von der Länge der Dualdarstellung des Exponenten x ab, also nur von log₂(x)). Selbst Exponenten x mit 100 Dezimalstellen würden nur zu leicht machbaren 330 Schleifendurchläufen führen. Allerdings wird das Ergebnis weiterhin immer größer und übersteigt bei großen Zahlen schnell Integer. MAX_VALUE = 2³¹ - 1 = 2,1 Milliarden bzw. den Bereich der vom Computer darstellbaren Ganzzahlen.

Da man bei y = g^x % p aber nur den Rest der Potenz bezüglich der Division durch p sucht, kann man wegen (a*b)%p = (a%p)*(b%p) % p schon alle Faktoren modulo p nehmen und damit schon alle Zwischenergebnisse angenehm klein halten. Natürlich wird bei einem p mit 100 Dezimalstellen trotzdem der Ganzzahlbereich gesprengt, aber für p bis etwa 46340 reicht damit die übliche Ganzzahlarithmetik. Im Unterricht werden die zur Veranschaulichung der Verfahren verwendeten Zahlen eher kleiner sein (aber eben doch vielleicht größer als die oben herkömmlich schon nicht mehr berechenbaren Beispiele mit Zahlen weit unter Hundert). Und für einen Modulus bzw. Divisor über 46340 (und mögliche Zwischenergebnisse über 46340² = 2,1 Milliarden) enthält die in der Java-JDK mitgelieferte KlasseBigInteger offenbar eine Implementation des square-&-multiply-Verfahrens mit Modulus in der Methode modPow, die mit BigInteger y = g.modPow(x,p); aufgerufen werden kann.

Nachstehend der Programmtext für die im Schulunterricht und fürs Prinzip ausreichende int-Variante:

Die hier vorgestellte und berechnete Funktion g^x mod p spielt beim Diffie-Hellman-Merkle-Verfahren ebenso wie beim RSA-Verfahren eine entscheidende Rolle, wie nachfolgend gezeigt wird. Es kann mit nicht zu großen Zahlen auch gut "von Hand" (d.h. mit einem einfachen Taschenrechner und auf Papier) ausgeführt werden, wie mein Bild if-k-sq&mul.gif (61 kB) beispeilhaft zeigt.

zum Seitenanfang / zum Seitenende

5. Schlüsselvereinbarung nach Diffie, Hellman und Merkle

Wie schon auf meiner ersten Kryptologie-Seite bemerkt, besteht das große Problem bei den symmetrischen Verschlüsselungs-Verfahren darin, dass Sender und Empfänger über den gleichen Schlüssel verfügen müssen -- wenn man von dem in Kapitel 3 dargestellten Mehrfachaustausch von Botschaften absieht. Nach früherer Ansicht geht das nur, indem ein Partner den Schlüssel wählt oder erstellt, und diesen dann auf einem sicheren Weg zum anderen Partner transportiert. Der Schlüssel darf keinesfalls in fremde Hände fallen. Diffie, Hellman und Merkle veröffentlichten 1976 jedoch ein Verfahren, wie zwei Parteien mit einigem Hin und Her über einen unsicheren Weg jeweils die gleiche, als Schlüssel verwendbare gemeinsame geheime Zahl s erzeugen können. Ein Angreifer, der die vollständige Kommunikation der beiden Partner abhört, erfährt hingegen die Zahl s nicht und kann sie auch nicht ermitteln.

Dass die beiden von P1 und P2 berechnet Zahlen s tatsächlich gleich sind, liegt an s₁ = beta^A % p = (g^B % p)^A % p = (g^B)^A % p = g^B*A % p = g^A*B % p = (g^A)^B % p = (g^A % p)^B % p = alpha ^B % p = s₂, wobei sich der Beweis nur auf die bekannte Kommutativität A*B = B*A sowie auf (a*b)%p = (a%p)*(b%p) stützt. Und weil man zum Berechnen von s mindestens eine der geheim gehaltenen, nie versendeten Zahlen A oder B braucht, kann ein Angreifer, der alle vier übermittelten Zahlen p, g, alpha und beta abgehört hat, trotzdem s nicht berechnen.

Ein kleines Programm, das im Wesentlichen die im vorigen Kapitel 4b) dargestellte Methode potMod aufruft, hilft beim Berechnen von Beispielen. Jeder Partner hat in Wirklichkeit natürlich nur eine abgespeckte Version des Programms, kennt die gegnerische Geheimzahl nicht und muss das übermittelte alpha oder beta von Hand eintragen.

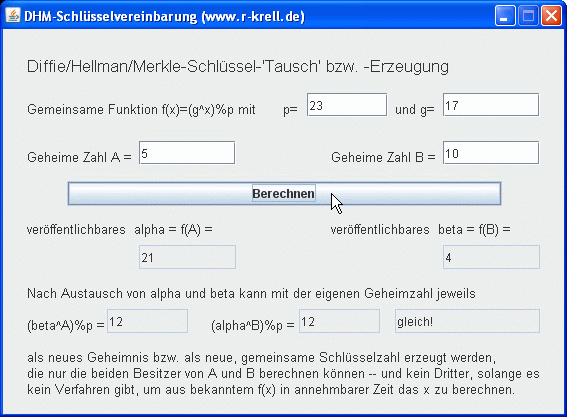
DHM-Applet auf Extraseite starten

Natürlich werden in Wirklichkeit weit größere Zahlen verwendet, als hier modellhaft dargestellt! Außerdem zeigt sich bei Beispiel-Rechnungen, dass die vielfach geforderte Einschränkung 1 < A < p-1 bzw. 1 < B < p-1 nicht unbedingt nötig ist, weil auch für größere A und B gleiche Schlüssel erzeugt werden. Natürlich würde anstelle eines großen A genauso das kleinere A' = A % p zum selben Ergebnis führen, sodass große Zahlen zumindest nicht nötig sind. A= p-1 (sowie A=0, A=p oder A=Vielfache von p) sollte(n) aber vermieden werden, weil dann immer alpha=1 und damit vorhersehbar s=1 wird. Und A=1 führt zu alpha = g, sodass ein Angreifer aus der Gleichheit von alpha und g auf A=1 und damit auf s=beta schließen kann. Analog sollte auf B=p-1 oder B=1 verzichtet werden.

Das Diffie-Hellman-Merkle-Verfahren taugt zur (aufwändigen) Erzeugung einer gemeinsamen Geheimzahl s, aber nicht zum direkten Verschlüsseln einer Nachricht. Man kann aber mit dem DHM-Verfahren einen gemeinsamen Schlüssel s erzeugen und dann mit einem anderen, symmetrischen Verfahren Nachrichten mit diesem Schlüssel s ver- und entschlüsseln. Die Sicherheit der Kommunikation hängt dann nur von der Sicherheit des verwendeten Chiffrierverfahrens ab, denn der Schlüssel s ist geheim: Wegen der Verwendung der Einwegfunktion f: f(x) = g^x mod p = g^x % p gibt es bei großen Zahlen g und p keine Möglichkeit, in sinnvollen Zeiten den Schlüssel s aus den eventuell abgefangenen ausgetauschten Werten g, p, alpha und beta zu ermitteln. Die häufig verwendete Bezeichnung des DHM-Verfahrens als "Schlüssel(aus)tausch" ist allerdings irreführend: es werden zwar Teilinformationen ausgetauscht, aber nicht der Schlüssel s selbst. Keiner der Partner weiß vorher, welche Zahl s erzeugt wird.

Im Internet findet man bei der Suche nach "Diffie Hellman" jede Menge Informationen. Deshalb hier nur eine kleine Auswahl:

• http://de.wikipedia.org/wiki/Diffie-Hellman-Schlüsselaustausch liefert den wie üblich guten Überblick, wenngleich dort auch die unsicheren A = 1 oder B = 1 zugelassen werden (mein A, B heißen dort a, b; mein alpha und beta entsprechen dort dem A und B).
• Wer's lieber als Film mag (in englischer Sprache): www.youtube.com/watch?v=40i9ujVJ040
• Leider im November 2012 abgeschaltet: http://betrieblicher-datenschutz-extern.de/artikel/verschluesselungstechnik-erklaerung-diffie-hellman-verfahren zeigte 2011 schön mit Beispielen, dass die Sicherheit des Verfahrens leidet, wenn man keine Primzahl p bzw. keine Primitivwurzel g wählt.

zum Seitenanfang / zum Seitenende

6. Das RSA-Verfahren

6a)  Beschreibung und Ablauf des Verfahrens sowie der Korrektheitsbeweis

Bevor weiter unten die einzelnen Komponenten des Verfahrens einzeln und mit Programmtexten ausführlich dargestellt werden, soll es hier zunächst als Ganzes beschrieben werden: Das RSA-Verfahren -- benannt nach seinen Erfindern Rivest, Shamir und Adleman, 1977 -- ermöglicht eine asymmetrische Verschlüsselung von natürlichen Zahlen (der Klartext muss zuvor also in eine oder mehrere Zahlen umgewandelt werden, die einzeln verschlüsselt werden. Um einen Angriff per Häufigkeitsanalyse zu verhindern, müssen die Buchstabengruppen [Blöcke], die zu einer Zahl führen, groß genug sein). Zum Verschlüsseln wird ein anderer Schlüssel (n, e) benutzt als zum Entschlüsseln (n, d). Aus der Kenntnis des Verschlüsselungs-Schlüssels kann der Entschlüsselungs-Schlüssel nicht hergeleitet werden. Deswegen kann jeder potenzielle Empfänger einer vertraulichen Botschaft vorab seinen Verschlüsselungs-Schlüssel veröffentlichen (public key). So wie in einem Telefonbuch die Telefonnummern vieler Teilnehmer eingetragen sind, damit man sie anrufen kann, können Personen oder Firmen ihre Verschlüsselungs-Schlüssel veröffentlichen, damit man ihnen damit verschlüsselte Nachrichten zusenden kann. Wer immer eine schützenswerte Mitteilung an eine Person oder Stelle schicken will, sucht deren öffentlichen Schlüssel aus dem Verzeichnis heraus (oder lässt ihn sich vom Empfänger mitteilen), chiffriert damit seine Nachricht und schickt sie an den Betreffenden. Selbst wenn die verschlüsselte Nachricht unterwegs abgefangen oder mitgehört wird, kann sie von keinem Angreifer entziffert werden (obwohl sich der Angreifer den öffentlichen Schlüssel des rechtmäßigen Empfängers ja leicht besorgen kann): Nur mit dem vom Empfänger geheim gehaltenen Entschlüsselungs-Schlüssel (private key) gelingt die Rückverwandlung in den Klartext. Dieser Entschlüsselungs-Schlüssel muss nicht transportiert werden und verbleibt ausschließlich im Besitz des Empfängers. Selbst der Absender, der Klartext, Geheimtext und den verwendeten öffentlichen Schlüssel kennt, ist nicht in der Lage, den geheimen Entschlüsselungs-Schlüssel des Empfängers zu berechnen. Egal, wie viele verschiedene Sender einem Empfänger schreiben: Jeder Empfänger braucht nur einen öffentlichen Schlüssel (den alle verschiedenen Sender verwenden können) und einen passenden geheimen Schlüssel, den er nicht aus der Hand zu geben braucht!

Anschaulich wird das RSA-Verfahren oft mit dem Posteinwurf in einen Briefkasten verglichen: Wer Postkarten (Mitteilungen) empfangen will, hängt für alle sichtbar einen Postkasten mit seinem Namen an die Haustür (= veröffentlicht den public key). Wer immer dem Briefkastenbesitzer eine Postkarte zukommen lassen will, kann zum Briefkasten gehen, die Briefkastenklappe über dem Einwurfschlitz anheben und die Nachricht einwerfen (= den öffentlichen Schlüssel benutzen): Ab Einwurf ist die Karte nicht mehr lesbar, weil sie vom Kasten geschützt wird (sozusagen verschlüsselt ist, wobei der Einwurfsschlitz ausreichend eng und der Briefkasten genügend tief und stabil sein soll, sodass Unbefugte nichts mehr herausholen können. Auch der Absender der Nachricht kommt nicht mehr an seine Karte, obwohl er sich den Briefkasten ansehen kann und weiß, was er eingeworfen hat). Ohne Falltür (=Briefkastentür) käme sogar niemand mehr an eine einmal eingeworfene Nachricht heran. Allerdings hat der rechtmäßige Besitzer einen private key, nämlich den Briefkastenschlüssel. Mit diesem lässt sich die ('Fall'-)Tür des Postkastens bequem aufschließen und lassen sich die Nachrichten zum Lesen entnehmen (Entschlüsselung mit Hilfe des geheimen/privaten Briefkasten-Schlüssels). Jeder Empfänger braucht nur einen Briefkasten, den alle Sender verwenden können. Der Besitzer muss seinen Briefkastenschlüssel, der zum aufgehängten Kasten passt, nie aus der Hand geben.

Das RSA-Verfahren nutzt natürlich wieder eine Einwegfunktion (entsprechend dem Einwerfen in den Briefkasten-Schlitz, wobei der Einwurf leicht ist, aber nicht leicht rückgängig gemacht werden kann), nämlich f(x) = x^d % n -- prinzipiell die bereits im 4. Kapitel vorgestellte Funktion, wobei jetzt aber die zu verschlüsselnde Zahl als Basis und nicht als Exponent eingesetzt wird. In diesem Fall spricht man von einer Einwegfunktion mit Falltür, weil mit zusätzlichen Kenntnissen über die Erzeugung von n die Bestimmung eines privaten Schlüssels möglich ist, der doch eine Umkehrung von f ermöglicht. Die Sicherheit des Verfahrens beruht darauf, dass man dem fertigen, veröffentlichten n nicht ansieht, aus welchen beiden Primzahlen p und q es durch Multiplikation entstanden ist: Während die Multiplikation p*q = n einfach ist, ist umgekehrt das Faktorisieren von n schwer und dauert selbst mit schnellsten Rechnern bei ausreichend großen Zahlen viele Jahrzehnte oder noch viel länger, darf jedenfalls nicht in vertretbarer Zeit gelingen. Die Faktoren p und q wären aber nötig, um daraus phi und damit (und mit e) das d des privaten Schlüssels berechnen zu können. Mehr zur Sicherheit und zur (richtigen) Anwendung des Verfahrens folgt noch im Abschnitt 6e)!

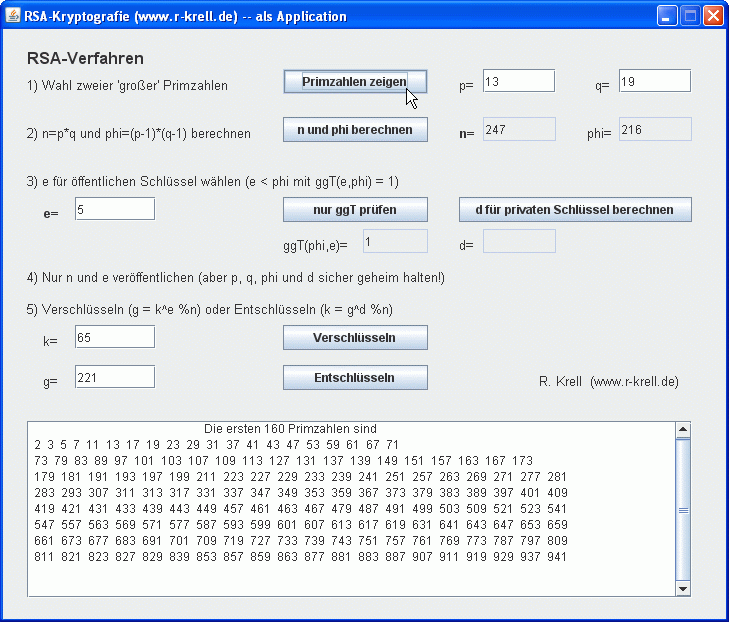
RSA-Applet auf Extraseite starten

Die Bildschirmansicht eines entsprechenden Java-Programms mit kleinen Modellzahlen zeigt beispielhaft das Prinzip des RSA-Verfahrens, das nachfolgend nochmal zusammengefasst werden soll:

Aus dem Schema ergeben sich verschiedene Aufgaben, die mit Computerhilfe gelöst werden:

• Bestimmung oder Überprüfung der Primzahl-Eigenschaft von p und q: Für Schulbeispiele, also noch einigermaßen kleine Primzahlen im Bereich bis einigen 100 000 (das ist sogar schon zu viel, wenn n und phi noch in int-Variablen passen sollen), reicht dazu das Sieb des Eratosthenes, das leicht mit einer entsprechend großen Reihung programmiert werden kann.
• Bestimmung bzw. Überprüfung der Teilerfremdheit von e und phi: Hierzu kann der größte gemeinsame Teiler etwa mit dem Euklid-Algorithmus berechnet werden. Ist der ggT zweier Zahlen gleich 1, so sind diese teilerfremd, d.h. sie haben keine gemeinsamen Teiler (>1).
• Bestimmung der Zahl d für den privaten Schlüssel: Hier ist bei kleinen Zahlen eine Art Probierverfahren mit verschiedenen Vielfachen von phi möglich; sonst liefert der erweiterte euklidische Algorithmus automatisch bei der ggT-Bestimmung von e und phi nebenher noch das passende d.
• Schließlich muss noch k^e % n bzw. g^d % n berechnet werden können: Das gelingt wieder mit dem in Kapitel 4 vorgestellten square-and-multiply-Algorithmus bzw. der dort gezeigten Methode potMod (die exemplarisch natürlich auch von Hand ausgeführt werden kann)!

Entsprechende Algorithmen bzw. Programmstücke werden von der gezeigten Oberfläche meines Programms "RSA-Kryptografie" aus aufgerufen und im Folgenden noch besprochen.

Der Beweis, dass die vom Empfänger entschlüsselte Zahl k_E = g^d % n tatsächlich der ursprünglichen Klarzahl k des Senders entspricht (also eine Entschlüsselung mit n und d überhaupt erfolgreich möglich ist, obwohl mit n und e verschlüsselt wurde), findet sich -- zusammen mit der Vorschrift für die Emittlung von d -- in der nachfolgenden, auch als pdf-Datei (28 kB) anseh- bzw. herunter ladbaren mathematischen Beschreibung, die das Lemma von Bézout und den Satz von Euler aus der Zahlentheorie nutzt:

Die Buchstaben für die zum Ver- und Entschlüsseln gebrauchten Zahlen e und d beziehen sich auf das englische encrypt (verschlüsseln) bzw. decrypt (entschlüsseln). Wegen der Kommutativität des Produkts e*d = d*e können sie ihre Rollen allerdings auch tauschen, wie wir noch im Kapitel 7 sehen werden.

Weiter unten, im Abschnitt 6d), werden zwei Verfahren zur Berechnung von d als Teil des privaten Schlüssels vorgestellt! Zunächst folgen aber Verfahren zur Primzahlberechnung (Abschnitt 6b)) und zur ggT-Bestimmung (6c)), während im Abschnitt 6e) Hinweise zur Sicherheit des RSA-Verfahrens folgen.

zum Seitenanfang / zum Seitenende

6b)  Das Primzahlsieb des Eratosthenes

Man notiert z.B. die ersten 99 999 natürlichen Zahlen, also 1, 2, 3, 4, 5, ..., 99 998, 99 999. Von diesen Zahlen wird zunächst die 1 gestrichen. Dann geht man zur nächsten ungestrichenen Zahl, erklärt diese zur Primzahl, lässt sie stehen, aber streicht alle ihre Vielfachen (Konkret: 2 bleibt stehen, aber 4, 6, 8, ..., 99 998 -- also hier alle geraden Zahlen als Vielfache von 2 -- werden gestrichen). Dann kehrt man zur letztgefundenen Primzahl zurück und geht von dort zur nächstgrößeren ungestrichenen Zahl, erklärt diese zur nächsten Primzahl, lässt sie stehen und streicht wieder ihre Vielfachen. Dies Vorgehen wird bis zum Erreichen des Endes der notierten Zahlen wiederholt.

Da Java-Reihungen mit dem Index 0 anfangen, müssen anfangs 0 und 1 gestrichen werden. Ansonsten gelingt die Umsetzung am besten mit einer boolean-Reihung, die zu jedem Index vermerkt, ob die (Index-)Zahl gestrichen wurde. Die am Ende ungestrichenen Zahlen sind die Primzahlen!

Für die in Wirklichkeit verwendeten Primzahlen von einigen Hundert Stellen Länge ist dieses Verfahren ungeeignet. Dann sind nur noch andere, z.T. stochastische Verfahren, machbar.

zum Seitenanfang / zum Seitenende

6c)  Einfacher Euklid-Algorithmus zur Bestimmung des größten gemeinsamen Teilers

Will man etwa den größten gemeinsamen Teiler von 385 und 84, also ggT(385, 84) bestimmen, so kann man 385 % 84 = 49;  84 % 49 = 35;  49 % 35 = 14;  35 % 14 = 7 und 14 % 7 = 0 berechnen. Endet die Kette bei Null, so war der Rest vorher bzw. ist der letzte Divisor das größte gemeinsame Vielfache: hier also ggT(385, 84) = 7. Im Interesse einer einfachen Programmierung setzt der folgende Algorithmus positive a und b mit a > b voraus:

zum Seitenanfang / zum Seitenende

6d)  Zwei Verfahren zur d-Bestimmung: Probieren und der Erweiterte Euklid-Algorithmus

In der mathematischen Begründung am Ende des Abschnitts 6a) wurde notiert, dass das natürliche d die Gleichung e*d = 1 + v*phi für ein ebenfalls positives, ganzes v erfüllen muss. Das ist gleichbedeutend damit, dass der Quotient  d = (1 + v*phi)/e  ganzzahlig ist, was wiederum äquivalent zu  (1 + v*phi )%e = 0  ist. Ein einfaches, für die kleinen Beispielzahlen in der Schule ausreichendes, aber für große Zahlen zu aufwändiges Verfahren berechnet einfach in einer Schleife für v = 1, 2, 3, ... nacheinander die Reste (1 + v*phi)%e für das gegebene phi und e. Erscheint der Rest 0, endet das Verfahren und das zugehörige v reicht zur Ermittlung von d = (1 + v*phi)/e. Zum gezielten Probieren braucht man allerdings das phi, von dem man ja verschiedene Vielfache v*phi einsetzt. phi gehört aber nicht zum öffentlichen Schlüssel und kann von einem Angreifer bei großem n wegen der Schwierigkeit, p und q zu finden, nicht in vernünftiger Zeit ermittelt werden. Insofern kann nur der Besitzer des privaten Schlüssels 'probieren'. Der folgende Programmtext enthält sowohl dieses Probierverfahren als auch den noch besser geeigneten Erweiterten Euklid-Algorithmus. Beide berechnen natürlich das gleiche d, sodass eine Methode reichen würde.

Wie in der mathematischen Begründung erwähnt, ist die genannte Darstellung e*d = 1 + v*phi  Folge der Teilerfremdheit von e und phi und der Vielfachsummendarstellung des ggT. Die Teilerfremdheit wird mit dem euklidischen Algorithmus aus 6c) durch ggT(phi,e) = 1 überprüft. Wird dieser Algorithmus um einige zusätzliche Variablen erweitert, kann während der Rechnung sukzessive eine Linearkombination s*e + t*phi =1 bestimmt werden ("Vielfachsumme"). Sind s und t bereits beide positiv, kann d=s gelten (v wäre dann gleich t, wird aber nicht weiter gebraucht). Ansonsten wird (u*e*phi - u*e*phi) = 0 auf der linken Seite von s*e + t*phi =1 ergänzt: 1 = s*e + u*e*phi - u*e*phi + t*phi = (s+u*phi)*e + (t-u*e)*phi = d*e + v*phi, d.h. d=s+u*phi und v=t-u*e wird nicht gebraucht.

Auch auf http://www.kilchb.de/krypt.htm wird eine rekursive Variante des EEA gezeigt (von Hand und in Delphi) und wegen ihrer Eleganz gelobt. Auf http://de.wikipedia.org/wiki/Erweiterter_euklidischer_Algorithmus werden zwar die rekursiven Varianten erläutert, aber z.Z. (Januar 2014) nur eine iterative Variante im Programmtext angegeben. Iterative Varianten finden sich auch z.B. auch im Matheprisma (das insgesamt eine empfehlenswerte Einführung in das RSA-Verfahren bietet), mit animiertem Übungsprogrammen bzw. Applets auf www.zum.de oder auf http://www.saar.de/~awa/infsek1/Berlekamp.htm und oft nicht nur bei der Suche nach Erweiterter Euklid-Algorithmus, sondern auch unter den Schlagwörtern Vielfachsummendarstellung oder Berlekamp-Algorithmus.

Beide Verfahren zur d-Bestimmung können natürlich auch von Hand ausgeführt werden (und sollten im Unterricht auch mehrfach geübt werden). Mein Bild if-k-eea-d.gif (59 kB) zeigt eine solche Beispielrechung, wobei sich für das Ausführen von Hand die rekursive Variante besser eignet. In meinem letzten Kurs wurde Ende 2013 der erweiterte Euklid-Algorithmus (EEA) übrigens sowohl im Mathematik- als auch im Informatikunterricht durchgenommen - in etwas unterschiedlichen rekursiven Darstellungen. Ein handgeschriebenes Blatt, das sich beim Anklicken als Bild in einem neuen Fenster bzw. einem neuen Reiter/einer neuen Registerkarte öffnet (oder mit Rechtsklick herunter geladen werden kann), zeigt ein Beispiel in beiden Versionen und macht deutlich, dass es sich nur um unterschiedliche Schreibweisen der gleichen Idee handelt:

Euklid-Algorithmus von Hand ausgeführt - 2 rekursive Versionen (if-k-eea-2.gif; 77 kB)

Als letzter Teil wird für die Berechnung von Geheim- oder Klarzahl beim RSA-Verfahren natürlich noch der square-&-multiply-Algorithmus wie in der bzw. aus der Methode potMod von Abschnitt 4b) bemüht (vgl. auch meine bereits dort genannte händische Beispielrechnung if-k-sq&mul.gif (61 kB) ).

zum Seitenanfang / zum Seitenende

6e)  Sicherheit und Anwendung des RSA-Verfahrens

Mit großen Zahlen -- Primzahlen von hundert oder mehr Dezimalstellen -- ist das RSA-Verfahren sehr sicher, weil in annehmbarer Zeit aus dem bekannten öffentlichen Schlüssel (n, e) trotzdem nicht der zum Entschlüsseln benötigte private Schlüssel (n, d) ermittelt werden kann (vgl. allerdings unten den Nachtrag zur Quantenbedrohung!). In der Literatur bzw. weiterführenden Webseiten werden allerdings auch Sonderfälle diskutiert, wie in Einzelfällen bei bestimmten Primzahl-Kombinationen die Stärke des RSA-Verfahrens etwas abnimmt (vgl. z.B. auch das Matheprisma-Beispiel). Werden die Schlüssel von einem bekannten TrustCenter bezogen, sollten sie ausreichend sicher sein. Auch könnte ein Angreifer, der dem Besitzer eines privaten Schlüssels gezielt einige (kleine) Klarzahlen unterschiebt und von diesem mit dem privaten Schlüssel verschlüsseln und das Ergebnis zurück schicken lässt, dadurch manchmal Hinweise auf den privaten Schlüssel erhalten. Hier sollte der Empfänger aufpassen, dass er nicht beliebigen fremden Text mit seinem privaten Schlüssel verschlüsselt -- vgl. Ausführungen im folgenden Kapitel 7. Und natürlich muss der private Schlüssel gegen physischen Diebstahl geschützt sein. Aber alles in allem ist das RSA-Verfahren, richtig angewandt, sehr sicher. (Wahrscheinlich ändert sich das aber schon in den Jahren 2030 bis 2035, wie unten im Nachwort beim Ausblick auf die Quantenbedrohung dargestellt!)

Viel wichtiger ist im Moment allerdings, dass bei falscher Verwendung des RSA-Verfahrens der Geheimtext auch ohne Kenntnis des privaten Schlüssels geknackt werden kann. Wird z.B. der Klartext buchstaben- bzw. zeichenweise in Zahlen verwandelt und diese werden dann einzeln mit dem RSA-Verfahren verschlüsselt, so liegt letztlich nur eine monoalphabetische Substitution vor. Wie schon auf meiner vorigen, ersten Kryptografie-Seite "Kryptologie I" im Abschnitt 2c) erwähnt, gelingt die Entschlüsselung sehr leicht mit einer Häufigkeitsanalyse. Die häufigste Geheimzahl steht wahrscheinlich für ein Klartext-'e', die zweithäufigste Geheimzahl steht vermutlich für ein 'n' im Klartext, dann folgen 'i' und 's', usw. Dabei muss man überhaupt nicht wissen, nach welchem Schema die Klarbuchstaben in die Klarzahlen verwandelt wurden und wie diese dann verschlüsselt wurden. Die Geheimzahlen müssen nicht in die Klarzahlen zurück gerechnet werden, sondern werden einfach als beliebige (unterscheidbare) Symbole für jeweils einen Klarbuchstaben aufgefasst.

Deshalb darf nie ein Buchstabe alleine, sondern muss immer ein großer Block von mehreren Zeichen gemeinsam verschlüsselt werden. D.h. die Codes mehrerer Buchstaben werden zu einer großen Klarzahl zusammengefasst (die dann für einen ganzen Block von Zeichen steht). Und natürlich muss n groß genug, nämlich noch größer als die größte Block- bzw. Klarzahl sein! Blöcke von etwa 50 Zeichen gelten heute als ausreichend sicher: Die Klarzahl ist dann z.B. die 150-stellige Zahl, die sich ergibt, wenn man einfach die (ggf. mit führenden Nullen jeweils auf drei Stellen aufgefüllten) ASCII-Codes der 50 Zeichen hintereinander schreibt. Längere Nachrichten werden in mehrere Textblöcke unterteilt. Für jeden Block wird die Klarzahl verschlüsselt, die zugehörigen Geheimzahl verschickt und vom Empfänger wieder entschlüsselt und in einen Textblock zurück verwandelt. Theoretisch wären 255⁵⁰ bzw. mindestens 26⁵⁰ = 5,6*10⁷⁰ verschiedene 50er-Blöcke möglich -- viel zu viele, als dass davon Blöcke mehrfach in normalem Text auftauchen würden und signifikante Wahrscheinlichkeiten hätten. Von zu kurzen Blöcken aus nur zwei oder drei Buchstaben ("Bi-" bzw. "Trigramme") gibt's hingegen nur wenige Hundert bzw. einige Tausend. Dafür ist eine Statistik möglich bzw. sogar für viele natürliche Sprachen bekannt (vgl. Verweise im Abschnitt 2c)) und solche Kurzblöcke könnten noch fast von Hand oder in kürzester Zeit mit dem Computer per Häufigkeitsanalyse und ganz ohne Entschlüsselungsnotwendigkeit identifiziert werden!

Leider ist trotz des schon recht effektiven potMod- bzw. square&multiply-Verfahrens die RSA-Ver- und (wegen meist d >> e vorallem die) -Entschlüsselung mit den nötigen vielstelligen Zahlen (z.B. ca. 200 Dezimalstellen für n und den 150-stelligen Blockzahlen k und bei meist nur knapp 10-stelligem e einem bis zu 190-stelligem d und 200-stelligen Geheimzahlen g) wohl sehr aufwändig und deutlich langsamer als symmetrische Verschlüsselungsverfahren. Deswegen werden heute in der Praxis meist hybride Verschlüsselungstechniken eingesetzt (z.B. bei "sicheren Internet-Verbindungen" auf/über https-Webseiten): Der eigentliche Nachrichtentext wird symmetrisch (etwa mit AES o.ä.) verschlüsselt, die extra dafür zufällig im Browser (wie dem Internet-Explorer, Opera, Firefox, Chrome usw.) erzeugte Schlüsselzahl wird noch im/vom Browser des Anwenders (Absenders) per RSA mit dem (mit der Webseite mitgeschickten) öffentlichen Schlüssel des Webseitenanbieters bzw. Empfängers (z.B. des Onlineshops oder der Bank) geschützt und zusammen mit dem chiffrierten Nachrichtentext ins Internet abgeschickt. Der rechtmäßige Empfänger kann dann zunächst mit dem RSA-Verfahren und seinem privaten Schlüssel die erhaltene Schlüsselzahl und dann damit und mit dem symmetrischen Verfahren die erhaltene Nachricht entschlüsseln. Unbefugte Dritte können hingegen den evtl. abgehörten Geheimtext nicht entschlüsseln, weil sie ohne den privaten RSA-Schlüssel nicht an den übermittelten AES-Schlüssel und ohne diesen nicht an den Klartext der Nachricht kommen.

Wie schon mehrfach erwähnt, werden in Wirklichkeit große Zahlen n und e verwendet. Ein Beispiel eines solchen tatsächlichen Schlüssels (dessen Ziffern platzsparend durch eine Kette druckbarer Ascii-Zeichen dargestellt sind und bei dem man dadurch leider auch nicht mehr sieht, wo n aufhört und e anfängt) findet sich auf meiner Seite "Kontakt, e-Mail", womit man mir entsprechend geschützte Mails senden konnte. Auch harmlose normale Briefpost versendet man üblicherweise im verschlossenen Umschlag - warum sollte man dann im Internet immer nur offen lesbare Nachrichten schicken?

zum Seitenanfang / zum Seitenende

7. Digitale Signatur und Hash-Verfahren

Im Vortext auf meiner ersten Kryptologie-Seite wurde auch der Authentizitätsnachweis als ein Ziel der Kryptologie genannt. In Zeiten von Phising-Mails ist es wichtig, dass sich Parteien im Internet ausweisen bzw. ihre Identität beweisen können. Das RSA-Verfahren (oder jedes andere asymmetrische Public-Key-Verfahren) bietet eine einfache Möglichkeit:

Hat der Partner, dessen Identität verifiziert werden soll, einen Schlüssel (n, e) veröffentlicht (und wird die Zugehörigkeit dieses Schlüssel zum Partner durch eine vertrauenswürdige Zertifizierungsagentur bzw. ein Trust Center bestätigt), so kann man ihm eine Zahl z, z < n schicken mit der Bitte, diese Zahl z mit seinem privaten Schlüssel (n, d) zu z' = z^d % n zu verschlüsseln und z' zurück zu senden. Jetzt kann man selbst den öffentlichen Schlüssel auf z' anwenden, d.h. z" = (z')^e % n berechnen. Gilt z"= z, so ist der Partner offensichtlich wirklich im Besitz des zu (n, d) komplementären privaten Schlüssels (n, e) und damit der, der als Inhaber des öffentlichen Schlüssels bekannt und zertifiziert ist. Ohne den privaten Schlüssel könnte ein Fremder kein z' erzeugen, das mit dem öffentlichen Schlüssel verschlüsselt wieder z ergibt!
Der überprüfte Partner muss allerdings ggf. aufpassen, dass nicht durch (viele) geschickt gewählte z Hinweise auf sein d erhalten werden können, er also praktisch durch einen chosen-plaintext-Angriff ausgespäht wird. Insbesondere könnte ein sehr kleines z = 2, 3, 4..., sodass auch z^d < n bleibt, wegen dann z' = z^d rasch zu d = log _z (z') = ln (z') / ln (z) führen.

Der geschilderte reine Identitätsnachweis reicht jedoch oft nicht: Was nützt die Kenntnis, dass der Inhaber einer bestimmten Mailadresse wirklich die Person oder Firma X ist bzw. war (weil er auf Nachfrage schon mal das richtige z' zurücksenden konnte), wenn ein Angreifer das Mailkonto gehackt haben und ebenfalls unter dem Namen X Mails verschicken könnte? Wichtiger ist, nachweisen zu können, dass ein bestimmtes übermitteltes Dokument tatsächlich von X stammt. Grundsätzlich ginge das dadurch, dass der Sender sein Dokument vollständig mit seinem geheimen, privaten Schlüssel per RSA-Verfahren verschlüsselt und die so berechnete Geheimzahl verschickt. Jeder Empfänger (egal ob der richtige Adressat oder ein Unberechtigter) kann dann die Geheimzahl mit dem öffentlichen Schlüssel des Absenders entschlüsseln und erhält die Klarzahl als numerische Repräsentation des verschickten Dokuments. Kommt ein sinnvoller, lesbarer Text heraus, dann wurde offenbar richtig verschlüsselt und der Sender ist verifiziert; seine Identität ist sicher und er kann auch später die Urheberschaft am Dokument nicht abstreiten (Tatsächlich könnte natürlich auch ein geheimer Schlüssel gestohlen werden -- Zertifizierungsagenturen geben daher die Schlüssel i.A. nur mit einer Gültigkeitsdauer von einem oder wenigen Jahren aus und führen außerdem Listen widerrufener Schlüssel. Wurde mit dem privaten Schlüssel zu einem gültigen, nicht widerrufenen öffentlichen Schlüssel verschlüsselt, gilt dessen Besitzer als Autor und Versender). Bei diesem Verfahren steht also nicht die Vertraulichkeit (Schutz vor unberechtigtem Lesen) des Dokuments, sondern der Änderungsschutz (niemand kann das Dokument unbemerkt inhaltlich ändern, wenn er nicht der Besitzer des privaten Schlüssels ist) und Identitäts-Fälschungsschutz (niemand kann sich für jemand anders ausgeben) sowie die Unbestreitbarkeit im Vordergrund. Die Vertraulichkeit wird gar nicht gewährleistet.

Wie allerdings schon beim Hinweis auf die hybriden Verfahren angemerkt, ist die RSA-Verschlüsselung umfangreicher Dokumente (insbesondere mit dem großen d des privaten Schlüssels) sehr aufwändig. In der Praxis garantiert man die Integrität/Unverändertheit eines Dokuments oder auch einer Binärdatei üblicherweise durch einen schnell erzeug- und überprüfbaren Hashwert. Ein Hashverfahren berechnet aus der digitalen Repräsentation eines Textes (also aus den Bits, aus denen die Datei besteht) eine Dualzahl, eben den Hashwert, der auch digitaler Fingerabdruck genannt wird und meist eine feste Stellenzahl hat.
Während einfache Prüfziffer-Programme etwa für die alte ISBN-Buchnummer oder die EAN-Artikelnummern i.W. gegen typische unabsichtliche Tipp- oder Lesefehler -- das Weglassen einer Ziffer, die Vertauschung zweier Nachbarziffern oder eine falsche Ziffer an Stelle einer richtigen -- schützen sollen, sind ihre Formeln leicht zu verstehen. Ist eine Prüfziffer und ein großer Teil des ursprünglichen Nummer bekannt, kann man die restlichen Ziffern leicht so bestimmen, dass die gleiche Prüfziffer herauskommt bzw. kann die Nummer so fälschen, dass trotzdem die gleiche Prüfziffer herauskommt und die gefälschte Nummer scheinbar gültig ist. Steht wie bei den ISBN-Nummern nur eine einzige Prüfziffer mit nur 11 verschiedenen Werten zwischen 0 und X zur Verfügung, werden jeweils viele verschiedene Buchnummern durch den Prüfalgorithmus auf die gleiche Prüfziffer abgebildet und eine bestimmte Prüfziffer kann nicht die Identität einer Nummer garantieren.

Gute Hashverfahren wollen mehr: Die Berechnung des Hashwerts soll mit einer Einwegfunktion erfolgen, sodass ein Rückrechnen, mit welchem anderen bzw. mit welchem veränderten Text die gleiche Prüfsumme erreicht werden könnte, praktisch unmöglich ist. Dazu muss sich die Prüfsumme schon bei geringfügigster Änderung des Textes unvorhersehbar bzw. dramatisch ändern, sodass nicht durch gezielte leichte Variationen an zwei verschiedenen Stellen des Textes wieder die gleiche Prüfsumme erreicht werden kann. Auch soll aus dem Hashwert nicht die Größe/Länge des gehashten Textes hervorgehen. Außerdem sollen die Hashfunktionen möglichst kollisionsfrei sein: am besten sollte es überhaupt keine zwei verschiedenen Texte geben, die zur gleichen Prüfsumme führen. Dies scheint angesichts der begrenzten festen Stellenzahl für die Prüfsumme unmöglich, weil sich ja prinzipiell unendlich viele verschiedene Texte erzeugen lassen. Nimmt man aber an, dass von z.Z. 6,5 Milliarden Erdbewohnern jeder einzelne während seines 50-jährigen Erwachsenenlebens täglich 100 Texte produziert, kämen auf diese Weise 'nur' 1,2*10¹⁶ verschiedene Texte zusammen (tatsächlich sind die Mehrzahl der Erdbewohner weit jünger und übertreffen mit der angenommenen Gesamtlebenszeit deutlich die Gesamtlebenszeit aller bisherigen Erdbewohner von Anbeginn der Menschheit an, sodass die wirkliche Zahl der bisher produzierten Texte viel geringer ausfallen dürfte). Eine Prüfsumme mit immer 128 Dualstellen (wie bei dem message digest md5) bzw. sogar 160 Dualstellen (wie beim secure hash algorithm sha1) kann aber 2¹²⁷ = 1,7*10³⁸ bzw. sogar 2¹⁵⁹ = 7,3*10⁴⁷ verschiedene Werte annehmen, übertrifft also die Zahl produzierter bzw. produzierbarer Texte bei weitem und um viele Größenordnungen. Insofern sollte praktische Kollisionsfreiheit möglich sein und damit praktisch eine ein-eindeutige Zuordnung zwischen Text und Prüfsumme, wenngleich wegen der Einwegfunktion aus der Prüfsumme nicht der zugehörige Text gewonnen werden kann (und darf) (während umgekehrt der Hashwert schnell und leicht aus dem Text berechnet werden können soll).

Damit ist jetzt folgender Weg für eine schnell auszuführende digitale Signatur möglich, die die Unverändertheit und die Urheberschaft eines Textes garantiert:

• Der Absender erstellt einen Text und berechnet den Hashwert seines Textes (etwa mit md5 oder sha1)
• Der Absender verschlüsselt den Hashwert, der im Vergleich zu typischem Text nur eine kleine Zahl ist, in annehmbarer Zeit mit seinem geheimen Schlüssel nach dem RSA-Verfahren
• Der Absender verschickt seinen (Klar-)Text und den verschlüsselten Hashwert gemeinsam an den Empfänger
• Der Empfänger trennt Text und verschlüsselten Hashwert und berechnet vom empfangenen Text mit dem gleichen Hash-Verfahren wieder die Prüfsumme
• Außerdem entschlüsselt der Empfänger mit dem öffentlichen Schlüssel des Absenders die erhaltene Geheimzahl des Hashwerts
• Stimmen entschlüsselter Hashwert und eigene Prüfsumme überein, kann als sicher gelten, dass der Text unverändert ist und vom richtigen Absender stammt. Sind hingegen entschlüsselter Hashwert und die eigene Prüfsumme unterschiedlich, wurde entweder der Text nachträglich verändert oder die Prüfsumme nicht mit dem richtigen geheimen Schlüssel verschlüsselt, stammt also aus einer fremden Quelle. Bei Ungleichheit muss also in jedem Fall ein Betrugsversuch befürchtet werden.

Die digitale Signatur ist weit sicherer als eine eigenhändige Unterschrift auf einem Blatt Papier: Auf dem Blatt könnten nachträglich noch Textänderungen angebracht werden und die Unterschrift könnte eingescannt werden, um z.B. auf einem Fax mit ganz anderem Inhalt missbräuchlich eingesetzt zu werden. Da die elektronische Signatur Attribute des Absenders (seinen privaten Schlüssel) und des Textes (dessen Hashwert) verbindet, ist sie an den Text und Absender gemeinsam gebunden und kann nicht in betrügerischer Absicht übertragen werden.

Weil die Prüfsumme (der Hashwert) mit 128 bzw. 160 Bits groß genug ist (tatsächlich werden i.A. jeweils vier Bits zu einer Hex-Ziffer zusammengefasst und die Prüfsummen als 32- bzw. 40-stellige Hexadezimalzahlen angegeben; die in Entwicklung befindlichen Verfahren  md6  und  sha2  arbeiten mit noch größeren Zahlen), kann aus der Kenntnis der Prüfsumme, der Geheimzahl der Prüfsumme und des öffentlichen Schlüssels auch nicht auf den privaten Schlüssel des Absenders geschlossen werden. Wegen der praktischen Unmöglichkeit, Texte zu produzieren, die bestimmte vorhersehbare Prüfsummen haben, kann auch mit vielen dem Absender zum Versand untergeschobenen Texten kein chosen-plaintext-Angriff auf seinen geheimen Schlüssel erfolgen!

Einer weitere interessante Anwendung der Kryptologie ist übrigens die Krypto-Obfuscation von Programmtexten, um Programmierideen gegen Ausspähen zu sichern - vgl. meine Seite l): Schutz der Programmierideen durch (Krypto-)Obfuscation mit einem interessanten, erst im Dezember 2021 bekantgewordenen Forschungsergebnis.

zum Seitenanfang / zum Seitenende

Nachwort, Passwortsicherheit und Ausblick

Die Kryptologie ist ein komplexes Gebiet, das in dem kurzen Abriss auf meinen beiden Webseiten keinesfalls erschöpfend behandelt werden konnte. Es gibt eine Reihe guter Bücher zur Kryptologie. Und im Internet finden sich zu allen angesprochenen Punkten viele zusätzliche Informationen, die -- wie viele weitere Verfahren oder Aspekte -- hier nicht berücksichtigt wurden, aber für ein vertieftes Verständnis lohnend oder sogar notwendig sind.

Für praktische Übungen und wegen der vielen in der mitgelieferten Hilfe, im Handbuch und verstreut enthaltener guter Erklärungs-Texte möchte ich außerdem ausdrücklich auf das kostenlose Werkzeug (J)CrypTool hinweisen, das ursprünglich entwickelt wurde, um Bankern die Notwendigkeit sicherer Verfahren für den alltäglichen Geldtransfer nahe zu bringen -- das aber auch für das Selbststudium oder den Unterricht gut geeignet ist. Und auch auf der zugehörigen Seite Crypttool-Online.org gibt's vieles zur Kryptologie, ohne dass das Tool herunter geladen werden muss.

Und natürlich erreicht man auch ein besseres Verständnis der Materie, wenn man neben den hier angegebenen eigene weitere (Hilfs-)Programme im Umfeld der Kryptologie schreibt -- angefangen mit der einfachen Analyse von Buchstabenhäufigkeiten bis hin zum Programmieren weiterer Ver- oder Entschlüsselungs-Verfahren oder der Erweiterung meiner Programme mit den Datentypen long oder BigInteger...

Heute sind kryptografische Verfahren überall in unserem Alltag anzutreffen. Jede https://-Webseite überträgt die Daten verschlüsselt; fast alle Messenger-Dienste nutzen mittlerweile Krytografie. Und anders als in den Anfängen vor 50 Jahren sind längst auf Bankkarten und in fast allen Passwortdateien nicht mehr die Passwörter selbst, sondern nur noch deren (md5-) Hashwerte abgelegt. Ergibt das vom Benutzer eingetippte Passwort die gleiche Prüfsumme, so wird von der Gleichheit bzw. der Zugangsberechtigung ausgegangen. Weil die Passwörter meist nur aus wenigen Zeichen bestehen, heute aber Programme im Umlauf sind, die -- z.T. unter Ausnutzung der Fähigkeiten moderner Grafikkarten -- auf einem normalen PC pro Sekunde über eine Million Passwörter erzeugen und ihre Prüfsumme bestimmen können, können Passwörter mit weniger als 6 oder 8 Stellen und insbesondere solche, die nur einen begrenzten Zeichenvorrat benutzen (also nicht Groß- und Kleinbuchstaben und Sonderzeichen und Ziffern, sondern etwa nur eine Zeichensorte) durch brute-force-Angriffe, also Durchspielen aller möglichen Zeichenkombinationen in wenigen Minuten bis einigen Stunden Rechenzeit ermittelt werden. 5-stellige PINs, die vor 30 Jahren vielleicht noch einige Tage Rechenzeit erfordert hätten, sind heute in Sekunden geknackt und überhaupt nicht mehr zeitgemäß, wenn ein Durchprobieren möglich ist. Im September 2024 werden mindestens 10 Zeichen empfohlen!

Möglicherweise steht durch schnellere oder massiv-parallele oder grundsätzlich andere Rechner (wie z.B. Quantencomputer, s.u.), vielleicht aber auch durch bisher noch unentdeckte Algorithmen für 'normale' Digital-Computer, die Unberechenbarkeit heutiger Einwegfunktionen in naher Zukunft auf dem Spiel. Allein wegen immer höherer Rechengeschwindigkeiten wurden in den letzten Jahren schon immer mehr Stellen nicht nur für Passwörter, sondern z.B. auch für die Primzahlen p und q des RSA-Verfahrens gefordert und eingesetzt...

Quantenbedrohung der bisherigen Verfahren
und Post-Quanten-Kryptografie (PQK)

Als Hauptbedrohung des oben dargestellten RSA-Verfahrens (und des ähnlichen Verfahrens mit Elliptischen Kurven, d.h. aller heute überall im großen Stil verwendeter Verfahren) gelten inzwischen die Fortschritte beim Bau immer leistungsfähigerer Quantencomputer. Sie arbeiten ganz anders als herkömmliche Digitalcomputer und nutzen quantenmechanische Effekte aus, die erlauben, dass Teilchen (die in QuBits zusammengefasst werden) gleichzeitig eine Vielzahl verschiedener überlagerter Zustände annehmen können. Mit dem schon 1994 theoretisch vorgestellten Shor-Algorithmus (vgl. z.B. Wikipedia) können hinreichend große Quantencomputer -- hier scheinen über 10.000 QuBits nötig, während die bisher besten Versuchscomputer allerdings erst über wenige Hundert QuBits verfügen und trotzdem kaum stabil gehalten werden können (Stand 2024), weswegen vielleicht noch ein Paar Jahre Zeit sind -- die bisherigen Einwegfunktionen wohl bald rückwärts berechnen. Dann können z.B. auch große Zahlen rasch in ihre Primfaktoren zerlegt werden und so aus dem öffentlichen Public Key der geheime Private Key errechnet werden, der zur Entschlüsselung gebraucht wird. Damit wären dann alle heute üblichen Verschlüsselungen zu knacken. Geheimdienste und manche Firmen sammeln schon jetzt abgefangene, z.Z. noch unlesbare Nachrichten, Baupläne und geheime Daten von Regierungen, Militärs oder von Konkurrenzunternehmen (zusammen mit den öffentlichen Schlüsseln, mit denen sie gesichert wurden). Ab der Verfügbarkeit ausreichend großer Quantencomputer (ab dem 'Q-Day') können sie dann die geheimen (privaten) Schlüssel errechnen und so die jetzt auf Vorrat gepeicherten Informationen lesen. Selbst Einzelpersonen sind gefährdet: Auch wenn die Online-Einkäufe, Kontobewegungen oder Chats der meisten Normalbürger in einigen Jahren vermutlich uninteressant sind, könnten künftige Politiker(innen) oder Prominente mit jetzt gesammeltem Material aus dem ganz normalen, heutigen privaten Onlineverhalten erpressbar werden oder ihr Ruf könnte durch die Veröffentlichung beschädigt werden.

Zwar weiß man inzwischen, dass neu zu entwickelnde, auf quantenmechanischer Verschränkung beruhende Verfahren (so genannte Quanten-Verschlüsselung) möglich und beweisbar sicher sein können und auch einem Angriff mit Quantencomputern standhalten würden. Es wäre an der übertragenen Information sogar erkennbar, ob ein Abhörversuch stattgefunden hat. Aber dabei handelt sich um Verfahren, die bisher nur in Physiklaboren mit speziellen Geräten und unter extrem hohem technischen Aufwand realisiert werden konnten. Trotzdem konnten dort bisher nur minimalen Datenmengen testweise übertragen werden. Quantenkryptografie wird daher in den nächsten Jahrzehnten sicher nicht allgemein verfügbar.

Deshalb sind so genannte Post-Quanten-Verschlüsselungen gesucht, die heute schon bzw. ab sofort auf ganz normalen Computern überall eingesetzt werden können, und trotzdem auch mit künftigen Quantencomputern nicht angreifbar werden. Zwar ist das klassische One-Time-Pad-Verfahren {OTP, siehe meine Seite j) Kryptologie I } immer -- auch gegen Angriffe mit Quantencomputern oder beliebiger, irgendwann noch zu erfindender Angriffarten -- vollkommen sicher, aber leider unpraktisch, weil ständig neue sehr lange Schlüssel gebraucht werden und ausgetauscht werden müssten. Seit einigen Jahren wird daher nach asymmetrischen Verfahren gesucht, die schnelle Verschlüsselung und (mit dem richtigen Schlüssel) auch einfache Entschlüsselung versprechen, auf jedem Gerät und im Netz laufen und außerdem für Authentifikation und digitales Signieren taugen. Im Prinzip sollen sie wie die aktuellen asymmetrischen Public-Key-Verfahren funktionieren, nur zusätzlich 'quantenfest' sein.

Seit 2016 wurden zunächst 50, inzwischen wohl knapp 70 Vorschläge gesammelt, wovon nach umfangreichen Tests 2022 zunächst drei, nach zusätzlichen Vorschlägen inzwischen (September 2024) wohl wieder vier aussichtsreiche Kandidaten für eine amerikanische bzw. internationale Standardisierung übrig geblieben sind. Ein zunächst vielversprechender Kandidat namens SIKE schied 2022 überraschend aus, nachdem eine damit angeblich sogar quantensicher verschlüsselte Nachricht innerhalb einer Stunde mit einem einfachen Laptop geknackt werden konnte (vgl. heise-Bericht).

Auch wenn noch keine Entscheidung über ein weltweit einzusetzenden Verfahren gefallen ist, versprechen wohl einige Firmen ihren Kunden jetzt schon quantensichere Kryptografie (wie it-daily.net berichtet, u.a. auch ein VPN-Anbieter, der mit dem Versprechen von Ewigkeitsschutz die interne Kommunikation von Firmen dauerhaft vor Fremden verbergen möchte). Auch Messengerdienste, etwa Signal, experimentieren angeblich schon mit eigenen Hybridsystemen. Dass jedenfalls schon jetzt etwas getan werden muss, weiss auch die Neue Züricher Zeitung und mahnt in einem Artikel!

Auf jeden Fall sind z.B. Softwareentwickler und vor allem Hersteller längerlebiger Gebrauchsgüter (etwa von Hausinstallationen oder von selbstfahrenden Autos) gut beraten, nur noch modular aufgebaute Hard- und Software zu verwenden, wo das Verschlüsselungsverfahren gekapselt und unabhängig vom Rest austauschbar ist. Vorläufig kann ein z.Z. noch sicheres und gängiges Verfahren oder schon einer der bisher aussichtsreichen Post-Quanten-Kandidaten implementiert werden; später braucht dann nur ein leicht zugänglicher Chip ausgetauscht oder ein Software-Update aufgespielt werden, um auf ein besseres Verfahren oder eine kommende Norm umzustellen. So nennt etwa der TÜV viele wichtige Anwendungsbereiche und will seinen Firmenkunden helfen, schon jetzt Produkte und Abläufe auf den zukunftssicheren Schutz von Informationen auszurichten -- und dient sich dabei als externer Berater an.

Und Privatleute? Auch sie sollten doppelt vorsichtig sein, welche Nachrichten sie in verschlüsselten Chats versenden oder welche persönlichen Daten sie in der Cloud speichern (bewusst oder automatisch durch Backups/Synchronisation ihres Handys oder PCs) -- selbst bei seriösen Diensten, die nach heutigem Standard Ende-zu-Ende-Verschlüsselung anbieten und versprechen, dass auch sie selbst als Betreiber die anvertrauten Informationen nicht lesen können, weil sie höchstens den Public Key kennen, während der Private Key beim Absender bleibt. Voraussichtlich kann der geheime Private Key in ein paar Jahren mit Quantencomputern leicht ermittelt werden, sodass der heutige Schutz dann leicht aushebelbar wird und die Informationen plötzlich praktisch offen lesbar, frei zugänglich oder zumindest von Datenbrokern zu kaufen sind...

Zusatz/Ergänzung Oktober 2014: Über das Prinzip, sechs verschiedene technische Umsetzungen, Ziele und aktuelle Fortschritte beim Bau von Quantencomputern informiert sehr schön der Artikel "Quantencomputer -- Wettkampf der Qubits" in Spektrum der Wissenschaft, Heft 10.24, Seiten 12 bis 23 (leider kostenpflichtig). Eine Tabelle verschiedener Bauformen zeigt all-electronics in "Diese Arten von Quantencomputern gibt es". Informativ und noch aktuell ist der Grundlagen-Artikel "So funktioniert ein Quantencomputer" von der Quarks-Wissenschaftsredaktion.

zum Seitenanfang / zum Seitenende

zurück zur Informatik-Hauptseite

zurück zur ersten Kryptologie-Seite

weiter zur nächsten Seite 'Schutz der Programmieridee durch (Krypto-)Obfuscation'

(Die anderen Java-Seiten werden am besten auf der Informatik-Hauptseite ausgewählt)

zum Anfang dieser Seite

Willkommen/Übersicht  -  Was ist neu?  -  Software  -  Mathematik  -  Physik  -  Informatik  -   Schule: Lessing-Gymnasium und -Berufskolleg  -  Fotovoltaik  -  & mehr  -  Kontakt: e-Mail,  News-Abo, Gästebuch, Impressum  -  Grußkarten, site map, Download und Suche

Diese Seite ist Teil des Webangebots  http://www.r-krell.de